теория цифровых автоматов. курсовая-Теория цифровых автоматов. Курсовая работа по курсу Теория цифровых автоматов

• Название: Курсовая работа по курсу Теория цифровых автоматов
• Анкор: теория цифровых автоматов
• Дата: 14.10.2021
• Размер: 0.74 Mb.
• Имя файла: курсовая-Теория цифровых автоматов.doc
• Тип: Курсовая; #247746
• страница: 2 из 4

1.2 Элемент

Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B)

Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
Таблица

a	b	A+b
0 1 0 1	0 0 1 1	0 1 1 1

«1» тогда и только тогда, когда хотя бы на одном входе действует «1»,

«0» тогда и только тогда, когда на всех входах действуют «0»



Рис.
.3 JK -триггер

Триггер работает так же как RS-триггер, с одним лишь исключением: при подаче логической единицы на оба входа J и K состояние выхода триггера изменяется на противоположное. Вход J (от англ. Jump - прыжок) аналогичен входу S у RS-триггера. Вход K (от англ. Kill - убить) аналогичен входу R у RS-триггера. При подаче единицы на вход J и нуля на вход K выходное состояние триггера становится равным логической единице. А при подаче единицы на вход K и нуля на вход J выходное состояние триггера становится равным логическому нулю. JK-триггер в отличие от RS-триггера не имеет запрещённых состояний на основных входах, однако это никак не помогает при нарушении правил разработки логических схем. На практике применяются только синхронные JK-триггеры, то есть состояния основных входов J и K учитываются только в момент тактирования, например по положительному фронту импульса на входе синхронизации.

На базе JK-триггера возможно построить D-триггер или Т-триггер. Как можно видеть в таблице истинности JK-триггера, он переходит в инверсное состояние каждый раз при одновременной подаче на входы J и K логической 1. Это свойство позволяет создать на базе JK-триггера Т-триггер, объединив входы J и К.

Алгоритм функционирования JK-триггера можно представить формулой

Таблица

J	K	Q(t)	Q(t+1)
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1

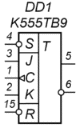Рис.

2. Теоретические основы построения цифровых автоматов

2.1 Общие положения

Термин «автомат», как правило, используется в двух аспектах. С одной стороны, автомат - устройство, выполняющее некоторые функции без непосредственного участия человека. В этом смысле мы говорим, что ЭВМ - автомат, так как после загрузки программы и исходных данных ЭВМ решает заданную задачу без участия человека. С другой стороны, термин «автомат» как математическое понятие обозначает математическую модель реальных технических автоматов. В этом аспекте автомат представляется как «черный ящик», имеющий конечное число входов и выходов и некоторое множество внутренних состояний, в которые он под воздействием входных сигналов переходит скачкообразно, т.е. практически мгновенно, минуя промежуточные состояния. В действительности это условие не выполняется, так как любой переходный процесс длится конечное время.

Автомат называется конечным, если множество его внутренних состояний и множество значений входных сигналов - конечные множества.

В практике часто используется понятие цифрового автомата, пот которым понимают устройство, предназначенное для преобразования цифровой информации. Входные сигналы в цифровых автоматах представляются в виде конечного множества мгновенных сигналов. Теоретически это означает, что входные сигналы не имеют длительности, хотя практически это не так. Все события должны относится к фиксированному времени t, поэтому такое допущение упрощает рассмотрение процессов, происходящих в автоматах. Условно также принимается, что число выходных сигналов y(t) конечно. И они возникают вследствие действия входных сигналов. Одновременно с появлением выходного сигнала меняется (скачкообразно) внутреннее состояние автомата.

Цифровой автомат называется правильным, если выходной сигнал определяется его внутренним состоянием (на данный или предыдущий момент времени) и не зависит от входных сигналов.

Понятие состояние автомата используется для описания систем, выходы которых зависят не только от входных сигналов в данный момент времени, но и от некоторой предыстории, т.е. сигналов, поступивших на входы системы ранее. Состояние автомата соответствует некоторой памяти о прошлом, позволяя устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов.

В цифровых автоматах помимо логических элементов имеются элементы памяти. Элементы памяти используются для того, чтобы фиксировать предыдущее состояние автомата. В качестве элементов памяти могут использоваться триггеры. Каждое внутреннее состояние цифрового автомата определяется исходным состоянием триггеров и последовательностью входных сигналов, действующих на входе в данный момент времени. Поэтому такие устройства называются последовательностными схемами. К последовательностным схемам можно отнести: триггеры, счетчики, регистры. В общем случае структурная схема цифрового автомата может быть представлена в виде набора трех узлов: комбинационной схемы формирования выходных сигналов, комбинационной схемы формирования сигналов управления триггерами и собственно памяти (рис. 2).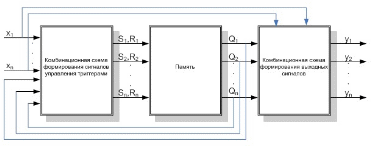


Рисунок 2. Управляющее устройство со схемной логикой.

На вход комбинационной схемы управления триггерами поступают комбинации входных сигналов x₁, х₂, ... , x_к, комбинации сигналов, отражающих состояние элементов памяти Q₁, Q₃, ... , Q_m. С учетом этих множеств комбинационная схема формирует серии сигналов, управляющих состояниями триггеров. Кодовые комбинации из состояний триггеров образуют внутренние состояния цифрового автомата, которые принято обозначать буквой a.

Комбинационная схема формирования выходных сигналов формирует сигналы y₁, у₂.....у_Р. Они могут использоваться для управления какими-либо узлами, для активизации процессов в других схемах. Эти сигналы могут зависеть только от внутренних состояний - в этом случае устройство следует называть автоматом Мура. А если выходные сигналы зависят и от входных сигналов, то автоматом Мили.

Таким образом, для задания цифрового автомата необходимы три множества:

множество входных сигналов: x₁, х₂, ... , x_к;

множество выходных сигналов: y₁, у₂.....у_Р;

множество внутренних состояний: a₁, a₃, ... , a_z.

На указанных трех множествах задают две функции: функцию переходов и функцию выходов.

Последовательность действий автомата по формированию выходных сигналов и сигналов управления триггерами с учетом входных сигналов может быть задана с помощью алгоритма. Алгоритм фактически является формализованным представлением задачи по построению цифрового устройства, где определены группы выходных сигналов для инициализации устройств схемы (например, операционного устройства процессора) в зависимости от поступления тех или иных входных сигналов (х). Задавать цифровой автомат удобно с помощью графа. Графом называется непустое конечное множество узлов (вершин) вместе с множеством дуг (ветвей), соединяющих пары различных узлов. Граф обычно представляется в наглядной форме, при этом вершины изображаются точками или кругами, которые помечаются с целью идентификации, а ветви изображаются линиями, соединяющими соответствующе узлы. Если каждой дуге также приписало направление, то такой граф называется ориентированным. Если направления не указаны, то граф называется неориентированным. Данные представления полезны ввиду их наглядности. Вершины обычно соответствуют объектам некоторого вида (в цифровом автомате - внутренним состояниям), а дуги - физическим или логическим связям между ними. Таким образом, графы можно использовать для математического моделирования самых разнообразных систем и структур: электрических схем, вычислительных сетей и т.д.