квазиклассическая теория рассеяния(распеч). Курсовая работа по теме Квазиклассическая теория рассеяния. Исполнитель Студент 4 курса
 Скачать 307 Kb. Скачать 307 Kb.
|
|
Министерство высшего образования Воронежский государственный университет Физический факультет Курсовая работа по теме: ‘’Квазиклассическая теория рассеяния.’’ Исполнитель: Студент 4 курса Крисилов А. 1.Квазиклассичкская теория рассеяния. В случае когда взаимодействие нельзя считать малым и рассматривать как возмущение борновское приближение неприменимо. Но если при этом велика скорость частиц, то возможно использование квазиклассического приближения. Рассмотрим решение интегрального уравнения Шрёдингера 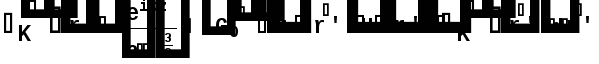 где Считаем, что при больших скоростях большинство частиц пролетают, не испытывая влияния потенциала. Будем искать волновую функцию в виде 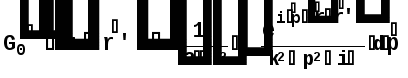 Уравнение Шрёдингера примет вид 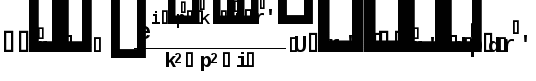  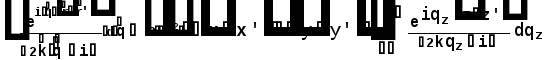   Решением этого интегрального уравнения является функция 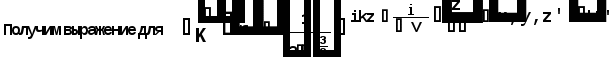  Получанное приближение называется приближением эйконала(о - образ), оносоответствует приближению геометрической оптики. Полученная волновая функция не удовлетворяет ассимптотическому условию, но это не влияет на величину амплитуды рассеяния f() , так как в области, где V(r)0 она передаёт поведение истинной волновой функции, а её свойства на больших расстояниях несущественны. 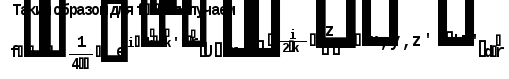 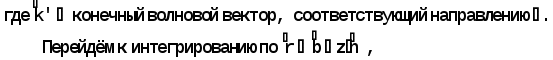  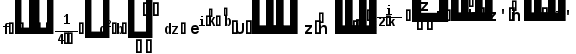 Интеграл по dz' вычисляется 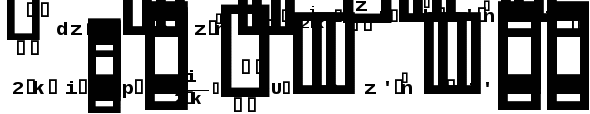 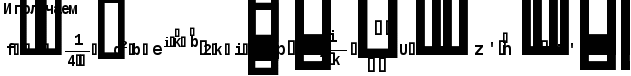 Если разложить экспоненту в ряд и ограничиться первым неисчезающим слагаемым, то получится амплитуда рассеяния в 1 борновском приближении : 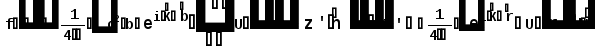 Амплитуду рассеяния в приближении эйконала также можно выразить через функцию Бесселя нулевого порядка : 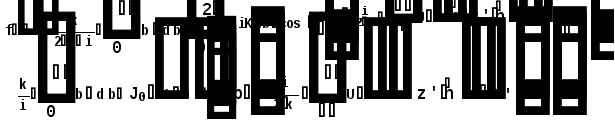 2.Оптическая теорема. Оптическая теорема связывает интегральное сечение рассеяния с амплитудой расскеяния вперёд. (k,b) - комплексная функция,так как потенциал U может иметь мнимую часть, учитывающую поглощение частиц. 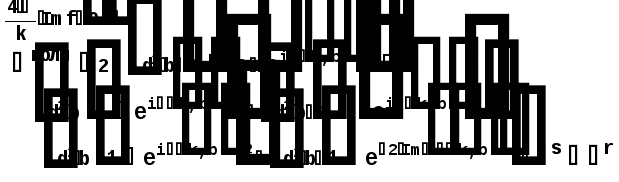 первое слагаемое соответствует рассеянию ,а второе-поглощению частиц. Рассмотрим в качестве примера рассеяние на непрозрачном шаре радиуса a . 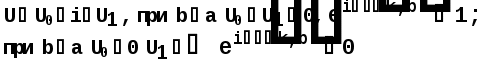 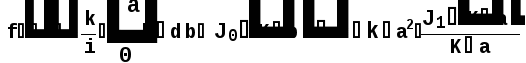 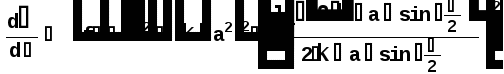 что соответствует картине дифракции классических волн. 3.Метод фаз рассеяния . Исключив из рассмотрения угол =0, так как иначе сечение расходится, для амплитуды рассеяния существует выражение 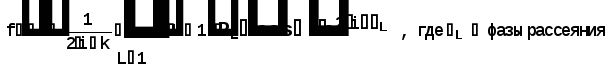 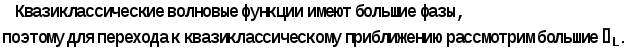 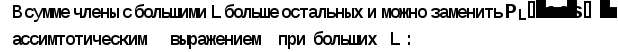 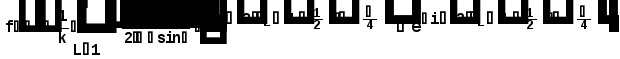 Экспоненциальные множители быстро осциллируют, и в сумме взаимно уничтижаются члены со всеми L ,кроме области значений L ,в которой показатели экспоненты имеют экстремум.Условие экстремума имеет вид : 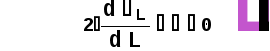   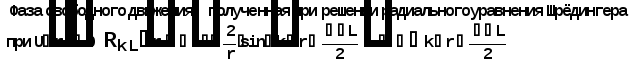 Фаза рассеяния равна разности фаз движения в поле и свободного движения   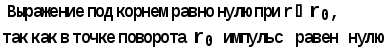 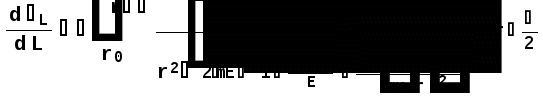 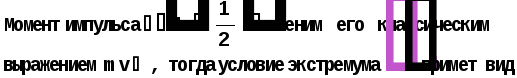 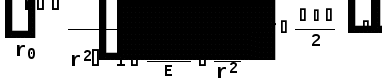 Знак "-" соответствует отталкиванию, Знак "+" - притяжению. Уравнение (**) в точности совподает с классическим уравнением, определяющим угол рассеяния по прицельному параметру.  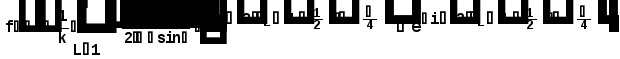 Суммирование по L заменим интегрированием по dL'вблизи точки L'=0 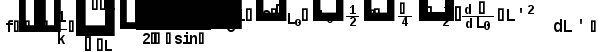  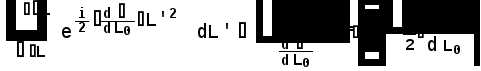  В итоге получаем для амплитуды рассеяния 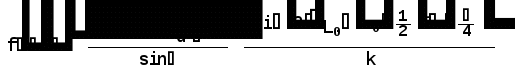 И для сечения рассеяния : 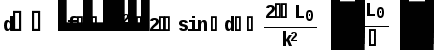 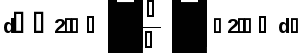 При этом условие квазиклассичности примет вид при заданном  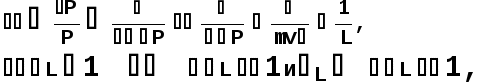 Получим условие квазиклассичности для потенциала : 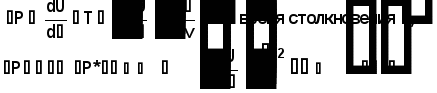 Условие квазиклассичности должно выполняьтся ко всей классически доступной области |U(r)| 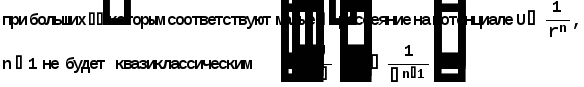  |
