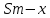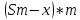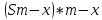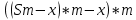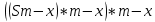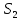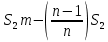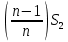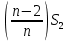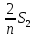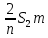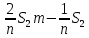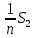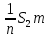задания на рулетке. Рулетка 5. Решение Пусть
 Скачать 140.58 Kb. Скачать 140.58 Kb.
|
  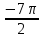  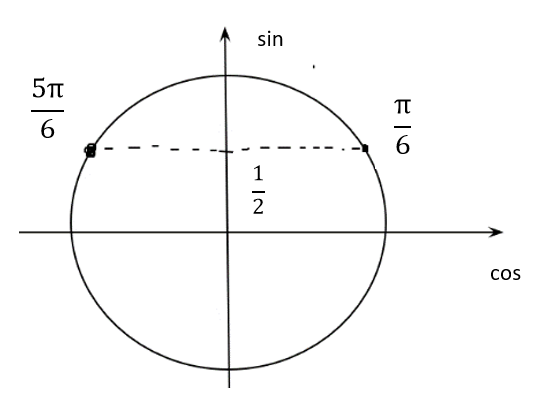 Вспомним основное тригонометрическое тождество 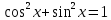 Распишем второе слагаемое через синус  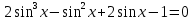 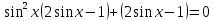 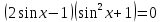 | |  Так, как Так, как  Разделим на скобочку, которая не равна 0 Разделим на скобочку, которая не равна 0 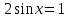 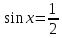   б) Выполним отбор корней с помощью тригонометрической окружности 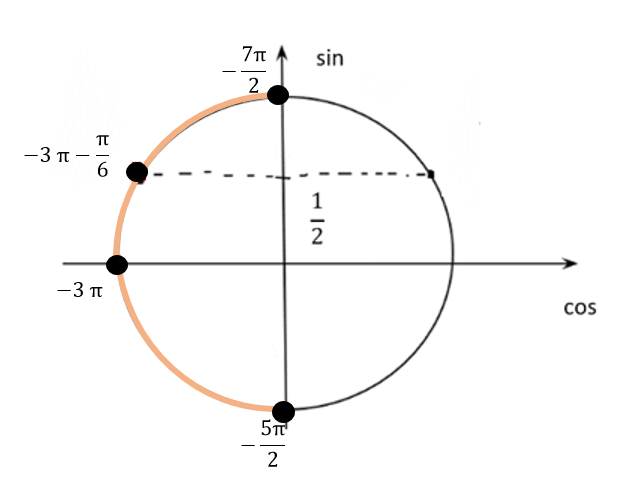 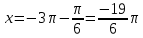 Ответ: а)  б) б)  Подсказки: 1) Распиши  через основное тригонометрическое тождество через основное тригонометрическое тождество2) Приведи подобные слагаемые и группируем первое со вторым и третье с четвёртым слагаемым 14. Смешанные экономические задачи 14-го декабря 2020 года Андрей планирует оформить кредит в банке размером в 1 090 000 рублей на 52 месяца. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 4% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга, причем первые три платежа – равные; — 15-го числа каждого месяца, начиная c марта 2021 года, долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что сумма первых трех выплат составила 693 300 рублей. Найдите сумму всех выплат. 1 702 700 рублей Решение: Пусть S  сумма кредита сумма кредита  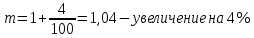
Известно, что сумма первых трех выплат составила 693 300 рублей Тогда 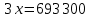 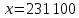 Вычислим долг на начало 4 месяца он будет равен долгу после выплат в третьем месяце 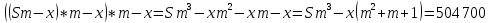 рублей рублейПусть 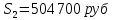 Теперь начиная с 4 месяца существования нашего кредита долг будет уменьшаться на одну и ту же сумму 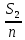 , где , где  – оставшийся срок – оставшийся срок 
Запишем сумму выплат с 4 по 52 месяц 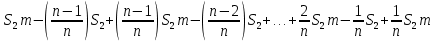 Вынесем за скобочку из выражений со знаком плюс “ Вынесем за скобочку из выражений со знаком плюс “ 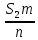 ” а из тех, что с минусом - “ ” а из тех, что с минусом - “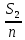 ” уммум 52 месяц ту же сумму енования нашего кредита долг будет умешьшаться на одну и туже ” уммум 52 месяц ту же сумму енования нашего кредита долг будет умешьшаться на одну и туже Получим  Заметим, что внутри скобочек арифметическая прогрессия Тогда запишем её сумму для  и и 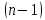 элементов элементовВыражение примет вид:  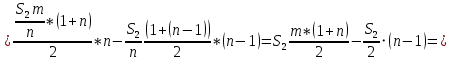  руб. руб.Учтём первые три платежа, и получим, что сумма всех выплат равна 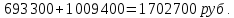 |