курсовая онх. Курсовач. копммммя. Курсовая работа по теме Методы сравнительного расчёта М. Х. Карапетьянца

• Название: Курсовая работа по теме Методы сравнительного расчёта М. Х. Карапетьянца
• Анкор: курсовая онх
• Дата: 24.05.2021
• Размер: 46.24 Kb.
• Имя файла: Курсовач. копммммя.docx
• Тип: Курсовая; #209321

Российский химико-технологический университет имени Д. И. Менделеева

Кафедра общей и неорганической химии

Курсовая работа по теме:

«Методы сравнительного расчёта М. Х. Карапетьянца».

Выполнил: студент Кузнецов М.С.

группа П-18

Проверил: профессор Бушуев Н. Н.

Москва,2019 г

Задача №457

Постройте график линейной зависимости у=а+bx и на его основе, используя, таким образом, один из методов сравнительного расчёта М. Х. Карапетьянца, определить энтальпию (энергию) кристаллической решетки Н_кр фторида натрия NaF ,если известны значения Н_кр, кДж/моль, для кристаллических фторидов и хлоридов щелочных металлов.

у(Hкр)	1041,3	826,5	804,8	752,7	?
х(Hкр)	857	714,7	695,3	669,1	785,3

Решение:

Способ №1: Для нахождения функции, описывающей усредняющую линию зависимости энтальпии кристаллической решетки элемента, используем систему, применяемую в методе наименьших квадратов: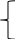

ax_i² + bx = x _iy_i

ax_i + bn = y_i

Введём обозначения:

Х = Hкр – известные значения

У = Hкр – неизвестное значение

Решив данную систему с помощью метода Гаусса, используя программу Microsoft Excel , найдём значения а и b:

a = 1.511

h= - 252.67

Функция усредняющей линии задаётся уравнением y=ax+b , поэтому получаем:

Y=1.511x-252.67

Подставив данное значение Х=785,3, получим У=933,794

Поэтому у=Hкр(NaF) = 933.794 кДж/моль

Способ №2: Наиболее простым способом решения этой задачи является использование функции «Тенденция» в программе Excel. Она возвращает значения значения в соответсвии с линейным трендом, аппроксимириуя прямой линией (по методу наименьших квадратов) массивы «известные значения_у» и «известные значения_х». Функция возвращает значения у, соответствующие этой прямой для заданного массива «новые значения_х»



В данном способе ввод: «ТЕНДЕНЦИЯ (B3:E3;B4:E4;F4;ИСТИНА)»

в любую ячейку, например, F3 в программе Excel сразу даст ответ: 933,794, то есть аналогично предыдущему способу:

у=Hкр(NaF) = 933.794 кДж/моль

Задача №458

Постройте график линейной зависимости у=а+bx и на его основе, используя, таким образом, один из методов сравнительного расчёта М. Х. Карапетьянца, определить энтальпию (энергию) кристаллической решетки Н_кр RbBr , если известны значения Н_кр, кДж/моль для кристаллических фторидов и хлоридов рубидия и калия.

у(Hкр)	804,8	695,3	629,7	?
х(Hкр)	826,5	714,7	647,5	684

Решение:

Способ №1: Ф-ция «Тенденция» Microsoft Excel позволяет наиболее быстро получить нужное значение: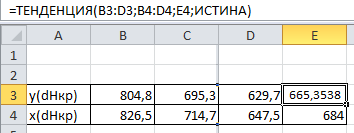

В ячейке E3 получено значение при помощи данной функции.

Изобразим полученную усредняющую прямую и отметим известные и полученные значения Н_кр:

2 способ: Для нахождения функции, описывающей усредняющую линию зависимости энтальпии кристаллической решетки элемента, используем систему, применяемую в методе наименьших квадратов: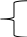

ax_i² + bx = x _iy_i

ax_i + bn = y_i

Введём обозначения:

Х = Hкр – известные значения

У = Hкр – неизвестное значение

Решив данную систему с помощью метода Гаусса, используя программу Microsoft Excel , найдём значения а и b:

a=0.97834

b=-3.827

Функция усредняющей линии задаётся уравнением y=ax+b , поэтому получаем:

Y=0.97834x-3.827

Подставив данное значение Х=684, получим У= 665.3538. Поэтому у=Hкр(RbBr) = 665.3538 кДж/моль

Вывод к работе

В задаче №457 мы определили энтальпию (энергию) кристаллической решетки Н_кр фторида натрия NaF и нашли уравнение зависимости энергии кристаллической решетки фторидов щелочных металлов от энергий кристаллических решеток хлоридов этих же металлов. Для этого нам были даны энергии кристаллических решеток хлоридов щелочных металлов. Также был использован периодический закон Д. И. Менделеева, повествующий о периодическом изменении свойств элементов.

Стандартной молярной энтальпией кристаллической решетки называется изменение энтальпии, которым сопровождается образование одного моля твердого ионного соединения из входящих в него ионов в их газообразном состоянии при стандартных условиях. Это табличные величины ,установленные эмпирически.

Для расчёта энтальпии кристаллической решетки использовался метод наименьших квадратов. Задача была решена несколькими способами:

Первый способ заключался в нахождении уравнения усредняющей линии с помощью системы уравнений:

ax_i² + bx = x _iy_i

ax_i + bn = y_i

С помощью метода Гаусса находим a и b.Данные значения дают нам функции y=ax+b, используя которую мы и находим нужное нам значение.

Второй способ заключался в построении графика зависимости энтальпии кристаллических решеток фторидов щелочных металлов от энтальпии кристаллических решеток хлоридов тех же металлов. Данный график был построен при помощи функции «Тенденция» в Microsoft Excel: она возвращает значения в соответствии с линейным трендом, аппроксимируя прямой линией (по МНК). Это является самым простым и быстрым способом решения данной задачи.

Одинаковый ответ, полученный двумя способами, говорит об идентичности способов и правильности ответа.

В задаче 458 нужно было найти энтальпию кристаллической решётки RbBr. Для этого были даны стандартные энтальпии кристаллических решёток галогенидов калия и рубидия. Эта задача была решена также двумя способами, которые дали идентичные ответы. В итоге можно сделать вывод , что на ответ способ решения не влияет. Применение МНК в химии базируется на периодическом законе Д.И.Менделеева.