дррщр. Курсовая по ТОЭ Исследование линейной цепи в переходных и устано. Курсовая работа по теоретическим основам электротехники
 Скачать 1.46 Mb. Скачать 1.46 Mb.
|
Санкт-Петербург 2004г. СодержаниеЗадание к курсовой работе……………………………………………………………………………………………3 Нормировка параметров цепи…………………………………………………………………………………………4 Анализ цепи во временной области методом переменных состояния при постоянных воздействиях………………………………………………4 Анализ цепи операторным методом при апериодическом воздействии……………………………………………………………………………………………………………………8 Качественный анализ цепи частотным методом при апериодическом воздействии……………………………………………………………………………11 Анализ цепи частотным методом при периодическом Воздействии……………………………………………………………………………………………………………………15 Вывод…………………………………………………………………………………………………………………………………………………19 Список использованной литературы…………………………………………………………………………20 ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ Анализ цепи во временной области методом переменных состояния при постоянных воздействиях; Анализ цепи операторным методом при апериодическом воздействии; Качественный анализ цепи частотным методом при апериодическом воздействии; Анализ цепи частотным методом при периодическом воздействии.   НОРМИРОВКА ПАРАМЕТРОВ ЦЕПИ Далее индекс «*» опускается Анализ цепи во временной области методом переменных состояния при постоянных воздействиях Составление уравнений состояния цепи для Сведем динамическую цепь к резистивной (заменим С-элемент источником напряжения, а L-элемент заменим на источник тока):  Выразим переменные состояния (ic и UL), используя метод узловых напряжений  Определяем коэффициенты: После подстановки численных значений получаем: Все переменные выражаем через переменные состояния и воздействия: 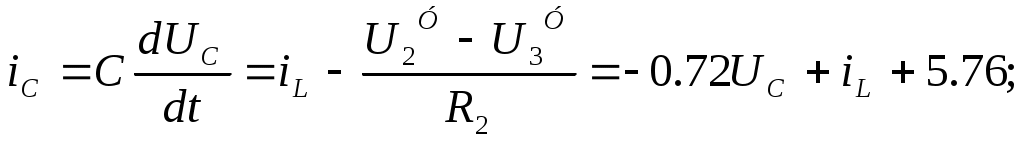 Уравнения состояния цепи: Нахождение точных решений уравнений состояния Общий вид решений уравнений состояния: Независимые начальные условия    Определяем вынужденные составляющие при Определяем корни характеристического многочлена Определяем постоянные интегрирования Точное решение уравнений состояния: Построение точных решений уравнений состояния:   Анализ цепи операторным методом при апериодическом воздействии Операторная схема замещения:   Определение функции передачи Применим метод пропорциональных величин для нахождения функции передачи Функция передачи: Нахождение нулей и полюсов функции передачи и нанесение их на плоскость комплексной частоты Конечных нулей функция передачи не имеет;  Определение из функции передачи переходной импульсная характеристика Обратное преобразование Лапласа: переходная характеристика Обратное преобразование Лапласа: Определение изображения по Лапласу входного одиночного импульса Получим изображение сигнала путем дифференцирования    Для получения самого сигнала, дважды проинтегрируем Определение тока  Построение графиков переходной и импульсной характеристик цепи, а также входного и выходного сигналов   Качественный анализ цепи частотным методом при апериодическом воздействии Нахождение и построение амплитудно-фазовой (АФХ), амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристик функции передачи цепи АЧХ: ФЧХ:  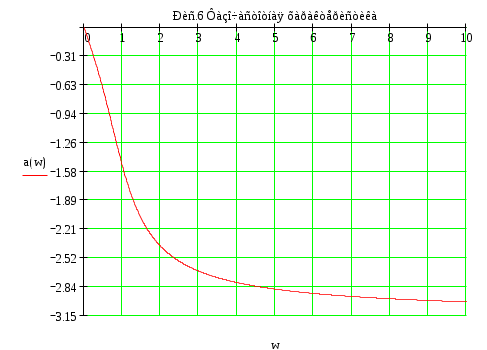  Определение полосы пропускания цепи по уровню Полоса пропускания определена по графику Нахождение и построение амплитудного и фазового спектров апериодического входного сигнала и определение ширины спектра по уровню  Комплексный спектр входного сигнала:  Приведем выражение в скобках к синусу по Эйлеру (умножим и разделим на 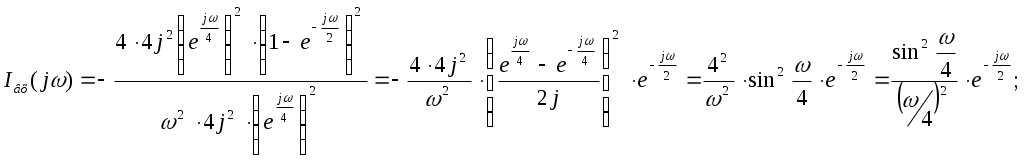 Амплитудный спектр входного сигнала: Амплитудный спектр входного сигнала: 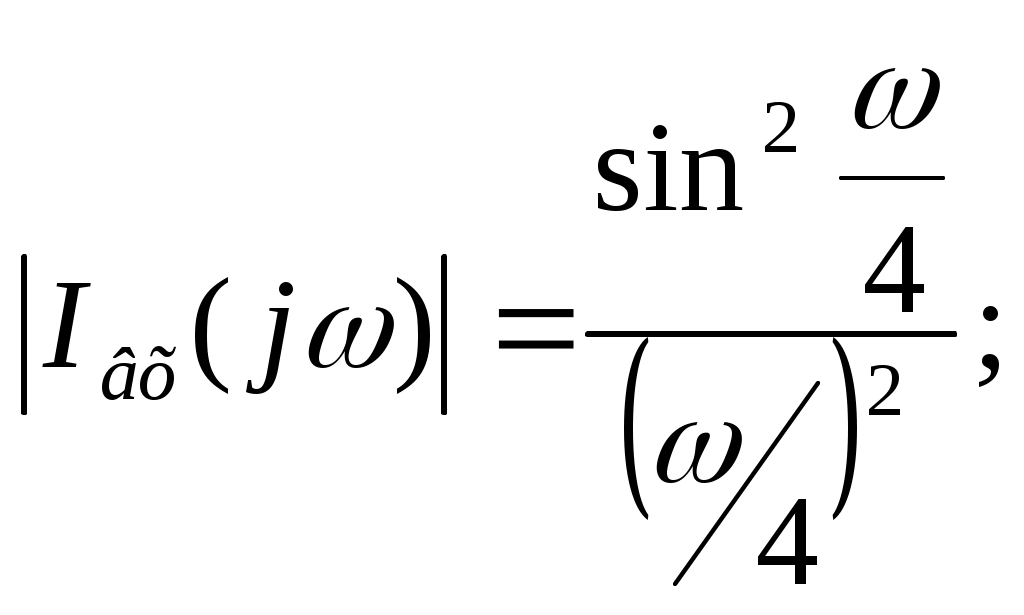 Фазовый спектр входного сигнала:   Ширина спектра определяется по графику: Сопоставляя соответственно спектры входного сигнала с частотными характеристиками цепи, дадим заключение об ожидаемых искажениях сигнала на выходе цепи. Можно установить, что приблизительно одна десятая часть амплитудного спектра входного сигнала укладывается в полосу пропускания, а фазочастотная характеристика в этой полосе имеет гиперболическую зависимость, в отличие от прямолинейной фазочастотной характеристики входного сигнала. Таким образом, при прохождении через цепь входной сигнал будет в значительной степени искажен. На выходе цепи можно ожидать сигнал, значительно более слабый, чем поданный на вход, и более выраженный по своей продолжительности. Этот качественный вывод подтверждается точным расчетом в п.2 (см. Рис.4) Анализ цепи частотным методом при периодическом воздействии Разложим в ряд Фурье заданный входной периодический сигнал. Построим его амплитудный и фазовый спектры.    Для получения амплитудного и фазового дискретного спектра выделим модуль и фазу, для этого выражение сведем к синусу по Эйлеру (умножим и разделим на  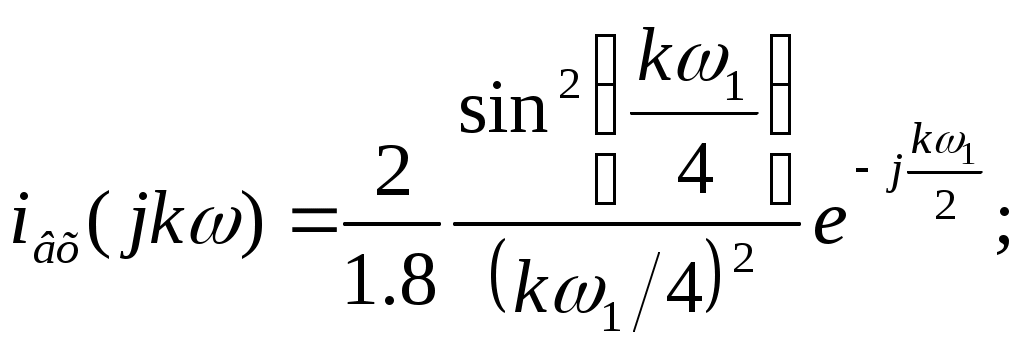 Амплитудный дискретный спектр:  Фазовый дискретный спектр:
  Построение входного периодического сигнала и его аппроксимации отрезком ряда Фурье Число гармоник ряда Фурье определяется шириной спектра по уровню  Построение амплитудного и фазового спектров выходного периодического сигнала, используя рассчитанные в п.3.1 АЧХ и ФЧХ функции передачи цепи. Запись тока АЧХ: ФЧХ:    Амплитуды и начальные фазы гармоник выходного напряжения:
  В соответствии с принятым критерием ширины спектра: Построение графика тока   ВЫВОД: При исследовании линейной цепи, можно сделать заключение, что при прохождении треугольного импульса через цепь он искажается: растягивается во времени, изменяется его амплитуда. На выходе при периодическом воздействии импульса получены слабовыраженные колебания тока. Список использованной литературы Матханов П. Н. Основы анализа электрических цепей. Линейные цепи. - М.: Высш. школа, 1990. Матханов П. Н. Основы анализа электрических цепей. Нелинейные цепи. - М.: Высш. школа, 1986. Бычков Ю.А., Золотницкий В.М., Чернышев Э.П. Теория электрических цепей. Переходные процессы. Установившейся синусоидальный режим: Учеб. Пособие для самостоятельной работы \ ГЭТУ. СПб., 1993 Башарин С.А., Бычков Ю.А. Компьютерное моделирование и расчет электрических цепей \ Учеб. Пособие \ ГЭТУ. СПб., 1994 Ю.А. Бычкова, Э.П. Чернышева Курсовое проектирование по теории электрических цепей: Учеб. Пособие для самостоятельной работы студентов. ГЭТУ. СПб., 1996 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
