Курсовая работа построить обход шахматной доски конем, так, чтобы на каждом поле побывать ровно 1 раз

• Название: Курсовая работа построить обход шахматной доски конем, так, чтобы на каждом поле побывать ровно 1 раз
• Анкор: rehcjdfz
• Дата: 18.12.2021
• Размер: 0.77 Mb.
• Имя файла: Kursovaya_Lunin_KI20-02-1b.docx
• Тип: Курсовая; #308236

Федеральное государственное автономное

образовательное учреждение

высшего образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Институт космических и информационных технологий

Кафедра прикладной математики и компьютерной безопасности


КУРСОВАЯ РАБОТА
Построить обход шахматной доски конем, так, чтобы на каждом поле побывать ровно 1 раз.

Руководитель _________ Богульская Н.А.

подпись, дата инициалы, фамилия
Студент КИ20-02/1б _________ Лунин И.В

номер группы, зачетной книжки подпись, дата инициалы, фамилия

Красноярск 2021

Содержание

1. 
   Постановка задачи…………………………………………… ……………..3
   
2. 
   Обзор алгоритмов ……………..…………………………………………....4
   
3. 
   Оценка сложности алгоритма……………….…………………………………………………….8
   
4. 
   Код программы оптимального алгоритма………………..……………………………………………………9
   
5. 
   Заключение…………………………………………………………………..13
   
6. 
   Список используемых источников………………………….……………..14
   

Постановка задачи

Построить обход шахматной доски конем, так, чтобы на каждом поле побывать ровно 1 раз.

Провести сравнение вычислительной сложности известных алгоритмов для

решения задачи. Выделить основные методы решения задачи о ходе коня, классифицировать и сравнить эти методы.

Обзор алгоритмов

Рассмотрим итеративные методы решения данной задачи:

Метод Мунка и Коллини.

Шахматную доску разделим па две части: внутреннюю, состоящую из 16 полей, и внешнюю, имеющую форму рамы и состоящую из 48 полей. На полях внутреннего квадрата запишем заглавные буквы А, В, С, D - так, чтобы каждая из них, повторенная четыре раза, образовала квадрат, по всем сторонам которого может ходить конь. Аналогичные (строчные) буквы запишем на рамочных полях так, чтобы ходы коня по каждой из букв образовали замкнутые многоугольники вокруг центрального квадрата.


Конь начинает ходить от какого-нибудь рамочного поля внешнего квадрата, предварительно выбрав строчную букву. За 12 ходов исчерпывает эту букву (Последнее поле не должно быть угловым). Затем он переходит во внутренний квадрат выбирая заглавную букву. Пройдя все поля, обозначенные этой буквой, конь снова переходит на раму - на букву, по которой еще не ходил, и вновь совершает 12 ходов. Алгоритм повторяется пока все поля не будут задеты фигурой.

Метод Полиньяка и Роже

Разделим доску крестом на четыре квадрата. В каждом из них расставим буквы а, b, с, d .



Конь начинает движение с любой буквы, проходит в выбранном квадрате по всем четырем полям с этой буквой, затем переходит на ту же букву соседнего квадрата, и т. д. Исчерпав все 16 полей с одной буквой, он меняет ее и снова зигзагом обегает доску. После четырех таких кругов все поля будут пройдены. После окончания алгоритма конь не должен встать в угловое поле.

Метод Эйлера

М етод Эйлера заключается в том, что конь двигается по произвольному маршруту, пока не исчерпает все возможные ходы. Далее оставшиеся непройденными клетки добавляются в сделанный маршрут, после специальной перестановки его элементов.

Метод Вандермонда

В основе метода лежит возможность замены обратными всех ходов, начиная с поля, связанного ходом коня с конечным.

Вандермонд свел задачу к арифметической. Суть метода заключается в обозначении маршрута коня в виде последовательности дробей x/y, где x и y (где x и y координаты поля на доске). В соответствии с ходами коня разность числителей двух дробей будет равно 1 или

Кроме того, числитель и знаменатель не могут быть меньше 1 и больше 8.

Метод нахождения подходящей последовательности аналогичен методу Эйлера, но находит маршруты коня только для досок чётной размерности.
Рекурсивный метод:

Правило Варнсдорфа является разновидностью жадного алгоритма

1) при обходе доски коня следует всякий раз ставить на поле, из которого он может сделать наименьшее число ходов на еще не пройденные поля;

2) если таких полей несколько, то разрешается выбирать любое из них.



D- алгоритм хода коня

Так как подход Варнсдорфа допускает произвольные размеры доски представим рекурсивную функцию для данного варианта.

Пусть D зафиксировано и на шахматной доске размером n*n в позиции (x, y) находится конь. Составить рекурсивную программу-функцию, находящую D-алгоритмом обход доски конем, если он существует. При отсутствии обхода должна быть выдана “тупиковая позиция” - матрица-доска с уже зафиксированным неполным обходом.




ClockW(n, x, y) - это размер доски (n) и начальная точка (x, y), с которой начинается перемещение коня.

1. 
   ClockW() инициируется нулями доска-матрица H размером n*n и осуществляется первый ход.
   
2. 
   Реализуется обращение к рекурсивной функции Vans()
   
3. 
   После вычислений выводится матрица H с полным или неполным туром коня. В последнем случае непройденные поля остаются помеченными нулями.
   

Vans(n, x, y, H, j) - это размер доски (n), точка (x, y), с которой осуществляется очередной ход коня, доска (H) и глубина рекурсивных обращений (j). Функция Vans() возвращает текущее состояние матрицы.

(Используемая в Vans() константа D – это матрица приращений для формирования очередного хода коня.)

Просчет по программе ClockW(n, x, y) позволяет найти обходы доски 8*8 с каждого из 64 её полей.

Матрица D для формирования ходов коня

и разрешения неопределенных ситуаций при n = 8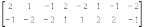

Оценка сложности алгоритма

В качестве рационального решения данной задачи был выбран алгоритм Варнсдорфа. Преимущества данного алгоритма:

1. 
   Обладает гибкостью по сравнению с другими алгоритмами, так как может быть использован для доски произвольных размеров. Исходя из общих замечаний «… программа должна допускать произвольные значения размерности задачи. Возможны только ограничения, которые указываете в отчете, например n<1 000 000».  
   
2. 
   Отладка рекурсивного алгоритма проще чем итеративного.
   
3. 
   Рекурсия хорошо подходит для реализации алгоритмов обхода комбинаторных задач.
   

Диапазон сложности алгоритма: O(N²) до O(64*N ²)(При отсутствии возвратов). Данная характеристика показывает полиномиальный рост. На каждом шаге выбирается правильный ход. Это позволяет достичь максимальной скорости выполнения алгоритма. Тесты данного алгоритма показали средний результат сложности в O(25*N ²).

Код программы оптимального алгоритма

#include "stdafx.h"

#include

#include

#include

#include

#include

#include
using namespace std;

int n = 1, x, y, sx, sy, i,

xx[] = { 2,1,2,-2,-1,-1,-1,-2 }, yy[] = { -1,-2,1,1,-2,2,2,-1 };

int xnext, ynext;

int maxDeskSize;

void print();

int refund;// переменная показывающая "ошибки"

int iteration = 0; // количество возвратов из рекурсии

int desk[8][8]; // поля доски

int nstep; // № шага

int tupik(int curx, int cury, int* freeField);

void inputData();

void Path(int x0, int y0);

int step(int x0, int y0)

{

if (iteration > 1000000)

{

return 0;

}

if (x0 < 0 || x0 >n - 1 || y0 < 0 || y0 >n - 1) return 0; // выход за пределы доски

if (desk[y0][x0] != 0) return 0; // пройденое поле

desk[y0][x0] = nstep++;// отмечает свободное поле

if (nstep > n * n) return 1; // все поля отмечены => успех
int prior[9];

for (int i = 0; i < 9; i++)

prior[i] = 0;

refund = tupik(x0, y0, prior);

if (refund != -1)

{

if (refund == 2)

return 1;//успешно нашли выход

for (int i = 1; i < 9; i++)

{

for (int j = 0; j < 8; j++)

{

if (prior[j] == i)

{

if (step(x0 + xx[j], y0 + yy[j])) return 1;// поиск успешного хода

}

}

}

}

nstep--; // вернуться на ход назад

iteration++;

desk[x0][y0] = 0; // стереть отметку поля

return 0; // последовательность не найдена

}
int tupik(int curx, int cury, int* freeField)

{

//freeField - массив хранящий индексы по ходу с минимальным количеством исходящих полей

for (i = 0; i < 8; i++) {

x = curx + xx[i];

y = cury + yy[i];

if (x >= n || x < 0 || y < 0 || y >= n) continue;

if (nstep == n * n && desk[y][x] == 0)

{

desk[y][x] = nstep++;

return 2;//нашли последнее поле, пора выходить

}

if (!desk[y][x]) {

for (int j = 0; j < 8; j++) {

xnext = x + xx[j];

ynext = y + yy[j];

if (xnext >= n || xnext < 0 || ynext < 0 || ynext >= n) continue;

if (desk[ynext][xnext] == 0)

freeField[i]++;

}

}

}
for (int i = 0; i < 8; i++)

{

if (freeField[i] != 0)

{

return 1;//получили массив с количеством ходов из каждой возможной клетки

}

}

return -1;//тупик

}
int _tmain(int argc, _TCHAR* argv[])

{

setlocale(LC_ALL, "Russian");

inputData();

freopen("output.txt", "w", stdout);

Path(sx, sy);

if (iteration > 1000000)

{

cout << "Путь не найдет или ошибка";

return 0;

}

print();

cout << "Подведение итогов возвращения назадk\n";

cout << "________________\n";

printf("%-8d", iteration);

cout << "\n________________\n";

cout << "\n";

return 0;

}
void Path(int x0, int y0)

{

for (int i = 0; i < n; i++)

for (int j = 0; j < n; j++)

desk[i][j] = 0; // очистка доски

nstep = 1; // установить номер шага

step(x0, y0); // вызвать функцию для исходной позиции

}
void inputData()

{

setlocale(LC_ALL, "Russian");

do

{

if (n > 59 || n < 1)

{

cout << "Повторите ";

}

else cout << "Укажите размер доски";

scanf("%d", &n);//размерность шахматной доски

} while (n > 59 || n < 1);
do

{

if (sx < 0 || sx >= n || sy < 0 || sy >= n)

{

cout << "Повторите: X:";

cin >> sx;

}

else

{

cout << "Вход начините координаты: X:";

cin >> sx;

}

cout << "Y:";

cin >> sy;

sx--; sy--;

} while (sx < 0 || sx >= n || sy < 0 || sy >= n);

}

void print()

{

for (int i = 0; i < n; i++)

{

for (int j = 0; j < n; j++)

{

printf("%-3d ", desk[i][j]);

}

cout << endl;

}

cout << endl; cout << endl;

}

Пояснение по работы программы

Программа просит ввести:

1.Размер шахматного поля;

2.Стартовую клетку расположения коня на шахматном поле;

3.На выходе получаем квадратную матрицу заданной размерности, в каждой клетке которой будет написан номер хода, которым конь попадает туда из стартовой клетки.

*Выходные данные записываются в файл. Если со стартовой клетки невозможно обойти все поле, то в файле запишется сообщение о невозможности такого обхода.

Заключение

К одному из наиболее интересных разделов программирования относятся задачи из области искусственного интеллекта, в которых решение ищется методом "проб и ошибок". При этом имеет место перебор при поиске решения, продолжительность которого может быть сокращена за счет применения тех или иных эвристических правил — методов оптимизации.
Мы исследовали одну из наиболее известных задач этого класса — задачу о ходе коня. В ходе исследования этой задачи требовалось найти и сравнить алгоритмы решения и программно реализовать один из методов.
Был произведен анализ алгоритмов и выявлено четыре основных алгоритма решения: Мунка и Коллин, Полиньяка и Роже, метод Эйлера, метод Вандермонда , правило Варнсдорфа.

Все методы разделены на две группы. Первая группа – итеративны, эта группа включает методы: Мунка и Коллин, Полиньяка и Роже, Эйлера, Вандермонда:. Вторая группа – рекурсивный, к таким методам относятся Правило Варнсдорфа.

Список используемых источников

Интернет ресурсы:

https://ru.wikipedia.org/wiki/Задача_о_ходе_коня

https://habr.com/ru/post/78728/

Литература:

1. 
   Стивен С. Скиена. Алгоритмы Руководство по разработке (2-е издание)
   
2. 
   Бобак И. Алгоритмы: "возврат назад" и "разделяй и властвуй" //Программист. 2002. №3.
   
3. 
   Гарднер М. Математические новеллы. М.: Мир, 1974.
   
4. 
   Гик Е. Шахматы и математика. М.: Наука, 1983.
   
5. 
   Шалыто А.А., Туккель Н.И. Реализация автоматов при программировании событийных систем //Программист. 2002. №4.