курсовая. Курсовая Гаджиева Ханпашы12. Курсовая работа признаки равномерной сходимости функциональных рядов по дисциплине математический анализ
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
|
Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «Дагестанский государственный университет» Факультет математики и компьютерных наук Кафедра математического анализа КУРСОВАЯ РАБОТА Признаки равномерной сходимости функциональных рядов по дисциплине математический анализ Выполнил: студент 2 курса очной формы обучения по направлению 02.03.01 – Математика и Компьютерная наука Гаджиев Ханпаша Шамилович Научный руководитель: Кандидат физ-матем. наук Шарапудинов Тимур Идрисович Работа допущена к защите: МАХАЧКАЛА 2022   Содержание Введение…………………………………………………………... 5 Глава 1. Теоретическая часть……………………………………. 6 Равномерная сходимость функционального ряда………….. 6 Свойства равномерно сходящихся рядов …………………... 7 1.3 Признаки равномерно сходящихся рядов………………....... 8 Глава 2. Практическая часть…………………………………..... 14 2.1 Примеры. Признак Вейерштрасса………………………….. 14 2.2 Примеры. Признак Лейбница………………………………. 19 2.3 Пример. Признак Абеля…………………………………….. 20 Заключение………………………………………………………. 21 Список литературы……………………………………………… 22 Введение Математика является наукой, которая широко используются на практике. Любой производственно-технологический процесс не обходится без фундаментальных математических закономерностей. Зачастую идеи и методы, созданные для решения частных задач, принимают общий характер и требуют строгого обоснования. Те методы, которые выдержали всесторонние проверки и весьма длительные испытания, впоследствии становятся математическими теориями. В дальнейшем эти теории используются при решении более широкого круга задач, нежели те, на основе которых они были созданы. Инженерная практика в значительной мере ориентирует и стимулирует развитие математического аппарата. Именно потому, что элементы математики встречаются на производстве практически на каждом шагу, специалистам важно знать и блестяще ориентироваться в области применения тех или иных инструментов анализа и расчета. Основные положения теории функциональных рядов являются важнейшей составляющей математической подготовки студентов инженерных, экономических и других специальностей. Вопросы сходимости и суммируемости рядов, представления функций рядами остаются актуальными в современной математической науке, ее приложениях, находят применения в таких учебных курсах, как дифференциальные уравнения, комплексный анализ, теория вероятностей, вычислительная математика и др. В данной курсовой работе были разобраны много примеров признаков равномерной сходимости функциональных рядов, такие как признак Вейерштрасса, Абеля, Дирихле, критерий Коши и т.д Глава 1. Теоретическая часть Равномерная сходимость функционального ряда. 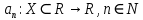 Определение 1. Ряд вида 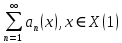 называется функциональным рядом. Определение 2. Множество 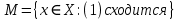 называется областью сходимости ряда (1). Сходимость ряда (1) эквивалентна сходимости функциональной последовательности его частичных сумм называется областью сходимости ряда (1). Сходимость ряда (1) эквивалентна сходимости функциональной последовательности его частичных сумм 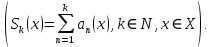 Определение 3. Говорят, что ряд (1) сходится равномерно на M, если последовательность 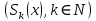 сходится равномерно на M. сходится равномерно на M.Замечание. Если 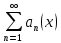 сходится равномерно на M, то сходится равномерно на M, то 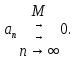 Пример. 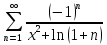 сходится равномерно на 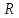 . .Доказательство. Так как 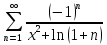 – ряд Лейбница, то – ряд Лейбница, то 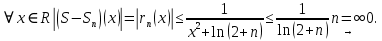 Поэтому Поэтому 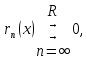 что доказывает равномерную сходимость ряда что доказывает равномерную сходимость ряда 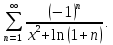 Пример. 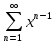 не сходится равномерно на (-1,1). Доказательство. Предположим, что 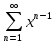 сходится равномерно на (-1,1). Тогда сходится равномерно на (-1,1). Тогда 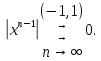 Но это не верно, так как Но это не верно, так как 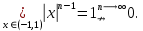 Пример. 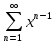 сходится равномерно на 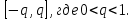 Доказательство. 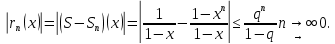 Теорема 4. (Критерий Коши равномерной сходимости ряда). 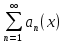 сходится равномерно на сходится равномерно на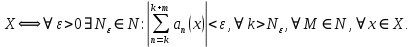 1.2. Свойства равномерно сходящихся рядов. Теорема 5. Пусть 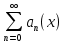 сходится равномерно на 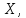 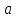 – предельная точка – предельная точка 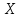 и пусть и пусть 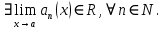 Тогда Тогда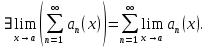 Теорема 6. Пусть  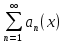 сходится равномерно на 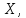 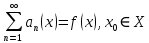 и пусть и пусть 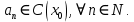 Тогда Тогда 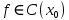 . .Замечание. Из того, что  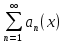 сходится на 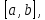 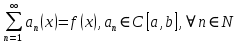 и и 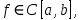 вообще говоря, не следует, что ряд вообще говоря, не следует, что ряд 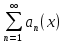 сходится на сходится на 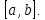 Пример. 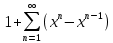 не сходится равномерно на (-1,1). Доказательство. 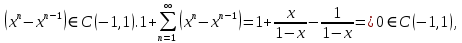 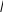 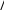 но сходимость ряда не равномерна. В самом деле, 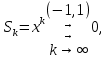 так как так как 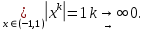 Теорема 7. Пусть 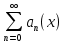 сходится равномерно на сходится равномерно на 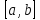 и и 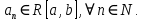 Тогда Тогда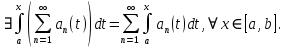 Теорема 8. Пусть 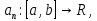 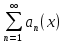 сходится в некоторой точке сходится в некоторой точке 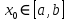 , пусть для всякого , пусть для всякого 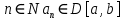 и пусть и пусть 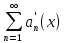 сходится равномерно на сходится равномерно на 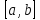 . Тогда . Тогда 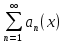 сходится равномерно на сходится равномерно на 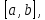 причем причем 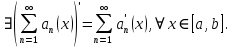 1.3. Признаки равномерной сходимости рядов Теорема 9 (Признак Вейерштрасса). Пусть 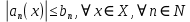 и и 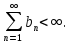 Тогда Тогда 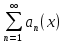 сходится абсолютно и равномерно на сходится абсолютно и равномерно на 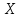 . .Доказательство. Пусть 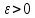 – произвольно. Тогда – произвольно. Тогда 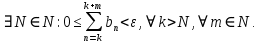 Следовательно, Следовательно,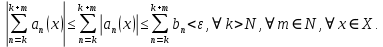 Рассмотрим пример непрерывной функции, не дифференцируемой ни в одной точке. 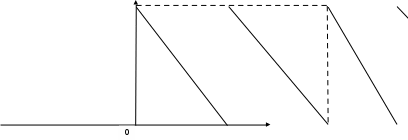 Пример (Ван-дер-Вардена). Рассмотрим функцию Пример (Ван-дер-Вардена). Рассмотрим функцию 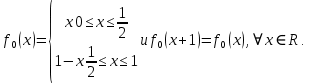  Определим теперь 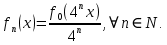 Тогда функция 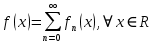 - искомая функция, то есть непрерывная и нигде не дифференцируемая. - искомая функция, то есть непрерывная и нигде не дифференцируемая.Доказательство. Так как, очевидно, 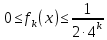 , ( , (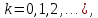 так что ряд мажорируется сходящейся прогрессией так что ряд мажорируется сходящейся прогрессией 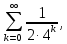 то по теореме 9 (Признак Вейерштрасса) ряд сходится равномерно, и функция то по теореме 9 (Признак Вейерштрасса) ряд сходится равномерно, и функция 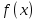 всюду непрерывна. всюду непрерывна.Остановимся на любом значении 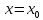 . Вычисляя его с точностью до . Вычисляя его с точностью до 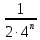 (где (где 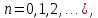 по недостатку и по избытку, мы заключим его между числами вида: по недостатку и по избытку, мы заключим его между числами вида: 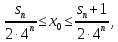 где где 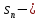 целое. Очевидно, что замкнутые промежутки целое. Очевидно, что замкнутые промежутки 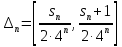 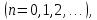 оказываются вложенными один в другой. В каждом из них найдется такая точка оказываются вложенными один в другой. В каждом из них найдется такая точка 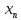 , что расстояние ее от точки , что расстояние ее от точки 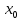 равно половине длины промежутка: равно половине длины промежутка: 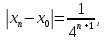 ясно, что с возрастанием ясно, что с возрастанием 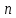 варианта варианта 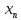 стремится к стремится к 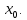 Составим теперь отношение приращений 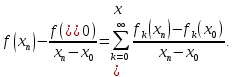 Но, при 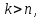 число число 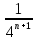 есть целое кратное периода есть целое кратное периода 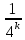 функции функции 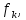 так что так что 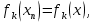 соответствующие члены ряда обращаются в 0 и могут быть опущены. Если же соответствующие члены ряда обращаются в 0 и могут быть опущены. Если же 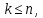 то функция то функция 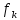 , линейная в промежутке , линейная в промежутке 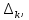 будет линейной и в содержащем ее промежутке будет линейной и в содержащем ее промежутке 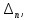 причем причем 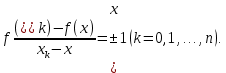 Таким образом, имеем окончательно 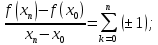 иными словами, это отношение равно четному целому числу при нечетном иными словами, это отношение равно четному целому числу при нечетном 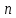 и нечетному целому при четном и нечетному целому при четном 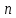 . Отсюда ясно, что при . Отсюда ясно, что при 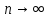 отношение приращений ни к какому конечному пределу стремиться не может, так что наша функция при отношение приращений ни к какому конечному пределу стремиться не может, так что наша функция при 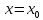 конечной производной не имеет. конечной производной не имеет.Лемма (Тождество Абеля). Пусть 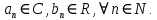 Обозначим Обозначим 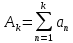 и и 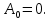 Тогда Тогда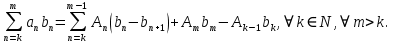 Теорема 10 (Признак Дирихле равномерной сходимости). Пусть 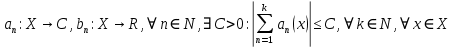 и пусть 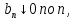 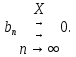 Тогда ряд Тогда ряд 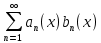 сходится равномерно на сходится равномерно на 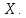 Доказательство. Имеем, 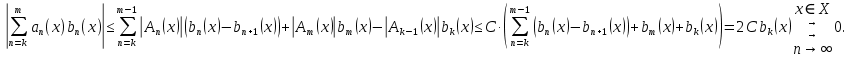 Следовательно, по теореме 4 (Критерий Коши равномерной сходимости ряда) 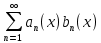 сходится равномерно. сходится равномерно.Пример. 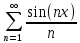 сходится равномерно на 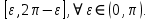 Доказательство. Имеем, 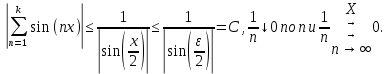 Пример. 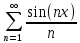 сходится, но не равномерно на 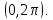 Доказательство. Пусть 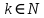 - произвольно. Выберем - произвольно. Выберем 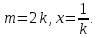 Тогда Тогда 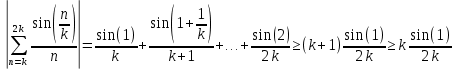 Имеем, 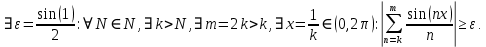 Теорема 11 (Признак Абеля равномерной сходимости). Пусть 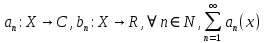 сходится равномерно на сходится равномерно на 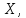 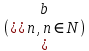 монотонна и равномерно ограничено константой монотонна и равномерно ограничено константой 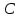 на на 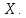 Тогда ряд Тогда ряд 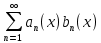 сходится равномерно на сходится равномерно на 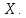 Доказательство. Пусть 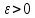 – произвольно. – произвольно.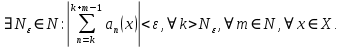 Для каждого фиксированного 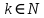 введем обозначения введем обозначения 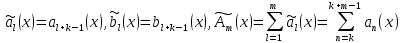 Имеем: 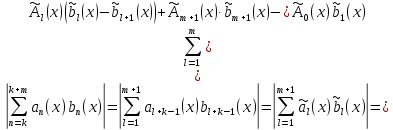 Глава 2. Практическая часть. 2.1 Примеры. Признак Вейерштрасса Признак Вейерштрасса. Если 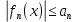 для любого для любого 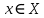 и ряд и ряд 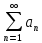 сходится, то ряд сходится, то ряд 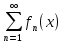 равномерно сходится. равномерно сходится.Итак для применения признака Вейерштрасса нужно оценить 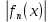 сверху через сверху через 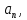 где где 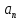 не зависит от не зависит от 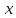 , причем числовой ряд , причем числовой ряд 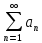 сходится. Заметим, что следующие условия равносильны: сходится. Заметим, что следующие условия равносильны:Существует такая последовательность 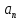 , что , что 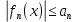 для каждого для каждого 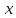 из из 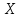 и каждого и каждого 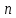 из из 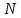 , причем ряд , причем ряд 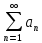 сходится; сходится;Ряд 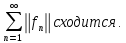 Импликация (1) 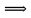 (2) получается из признака сравнения, а для доказательства импликации (2) (2) получается из признака сравнения, а для доказательства импликации (2)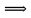 (1) достаточно положить (1) достаточно положить 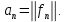 Таким образом, признак Вейерштрасса можно сформулировать по другому: Таким образом, признак Вейерштрасса можно сформулировать по другому:Признак Вейерштрасса. Если ряд 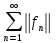 сходится, то ряд сходится, то ряд 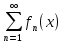 равномерно сходится. равномерно сходится.Ясно, что признаком Вейерштрасса можно пользоваться для исследования абсолютной равномерной сходимости (знакопеременного) функционального ряда, т.е. равномерной сходимости ряда 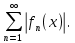 Пример 1. 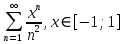 Решение. Заметим что 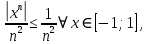 а числовой ряд 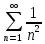 сходится. По признаку Вейерштрасса, функциональной ряд сходится. По признаку Вейерштрасса, функциональной ряд 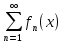 сходится равномерно. сходится равномерно.Пример 2. Пользуясь признаком Вейерштрасса, докажем равномерную сходимость функционального ряда 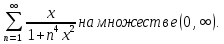 Найдем равномерную норму общего члена ряда, т.е. величину 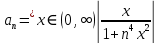 Для этого найдем производную и приравняем ее к нулю: 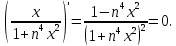 Отсюда 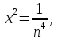 или или 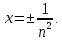 Ясно, что Ясно, что 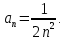 Поскольку ряд Поскольку ряд 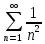 сходится, наш ряд сходится равномерно на сходится, наш ряд сходится равномерно на 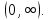 Пример 3. 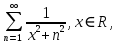 Решение. Заметим, что 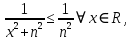 а числовой ряд 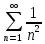 сходится. Следовательно, по признаку Вейерштрасса, функциональный ряд сходится. Следовательно, по признаку Вейерштрасса, функциональный ряд 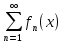 сходится равномерно. Для применения признака Вейерштрасса нужно знать некоторые неравенства. сходится равномерно. Для применения признака Вейерштрасса нужно знать некоторые неравенства. Пример. Доказать, что 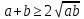 при любых при любых 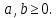 Решение. 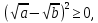 отсюда отсюда 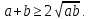 Пример 4. 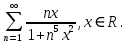 Решение. Заметим, что 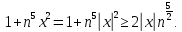 Отсюда Отсюда 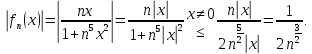 Итоговое неравенство 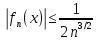 верно и при верно и при 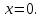 Показатель 3/2 больше 1, поэтому числовой ряд Показатель 3/2 больше 1, поэтому числовой ряд 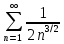 сходится. Функциональный ряд сходится. Функциональный ряд 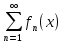 сходится равномерно по признаку Вейерштрасса. сходится равномерно по признаку Вейерштрасса.Пример. Доказать, что 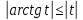 при любых при любых 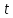 из из 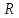 . .Решение. Из – за нечетности функций 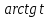 и и 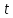 достаточно доказать неравенство при достаточно доказать неравенство при 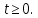 При таких При таких 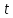 величины величины 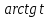 и и 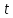 неотрицательны. Рассмотрим функцию неотрицательны. Рассмотрим функцию 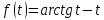 и найдем ее производную: и найдем ее производную: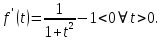 Функция 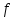 убывает на убывает на 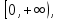 поэтому для любого поэтому для любого 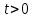 получаем, что получаем, что 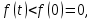 т.е. т.е. 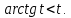 Пример 5. 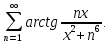 Решение. Воспользуемся ранее доказанными неравенствами: 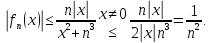 Окончательные неравенство 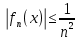 верно и при верно и при 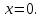 Числовой ряд Числовой ряд 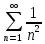 сходится. Поэтому функциональный ряд сходится. Поэтому функциональный ряд 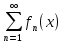 сходится равномерно по признаку Вейерштрасса. сходится равномерно по признаку Вейерштрасса.Пример 6. 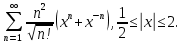 Решение. Оценим сверху выражение 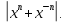 Это выражение четное , поэтому достаточно рассматривать при Это выражение четное , поэтому достаточно рассматривать при 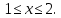 Первый способ (грубый) – оценить отдельно каждое слагаемое: 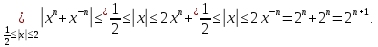 Точный способ – исследовать на монотонность при помощи производной и вычислить супремум: 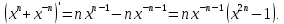 Максимум достигается в точках 2 и 1/2, равен 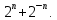 При При 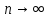 эта величина эквивалента эта величина эквивалента 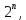 что в 2 раза меньше, чем при грубой оценке. Коэффициент 2 не меняет сходимости ряда, поэтому оставим грубую оценку что в 2 раза меньше, чем при грубой оценке. Коэффициент 2 не меняет сходимости ряда, поэтому оставим грубую оценку 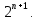 Получили неравенство Получили неравенство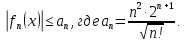 Рассмотрим ряд 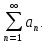 Из-за присутствия геометрической прогрессии и факториала его удобно исследовать с помощью признака Даламбера: Из-за присутствия геометрической прогрессии и факториала его удобно исследовать с помощью признака Даламбера: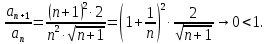 По признаку Даламбера, ряд 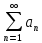 сходится. По признаку Вейерштрасса, ряд сходится. По признаку Вейерштрасса, ряд 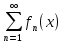 сходится равномерно. сходится равномерно.Пример 7. 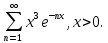 Решение. Пусть 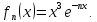 Нужно оценить эту величину сверху. Самая точная оценка – это супремум! Для исследования функции на экстремумы находим производную: Нужно оценить эту величину сверху. Самая точная оценка – это супремум! Для исследования функции на экстремумы находим производную: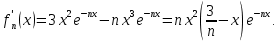 Отсюда видно, что максимум достигается в точке 3/n, 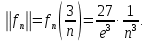 Ряд 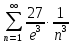 сходится. По признаку Вейерштрасса, функциональный ряд сходится. По признаку Вейерштрасса, функциональный ряд 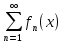 сходится равномерно. сходится равномерно.Пример 8. Доказать, что функциональный ряд сходится равномерно на промежутке 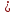 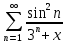 Доказательство. Для любого 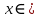 и для всех и для всех 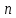 справедливо неравенство: справедливо неравенство: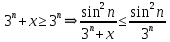 На рассматриваемом промежутке все члены функционального ряда неотрицательны, и поэтому знак модуля можно опустить. И поскольку 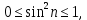 то: то: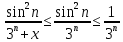 Таким образом, на полуинтервале 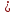 бесконечно убывающая геометрическая прогрессия бесконечно убывающая геометрическая прогрессия 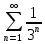 мажорирует функциональный ряд мажорирует функциональный ряд 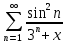 Следовательно, по признаку Вейерштрасса он равномерно сходится в данном промежутке. Что и требовалось доказать. Пример 9. Доказать, что функциональный ряд сходится равномерно на отрезке 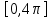 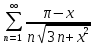 Доказательство. Преобразуем общий член ряда 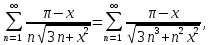 откуда становится понятно, что в качестве мажорантного ряда следует подбирать сходящийся ряд 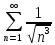 (возможно с множителем-константой). На отрезке (возможно с множителем-константой). На отрезке  функция функция  убывает от убывает от  до до  , поэтому , поэтому 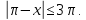 Таким образом, для любого Таким образом, для любого 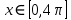 2.2 Примеры. Признак Лейбница Равномерной сходимости знакочередующихся функциональных рядов. Пусть при каждом 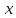 из из 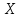 числовая последовательность числовая последовательность 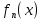 убывает и стремится к 0, и пусть убывает и стремится к 0, и пусть 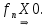 Тогда функциональный ряд Тогда функциональный ряд 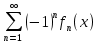 сходится равномерно. сходится равномерно.Доказательство. По признаку Лейбница для числовых рядов, при каждом 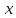 из из 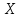 ряд сходится, причем ряд сходится, причем 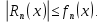 Поэтому Поэтому 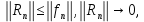 и ряд сходится равномерно. и ряд сходится равномерно.Пример 10. Исследовать ряд на равномерную сходимость: 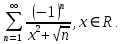 Решение. Пусть 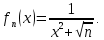 При каждом фиксированном При каждом фиксированном 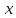 из из 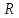 числовая последовательность числовая последовательность 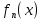 убывает и стремится к 0. Кроме того, убывает и стремится к 0. Кроме того, 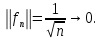 По признаку Лейбница для функциональных рядов, ряд сходится равномерно. Отметим, что в данном примере нельзя применить признаки Вейерштрасса: По признаку Лейбница для функциональных рядов, ряд сходится равномерно. Отметим, что в данном примере нельзя применить признаки Вейерштрасса: 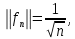 а ряд а ряд 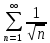 расходится. расходится.Пример 11. Исследовать сходимость функционального ряда 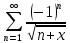 Решение. Прежде всего разберемся с областью определения, в данном случае подкоренное выражение должно быть строго положительным, и, кроме того, должны существовать все члены ряда, начиная с 1-го. Из этого следует то, что: 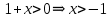 . При этих значениях получаются условно сходящиеся ряды: . При этих значениях получаются условно сходящиеся ряды: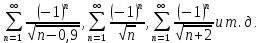 Другие же 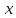 не годятся, так, например, при не годятся, так, например, при 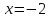 мы получим нелегальный случай мы получим нелегальный случай 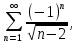 где не существует первых двух членов ряда. Я предлагаю схему, переход на числовые ряды. Рассмотрим произвольное значение где не существует первых двух членов ряда. Я предлагаю схему, переход на числовые ряды. Рассмотрим произвольное значение 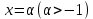 и исследуем сходимость числового ряда и исследуем сходимость числового ряда 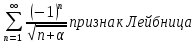 Данный ряд является знакочередующимся 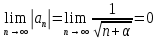 – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий : – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий : 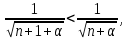 значит, убывание монотонно. значит, убывание монотонно.Вывод: ряд сходится по признаку Лейбница. Как уже отмечал, сходимость тут условная – по той причине , что ряд 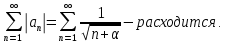 2.3 Пример. Признак Абеля Пример 1. Ряд 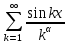 При 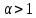 равномерно сходится на отрезке равномерно сходится на отрезке 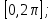 При 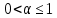 на любом отрезке на любом отрезке 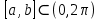 сходится равномерно; сходится равномерно;при 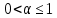 на любом отрезке на любом отрезке 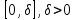 сходится, но не равномерно. сходится, но не равномерно.Покажем это. 1)При 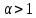 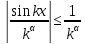 ряд ряд 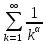 сходится. По признаку Вейерштрасса ряд сходится. По признаку Вейерштрасса ряд 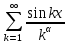 равномерно сходится на равномерно сходится на 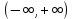 . .2) При 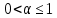 воспользуемся воспользуемся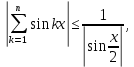 показывающей, что частичные суммы ряда 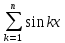 равномерно ограничены на каждом отрезке равномерно ограничены на каждом отрезке 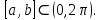 Числа же Числа же 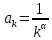 монотонно стремятся к нулю. По признаку Дирихле ряд монотонно стремятся к нулю. По признаку Дирихле ряд 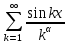 на каждом отрезке 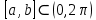 сходится равномерно. сходится равномерно.3) при 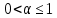 и любом и любом 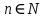 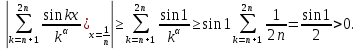 Следовательно, на отрезке 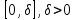 не выполняется условие Коши равномерной сходимости ряда не выполняется условие Коши равномерной сходимости ряда 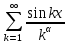 . По критерию Коши этот ряд не сходится равномерно. . По критерию Коши этот ряд не сходится равномерно.Заключение Итак, мы рассмотрели основные понятия функциональных рядов, вспомнили признаки сравнения рядов. Разобрали признаки Вейерштрасса, Дирихле, Абеля и критерий Коши. Выяснили как можно использовать данные признаки при решении задач. Из вышесказанного видно, что функциональные ряды тесно связаны со всеми разделами математики и другими науками. Функциональные ряды очень полезны в решении задач, которые обычными методами сложно или невозможно решить. Применение рядов встречается в таких сферах как: экономика, физика и других. Список литературы О.В.Бесов: Лекции по математическому анализу. Часть 1. — М.: МФТИ, 2004. — 325 с. Глава 16 Функциональные последовательности и ряды Математическая статистика: учебно-методическое пособие / авт.-сост. : С. Е. Демин, Е. Л. Демина ; М-во образования и науки РФ ; ФГАОУ ВО «УрФУ им. первого Президента России Б.Н.Ельцина», Нижнетагил. технол. ин-т (фил.). — Нижний Тагил : НТИ (филиал) УрФУ, 2016. — 284 с. Афонасенков О. В., Матвеева Т. А. Функциональные ряды, ряды и интеграл Фурье: Учеб. пособие / ВолгГТУ. – Волгоград, 2008. – 96 с. ISBN 5 – 230 – – Кудрявцев Л.Д. Курс математического анализа. Учеб. для вузов: В 3-х томах. – 5-е изд., перераб. и доп. –М.: Дрофа. Т.1. – 2003.-703 с. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Учеб. для вузов: в 3-х томах. – 8-е изд.-М.: Физматлит. т.1 – 2001. -697 с. Ильин В.А., Позняк Э.Г. Основы математического анализа. Учеб. для вузов в 2-х частях. – 6-е изд. стер. –М. Физматлит, 2002, -646 с. |
