расчет жб моста. Курсовая работа Проектирование городских мостовых сооружений
 Скачать 5.93 Mb. Скачать 5.93 Mb.
|
|
Расчет на прочность Расчет по нормальным напряжениям заключается в выполнении условия в крайних волокнах полки в сечении с максимальным моментом 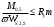 Где М0,5- Максимальный расчетный момент в сечений от первой части постоянной нагрузки 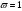 - коэффициент , учитывающий ограниченное развитие пластических деформаций в сечении - коэффициент , учитывающий ограниченное развитие пластических деформаций в сечении WS2,S - минимальный момент сопротивления Ry =347 - расчетное сопротивление для стали марки 10ХСНД. m=1 – коэффициент условий работы для автодорожных и городских мостов
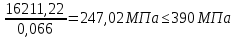 Условие прочности по нормальным напряжением выполняется. Значение касательных напряжений в сечениях стенок балок при М=0 (в опорном сечении) на уровне нейтральной оси должны удовлетворять условию 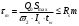 Где Q0 - максимальная поперечная сила в опорном сечении от первой части постоянной нагрузки Smax - статический момент полусечения Ix - момент инерции сечения относительно нейтральной оси tw- толщина стенки балки Rs - расчетное сопротивление на сдвиг 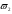 - коэффициент учитывающий неравномерное распределение напряжений по высоте значение которого определим по формуле - коэффициент учитывающий неравномерное распределение напряжений по высоте значение которого определим по формуле
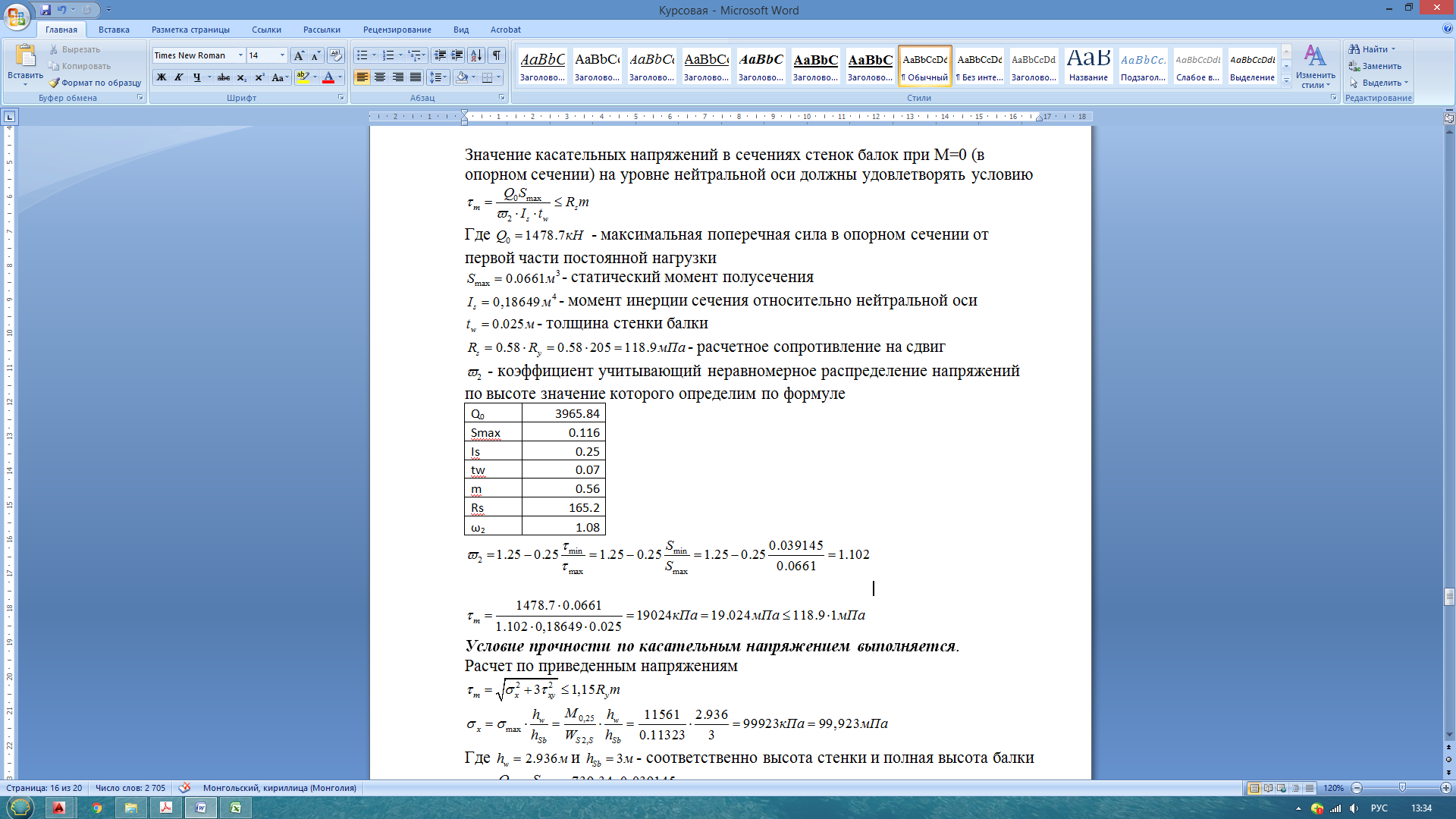  Условие прочности по касательным напряжением выполняется. Расчет по приведенным напряжениям 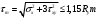  Где hw=2.01 и hSb=2.25 - соответственно высота стенки и полная высота балки.

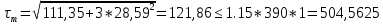 Условие прочности по приведенным напряжением выполняется. Расчет балки на устойчивость Приближенная (условная) проверка выполняется по формуле 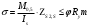
 - коэффициент продольного изгиба в зависимости от гибкости сжатого пояса - коэффициент продольного изгиба в зависимости от гибкости сжатого пояса 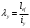  - расчетная длина сжатого пояса (расстояния между продольными связами), определяемая при отсутствии связей по сжатому поясу как расстояние между поперечными связами, при наличии связей – как расстояние между этими связами - расчетная длина сжатого пояса (расстояния между продольными связами), определяемая при отсутствии связей по сжатому поясу как расстояние между поперечными связами, при наличии связей – как расстояние между этими связами
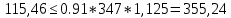 Условие устойчивости выполняется Расчет пролетного строения на 2 стадии работы На стадии 2 на балку передеается вторая часть постоянной нагрузки , состоящая из веса полотна проезжей части , веса тротуарной конструкции, барьерного и перильного ограждения, а также временная нагрузка. Усилия от этих нагрузок воспринимаются объединенным сечением. Геометрические характеристики сталежелезобетонного сечения Эффективную ширину железобетонной плиты bSl , которая будет учитываться в расчетах, определим согласно требованиям п.9.15 СП 35.13330.2011 , как сумму расчетных величин свесов плиты в обе стороны от оси стальной балки. Поскольку длина расчетного пролета lp=105м > 12C=12·1,25= 16 м То принимаем bc=1,25 м, C =1,25 м – ширина консоли плиты Поскольку lp=105 м > 4B = 4·1,25=5 м то b = 0,5·B =0,625 м Тогда эффективная ширина плиты составит bSl= 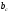 +b = 1,875 м +b = 1,875 м Толщина железобетонной плиты tst=0.2 м Коэффициент приведения 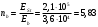 Здесь 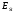 и и 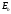 - модуль упругости стали и бетона класса В40 - модуль упругости стали и бетона класса В40 Расчетные формулы Площадь бетона плиты, вовлечённого в совместную работу со стальной балкой:
Площадь сталежелезобетонного сечения:
Статический момент объединенного сечения относительно центра тяжести стального сечения Сs:
Где а=1,08 - высота вута плиты Положение центра тяжести объединенного сечения Сstb: 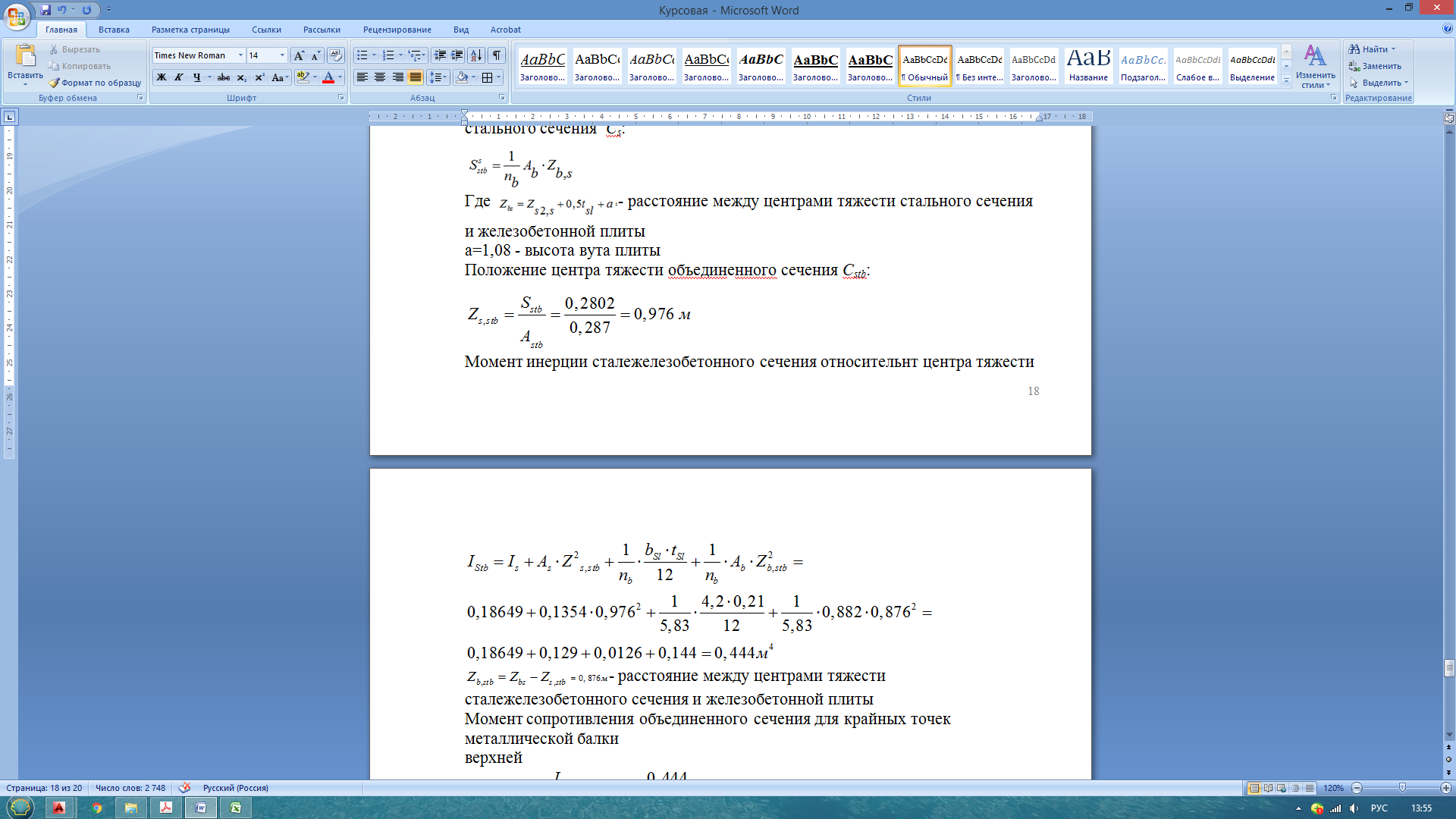
Момент инерции сталежелезобетонного сечения относительнт центра тяжести
Момент сопротивления объединенного сечения для крайних точек металлической балки верхней
Нижней
Момент сопротивления приведенного сечения для точки на уровне центра тяжести железобетонной плиты
Предварительная проверка прочности сечения балки по нормальным напряжениям Напряжения в верхнем и нижнем волокнах стальной балки на первой стадии работы 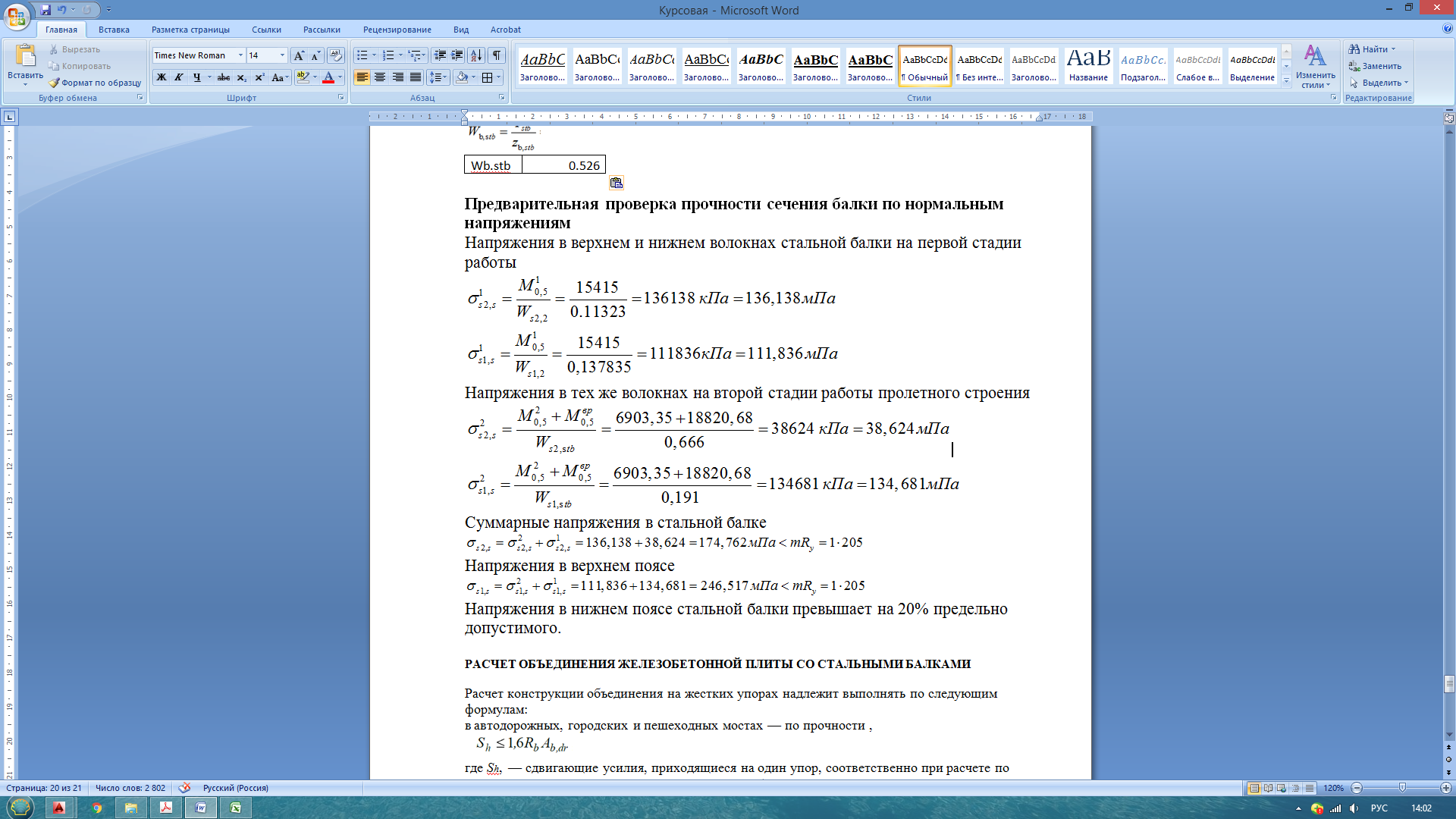 =123.51МПа =123.51МПа =80.84МПа =80.84МПаНапряжения в тех же волокнах на второй стадии работы пролетного строения  =79.48МПа =79.48МПа =155.28МПа =155.28МПаСуммарные напряжения в стальной балке 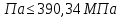 Напряжения в верхнем поясе  Проверки напряжений в верхнем поясе выполняются Напряжения в волокнах на уровне центра тяжести железобетонной плиты(сжатие): 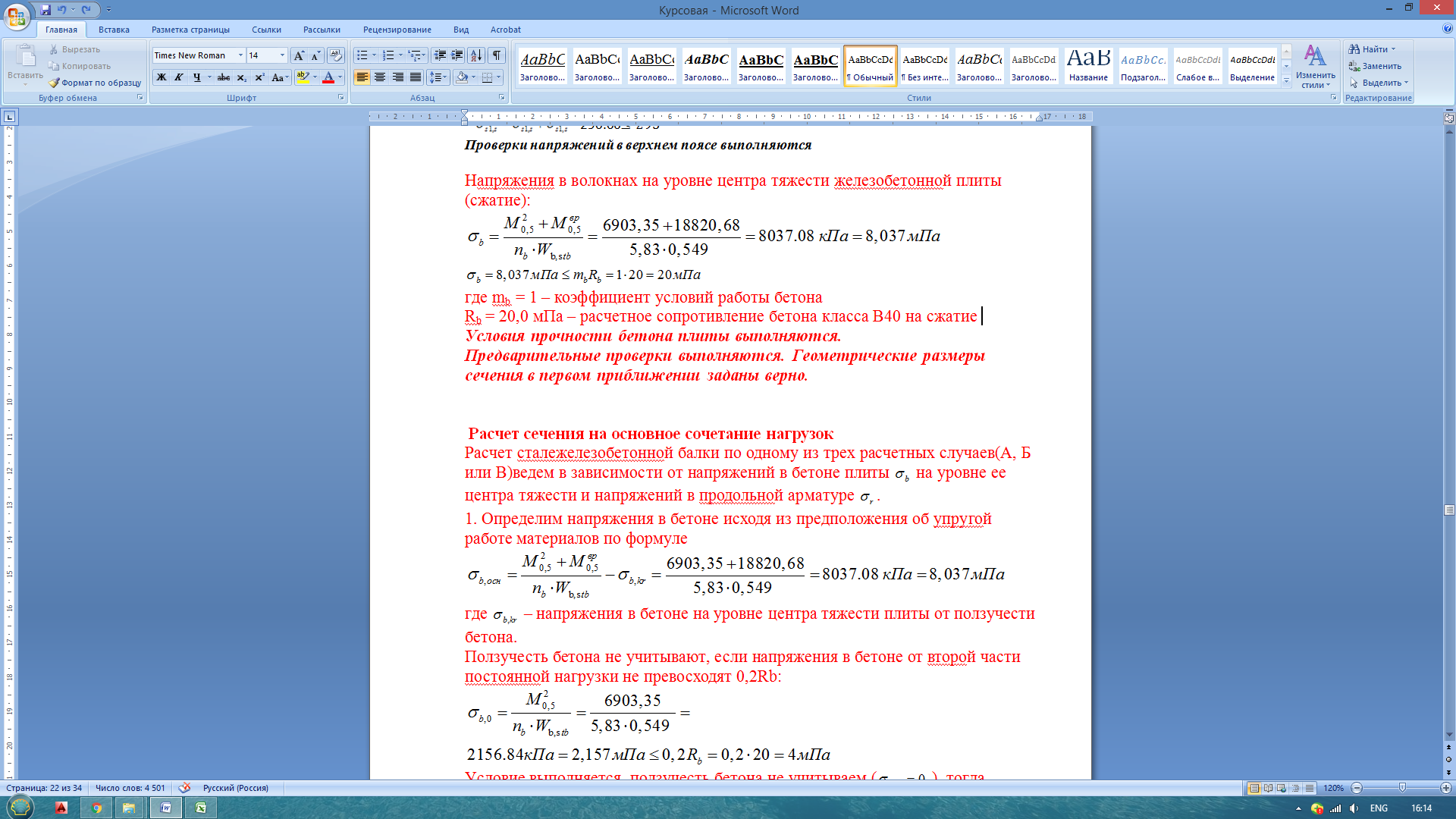
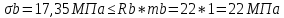 где mb = 1 – коэффициент условий работы бетона Rb = 22 МПа – расчетное сопротивление бетона класса В40 на сжатие Условия прочности бетона плиты выполняются. Предварительные проверки выполняются. Геометрические размеры сечения в первом приближении заданы верно. Расчет сечения на основное сочетания нагрузок Расчет сталежелезобетонной балки ведем в зависимости от напряжений в бетоне плиты 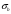 на уровне ее центра тяжести и напряжений в продольной арматуре на уровне ее центра тяжести и напряжений в продольной арматуре 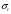 . .1. Определим напряжения в бетоне исходя из предположения об упругой работе материалов по формуле где 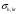 – напряжения в бетоне на уровне центра тяжести плиты от ползучести бетона. – напряжения в бетоне на уровне центра тяжести плиты от ползучести бетона.Ползучесть бетона не учитывают, если напряжения в бетоне от второй части постоянной нагрузки не превосходят 0,2Rb:
4,18<4,4, тогда σb,br=0 Условие выполняется, ползучесть бетона не учитываем ( 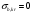 ), тогда ), тогда
2. Определяем напряжение в арматуре (сжатие – плюс, растяжение – минус):  Где  – модуль упругости арматуры; – модуль упругости арматуры; – напряжения в продольной арматуре от ползучести бетона. – напряжения в продольной арматуре от ползучести бетона.
3. Определяем, какой расчетный случай будет использован для проверки стального сечения.
σb,осн=17,35МПа<22МПа σr.осн=103,25 МПа<210 МПа где 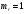 – коэффициент условий работы арматуры; – коэффициент условий работы арматуры; Rr = 210 МПа – расчетное сопротивление арматуры Материал плиты и балки работают упруго, следовательно согласно п. 9.19 СП 35.133330.2011 имеем расчетный случай А. 4. Произведемпроверку прочностипоясов металлического пролетного строения. Условие прочности в верхнем поясе(сжатие – плюс, растяжение – минус)  В этой формуле 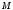 – полный изгибающий момент; – полный изгибающий момент;
Zbs=1,41 расстояние от центра тяжести стального сечения до центра тяжести бетонного сечения (плечо осевой силы 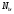 ). ).
Армирование плиты проезжей части принято двумя сетками с арматурой ø 10 мм класса A240. Количество продольных стержней на 1 пм – 13 штук в каждой сетке. Площадь арматуры в пределах расчетной ширины плиты 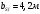 составит составит
Коэффициент условий работы верхнего стального пояса
Значение коэффициента 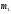 не может превышать величину, равную 1,2; принимаем не может превышать величину, равную 1,2; принимаем  Определим значение коэффициента ώ4. Максимальное значение поперечной силы в середине пролета моста
Среднее касательное напряжение в стенке балки: 
где tw = 0,017 м – толщина стенки балки; hw = 2,13 м – высота стенки балки Условие имеем 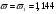 Далее определим коэффициент η При 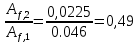 и 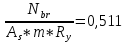 значение коэффициента  Здесь 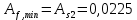 – площадь меньшего пояса стальной балки; – площадь меньшего пояса стальной балки; Aw=0,036 м2 - площадь стенки балки; 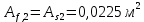 и и  –площади соответственно верхнего и нижнего поясов –площади соответственно верхнего и нижнего поясов Тогда поправочный коэффициент к моменту сопротивления при расчете прочности стальной балки на совместимое действие момента и продольной силы: 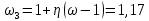 Поправочный коэффициент к моменту сопротивления при проверке стального верхнего пояса: 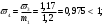 принимаем 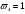  Условие выполняется. Прочность верхнего пояса обеспечивается Условие прочности в нижнем поясе 
57,41 МПа<416,4 МПа Значениекоэффициента η для нижнего пояса При 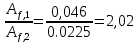 и 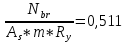 составит η = 0,84. Тогда 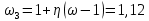
40,28 МПа<347 МПа Условие выполняется. Прочность нижнего пояса обеспечена. Расчет по касательным напряжениям Расчет производим в опорном сечении, т. е. в сечении с максимальной поперечной силой. Условие прочности 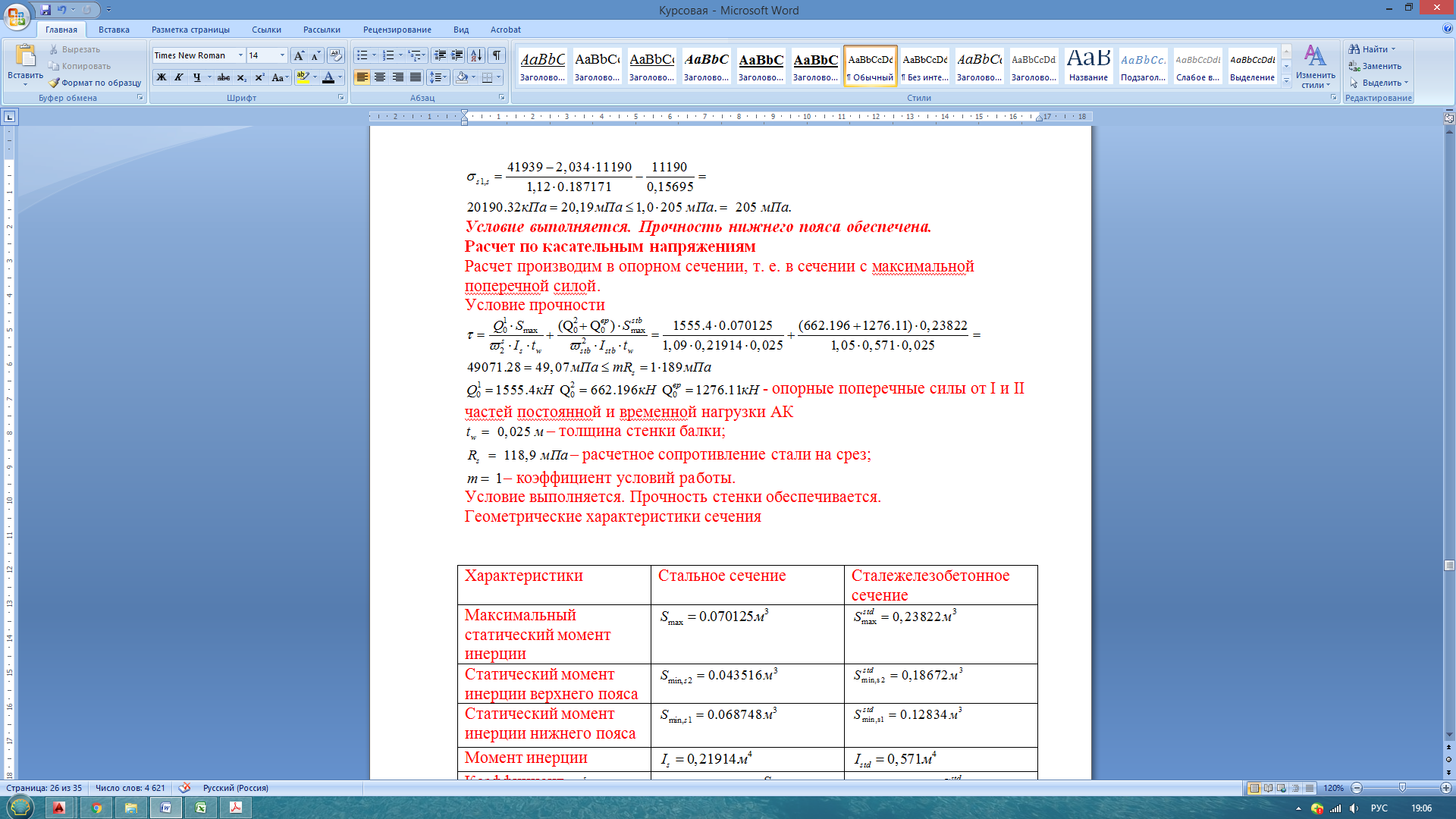
104,65 МПа<226,125 МПа Q0,1, Q0,2, Q0,вр- опорные поперечные силы от I и II частей постоянной и временной нагрузки АК tw – толщина стенки балки; Rs – расчетное сопротивление стали на срез; 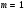 – коэффициент условий работы. – коэффициент условий работы.Условие выполняется. Прочность стенки обеспечивается. Геометрические характеристики сечения Расчет по главным (приведенным) напряжениям производим в четверти пролета Среднее касательное напряжение в стенке балки  где tw – толщина стенки балки; hw - высота стенки балки; Q= Q0,1+ Q0,2+Q0,вр - поперечная сила в четверти пролета.
105,74 МПа<201 МПа Условие выполняется. Второе из условий определяется зависимостью: 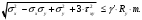 Определим значения напряжений, входящих в верхних волокнах стенки балки, где одновременно действуют достаточно высокие нормальные и касательные напряжения: а) нормальные продольные напряжения (σх)  М0,25,1, М0,25,2, М0,25,вр – изгибающие моменты в четверти пролета от I и II частей постоянной и временной нагрузок –расстояние от центра тяжести стального сечения до верхних волокон стенки балки Тогда
б) поперечные нормальные напряжения σу от местного действия постоянной и временной нагрузок определим по формуле 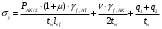
в) касательные напряжения τху в верхних волокнах стенки балки:  Q0,25,1, Q0,25,2, Q0,25,вр - значения поперечной силы в четверти пролета от первой и второй частей постоянной и временной нагрузок.
Тогда условие прочности примет вид: 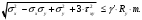 284,94 МПа<=381,7 МПа где γ' = 1,1 – коэффициент при σу ≠ 0. Условие прочности выполняется. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
