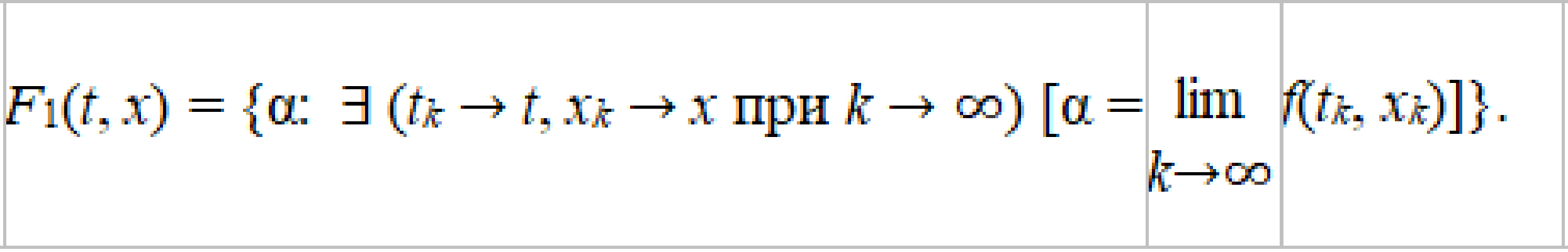Теорема Каратеодори. Курсовая работа (1). Курсовая работа Теорема Каратеодори
 Скачать 2.78 Mb. Скачать 2.78 Mb.
|
|
Курсовая работа Теорема Каратеодори
Содержание Введение…………………………………………………………………………3 1. Обоснование необходимости обобщения понятия решения дифференциального уравнения…………………………………………..5 2. Теорема Каратеодори…………………………………………………………7 3. Определения решения………………………………………………………..15 4. Заключение……………………………………………………………………19 5. Список литературы…………………………………………………………...20 Введение Актуальность данной темы в значительной степени обусловлена многочисленными приложениями теории дифференциальных уравнений с разрывными правыми частями. Ряд процессов в механике, электротехнике и в других областях характеризуются тем, что правые части дифференциальных уравнений, которые описывают их динамику, претерпевают разрывы в зависимости от текущего состояния процесса. Стандартный пример такой динамической системы – механическая система с сухим трением, когда сила сопротивления может принимать одно из двух противоположных по знаку значений в зависимости от направления движения. Рассмотрим эту систему подробнее. Механическая система с сухим трением. Можно установить зависимость между работой, затраченной на преодоление сил трения и скоростью движения. Эта зависимость получается совершенно различной для случая движения груза массы m в жидкости и трения о какую-либо твердую поверхность. В первом случае (случай “жидкого трения”) работа существенно зависит от скорости и при уменьшении скорости уменьшается и может быть сделана как угодно малой. Во втором случае (случай “сухого трения”), наоборот, работа мало зависит от скорости, и как бы медленно ни двигали груз, необходимо затратить на его перемещение некоторую конечную и вполне определенную работу, т.е. сила трения даже при сколь угодно малой скорости имеет конечную величину. Кроме этого, учитывая, что сила трения всегда направлена в сторону, противоположную скорости, и, значит при переходе через нуль сила трения меняет знак на обратный, в случае “жидкого трения” получаем, что сила трения без скачка проходит через нуль и меняет при этом знак: В случае же “сухого трения” при скорости, стремящейся к нулю, сила трения с двух сторон стремится к разным конечным пределам (в частности противоположным по знаку, но одинаковым по абсолютной величине), т.е. при нуле претерпевает разрыв: Т.о. математические модели механических систем с кулоновым трением, полученные в рамках механики систем абсолютно твердых тел, представляют собой дифференциальные уравнения, правые части которых являются функциями, разрывными относительно обобщенных скоростей (сила трения изменяется скачкообразно при изменении направления движения). 1. Обоснование необходимости обобщения понятия решения дифференциального уравнения Решением дифференциального уравнения x = f(t,x) (1)  Для дифференциальных уравнений с разрывными правыми частями такое определение непригодно, как показывают следующие примеры. Пример 1.            Пусть правая часть дифференциального уравнения (1) непрерывно зависит от x и может быть разрывной только по t. Тот факт, что в случае непрерывной функции f задача Коши для уравнения (1), порожденная начальным условием
эквивалентна интегральному уравнению
наводит на мысль назвать решением задачи (1) – (2) решение уравнения (3) и в ситуации, когда f разрывна. Один из наиболее известных и распространенных наборов условий на правую часть уравнения (1), при которых такой подход к расширению понятия решения оказывается содержательным в математическом плане и полезным и адекватным в приложениях выглядит следующим образом. Предполагается, что: 1) функция x → f(t, x) непрерывна почти при всех t; 2) функция t → f(t, x) измерима при каждом x; 3) существует локально суммируемая функция m: R → R такая, что при каждом фиксированном x почти при всех t выполняется неравенство ||f(t, x)|| ≤ m(t). Эти условия носят название условий Каратеодори. Они, в частности, гарантируют, что если функция t → x(t) измерима, то функция t → f[t, x(t)] измерима и локально суммируема. Отсюда следует теорема. 2. Теорема Каратеодори Теорема 1. Каратеодори. Пусть функция f: R → Rn удовлетворяет условиям Каратеодори. Тогда задача (1) – (2) на любом промежутке [t0 – T, t0 + T] имеет по крайней мере одно решение Каратеодори. Доказательство. Для произвольного натурального k определим на [t0 – T, t0 + T] функцию xk с помощью равенства
и рекуррентного (по i) соотношения
(i = 1, ..., [T/k] + 1; здесь [a] — целая часть числа a). В силу условий Каратеодори, как отмечалось выше, подынтегральная функция в (6) измерима и суммируема, так что интеграл в правой части соотношения (6) имеет смысл Далее, если положить
то, во-первых,  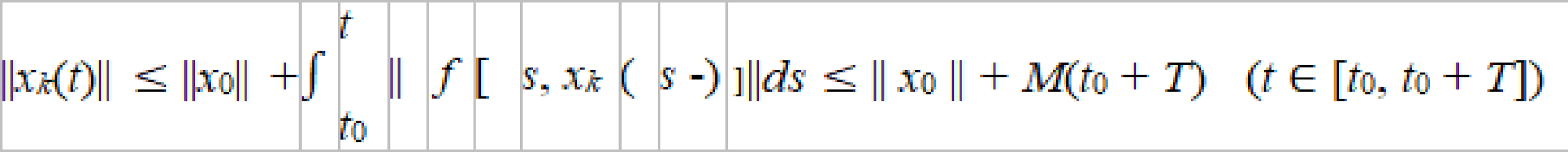 (5) (5)и, во-вторых,
Пример 2. = 1 - 2signx     x 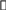       Кроме этого, уравнение с непрерывной правой частью равносильно интегральному уравнению  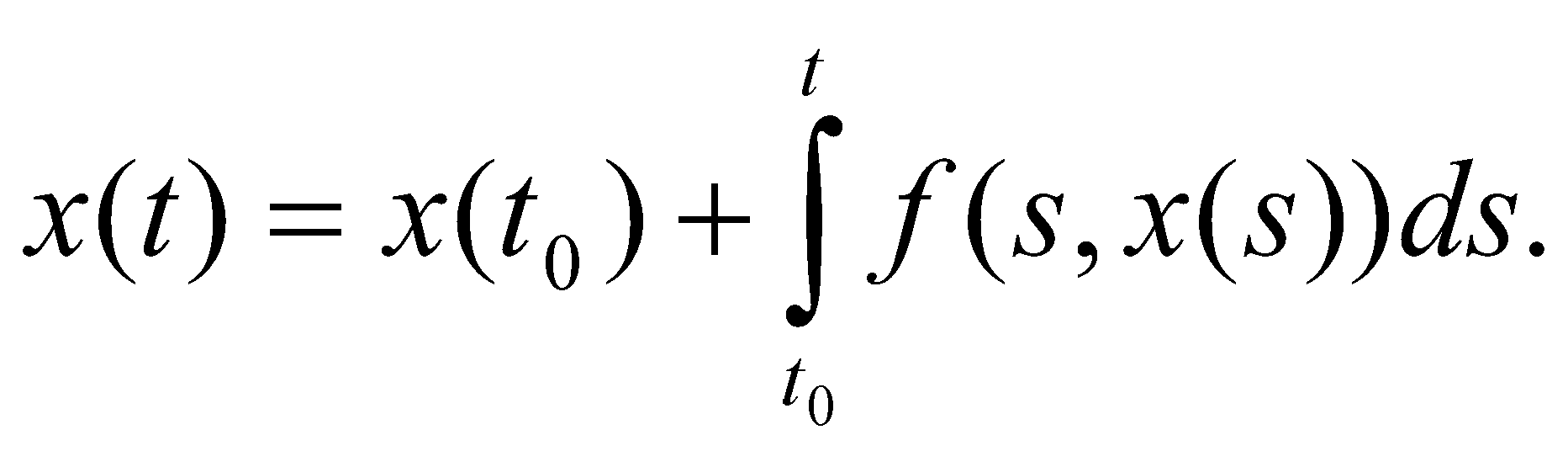 В случае, когда f(t,x) разрывна по t и непрерывна по x, решением уравнения можно назвать функции, удовлетворяющие интегральному уравнению. В этом случае, решения с одной стороны от S подходят к S, а с другой стороны сходят с S (траектории “прошивают” поверхность): S    В другом случае, когда с обеих сторон поверхности разрыва S решения приближаются к S (траектории “стыкуются” – скользящий режим), это определение решения непригодно, т.к. ничего не говорит о том, как продолжится решение, попавшее на S . Необходимо поэтому было дать такое определение решения, которое охватило бы эти два основных случая и формулировалось бы независимо от расположения линий и поверхностей разрыва. Рассмотрим обыкновенное дифференциальное уравнение. y’ = f(x,,...,), s = (7)  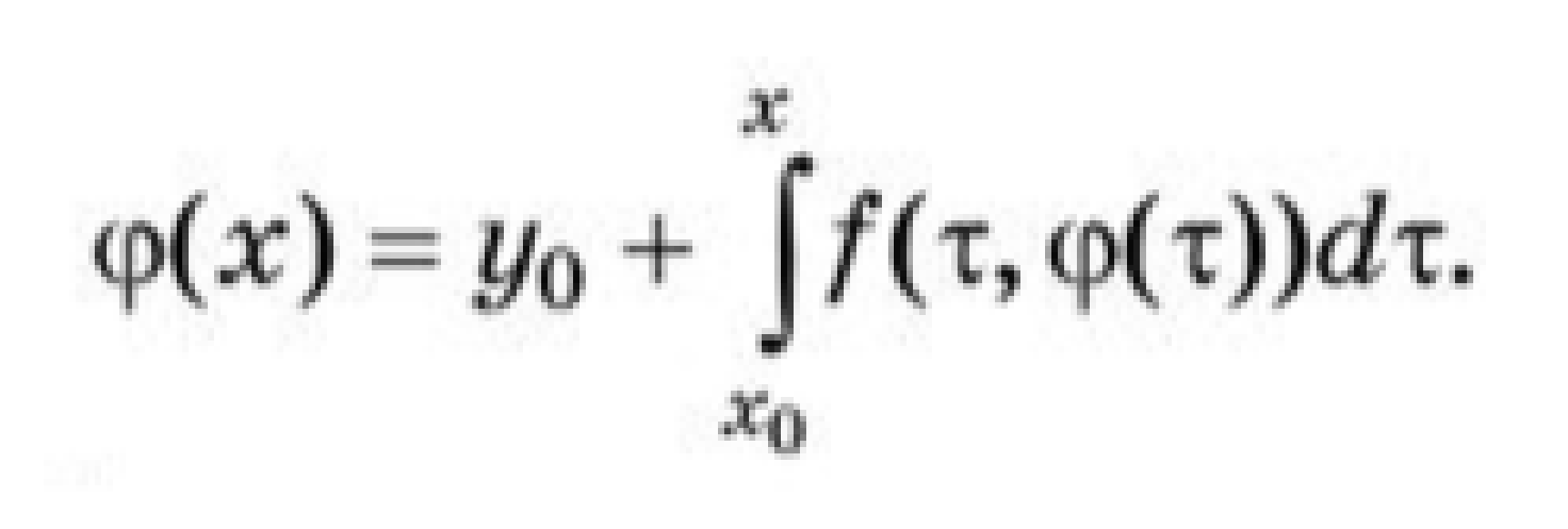 (8) Интеграл в (8) существует для многих не непрерывных функций. Непрерывность функции гарантирует принадлежность решения (7) к классу непрерывно дифференцируемых функций. Таким образом, если не требовать непрерывной дифференцируемости решений (7), то можно будет не ограничиваться непрерывными функциями f.  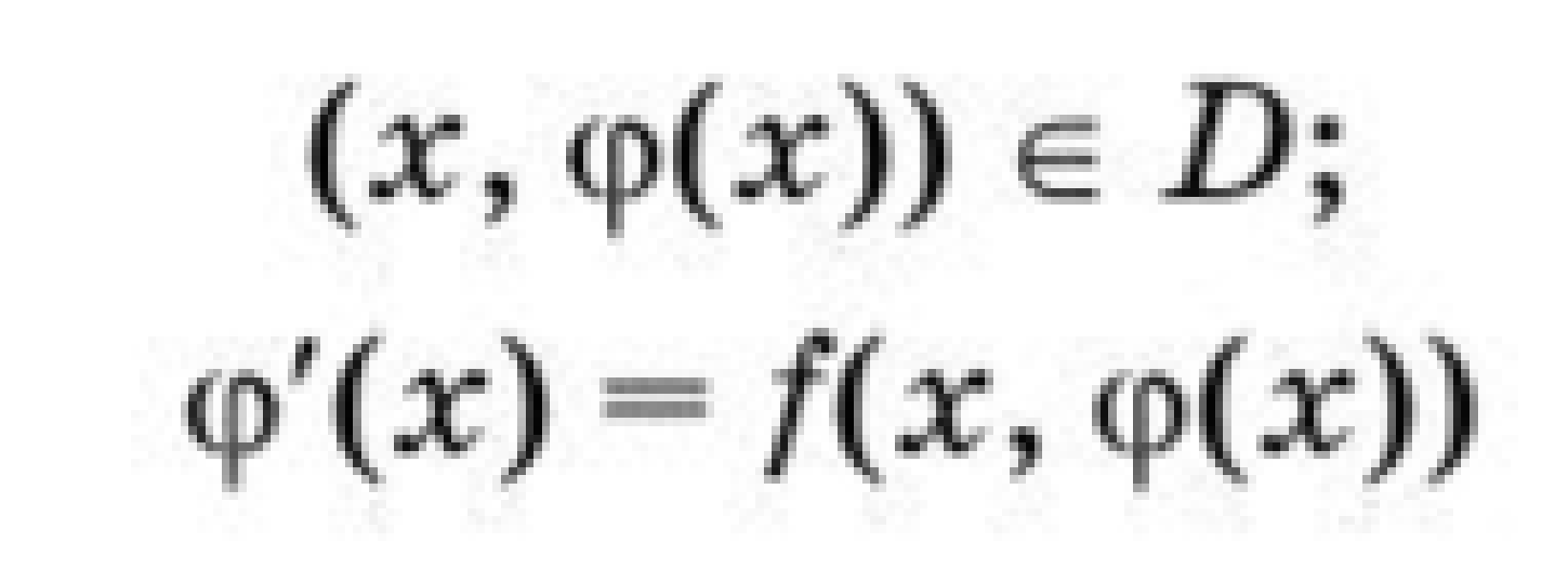 (9) (10) для всех х ∊ (α; ß), исключая множество лебеговой меры нуль. Если такие интервал (α; ß) и функция φ существуют, то φ называется решением системы (7) на (α; ß) в расширенном смысле. Заметим, что абсолютная непрерывность решения гарантирует существование производной φ' почти всюду на (α; ß) (т. е. исключая множество лебеговой меры нуль), так что условие (10) имеет смысл почти всюду. Если f ∊ C(D) и φ — решение системы (26) в предыдущем смысле, то из тождества(29) следует, что φ' ∊ C(D) на (α; ß), и, следовательно, более общее понятие уравнения (26) и решения ф сводится к обычному определению (26), когда f ∊ C(D). Относительно существования решения системы (26) Каратеодори доказал следующую теорему в предположении, что f ограничена интегрируемой по Лебегу функцией от х. Доказательство приводится только для случая п = 1 (для случая п > 1 доказательство проводится аналогично). Обозначим R: |x - | ≤ a, |y - | ≤ b, где (, ) — фиксированная точка, а а и b — положительные действительные числа. Теорема 2 (Теорема Каратеодори существования). Пусть функция f определена на R, измерима по х при каждом фиксированном у и непрерывна по у при каждом фиксированном х. Если на интервале |х - |≤ а существует интегрируемая по Лебегу функция т, такая,что  то на некотором интервале |x - | ≤ h(h > 0) существует решение φ в расширенном смысле, удовлетворяющее условию φ() = Доказательство. Рассмотрим случай х≥(в случае х≤ ситуация аналогична). Определим функцию М следующим образом:  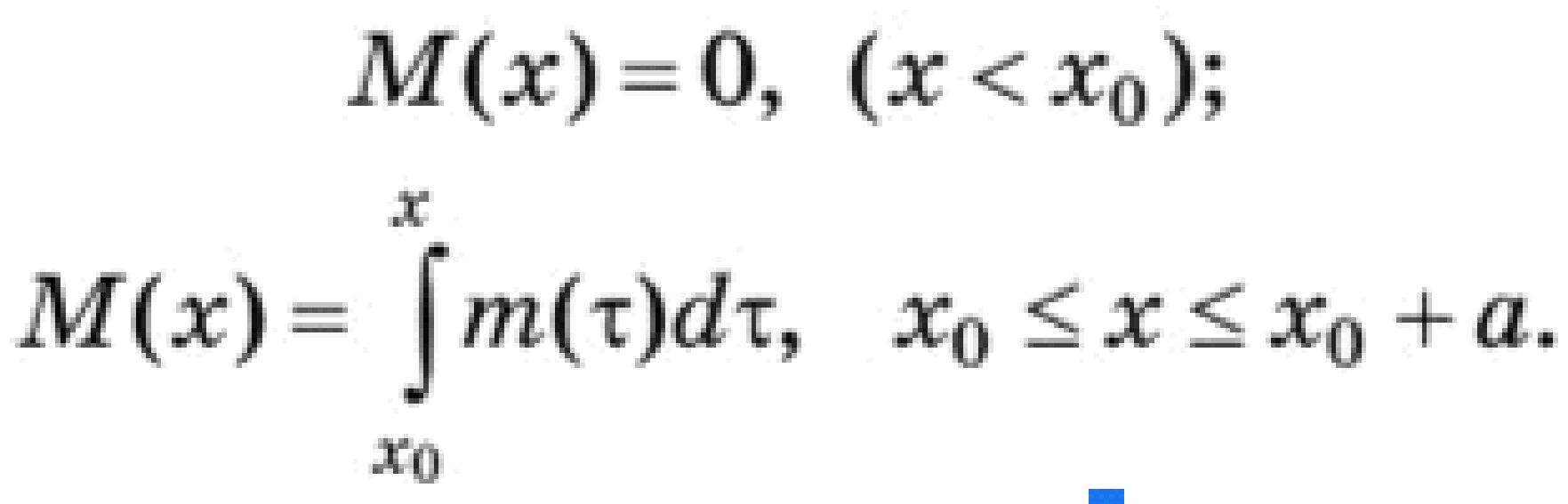 (12) (12) 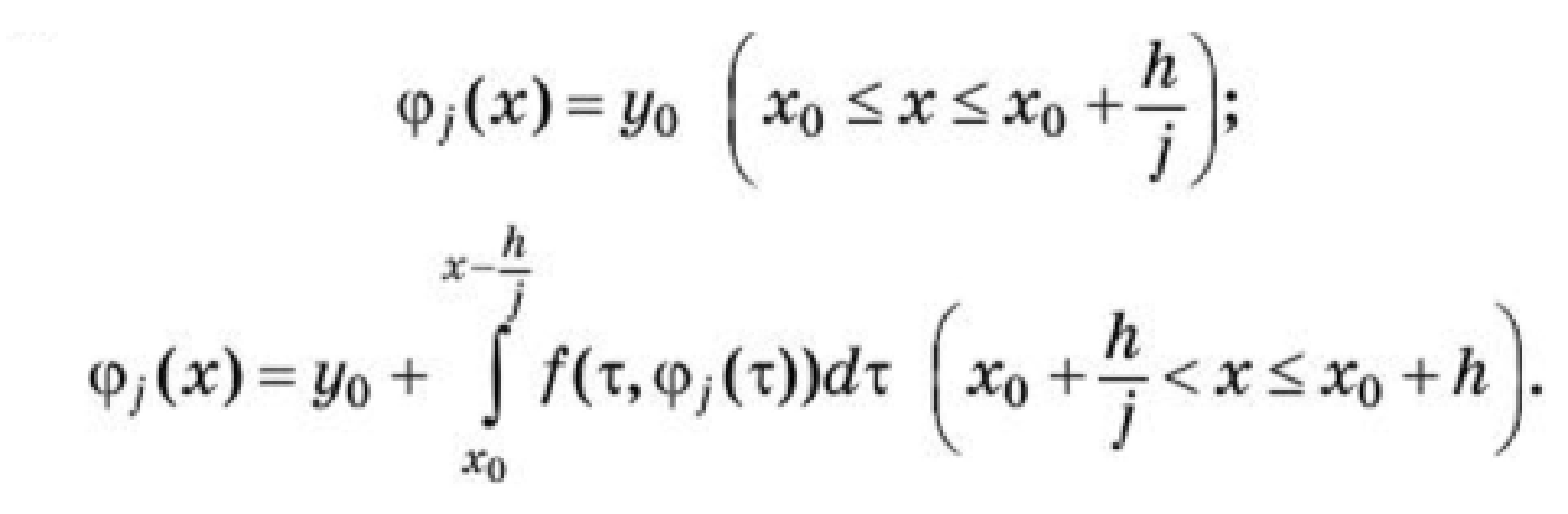 (13) (14)  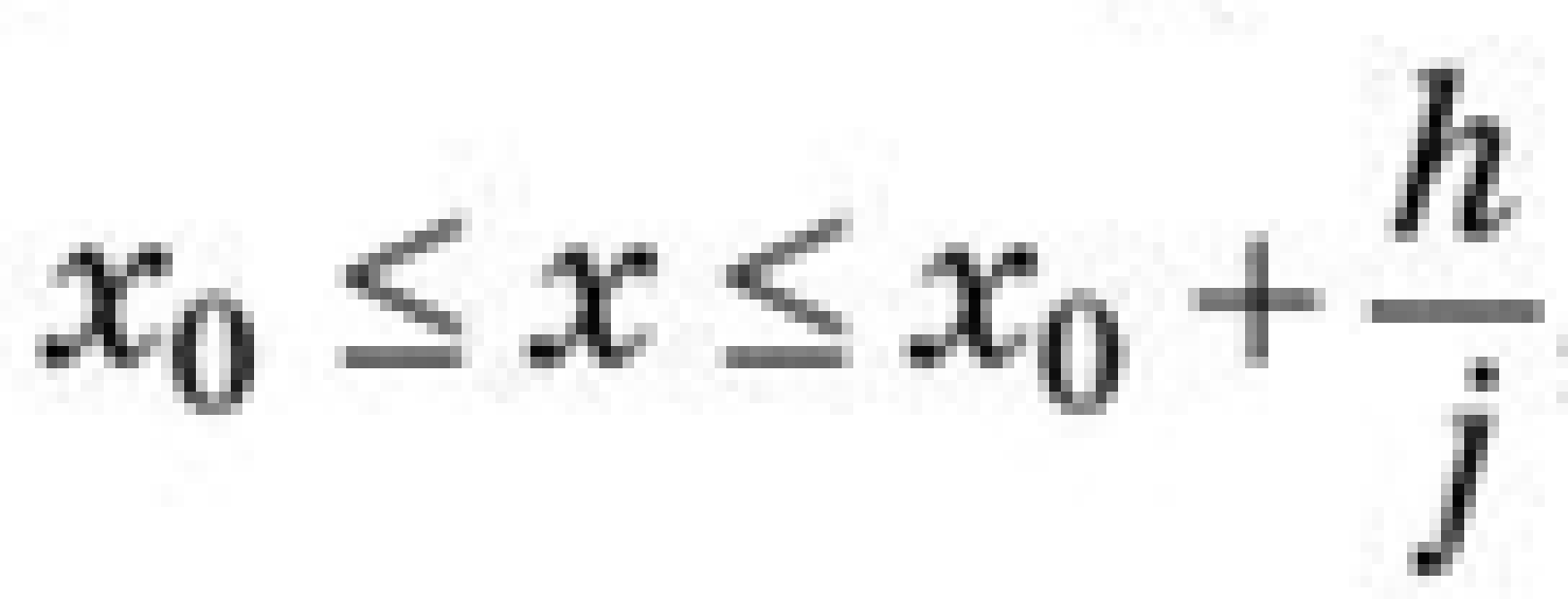     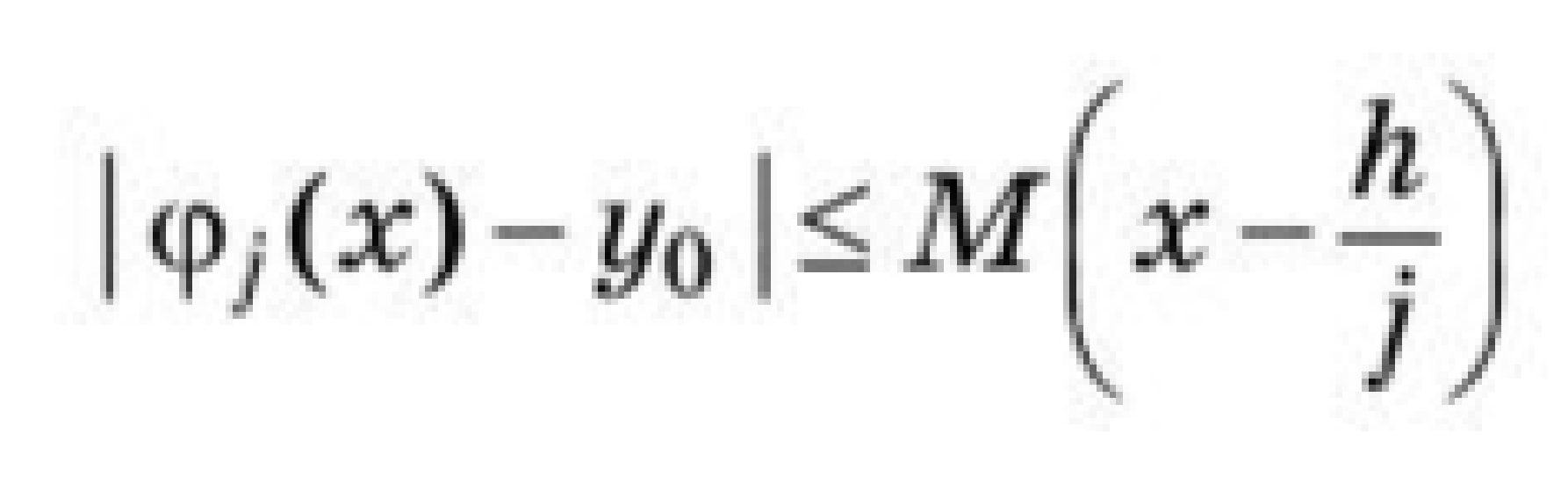 (15) в силу (11) и (12). Предположим, что определена для причем 1 < k < j. Тогда формула (14) определяет для + < x ≤+ ,  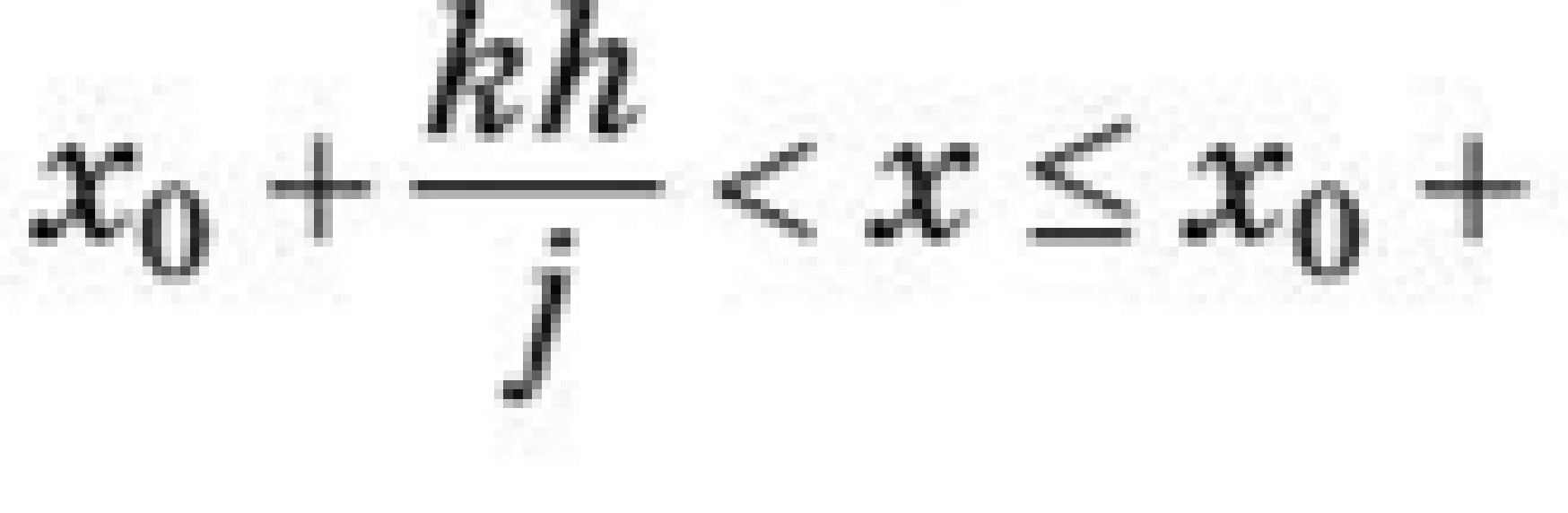  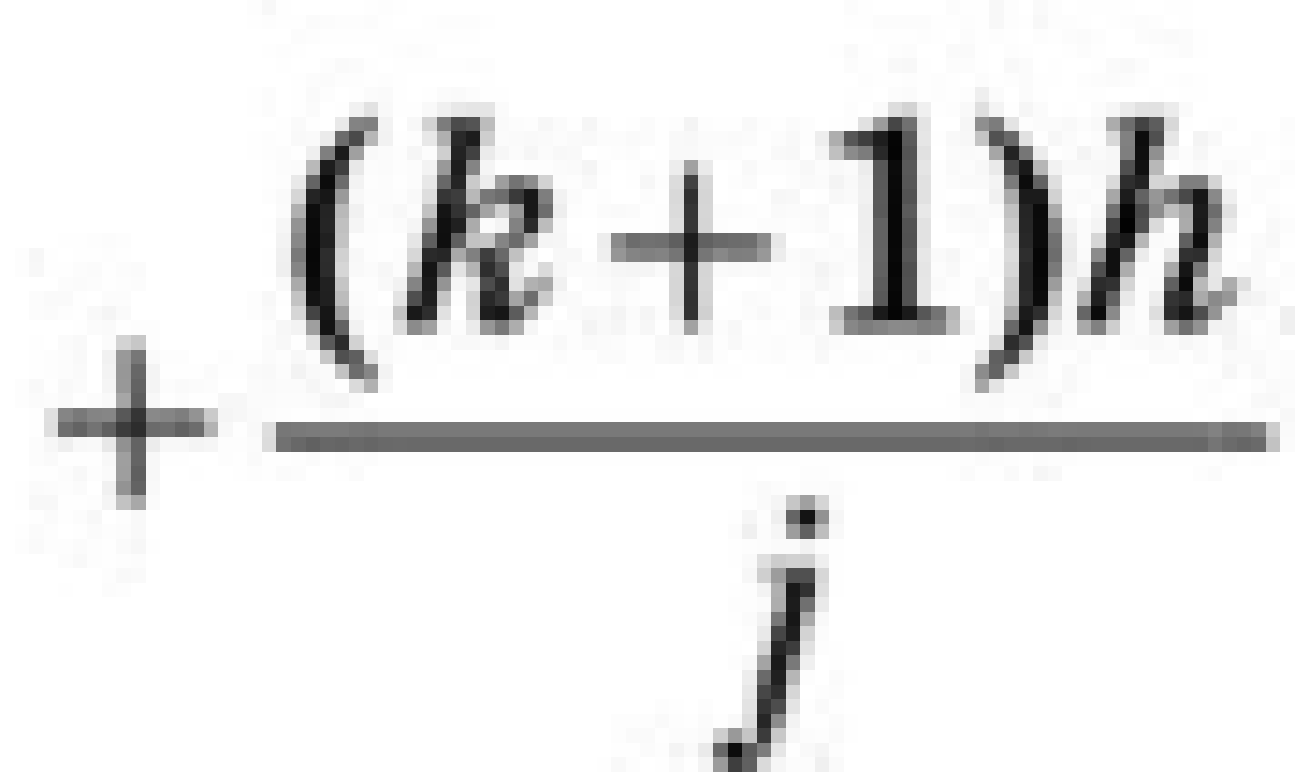 неравенству (15) в силу (11) и (12). Поэтому, по индукции, формулы (13)-(14) определяют все фу как непрерывные функции на интервале ≤х≤+ h удовлетворяющие условиям  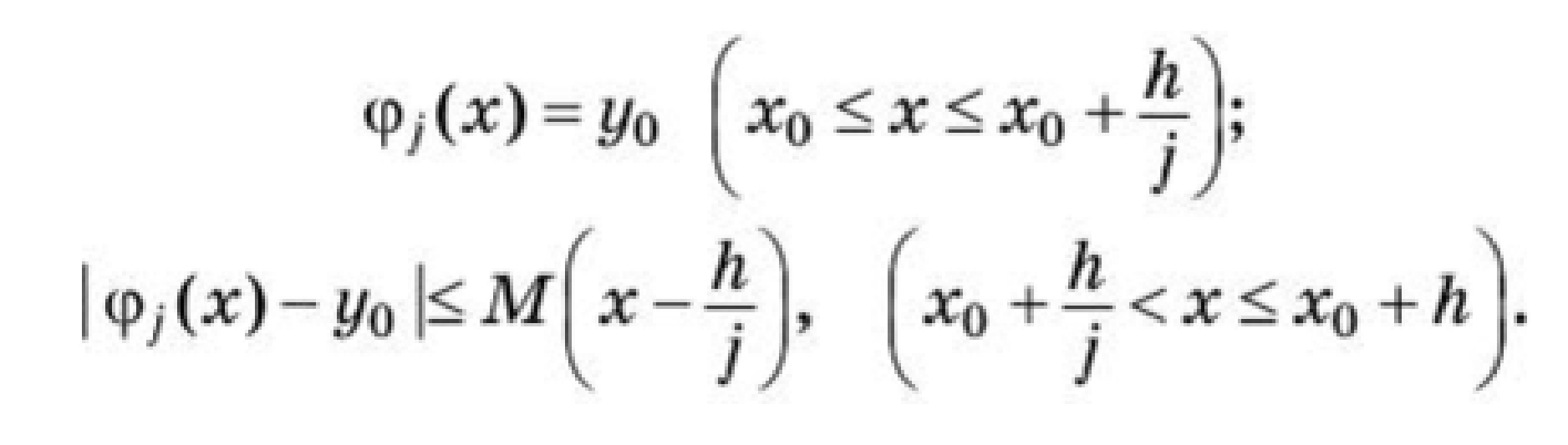 (16) (16)Если и — любые две точки интервала [; + h], то в силу (11)-(14)  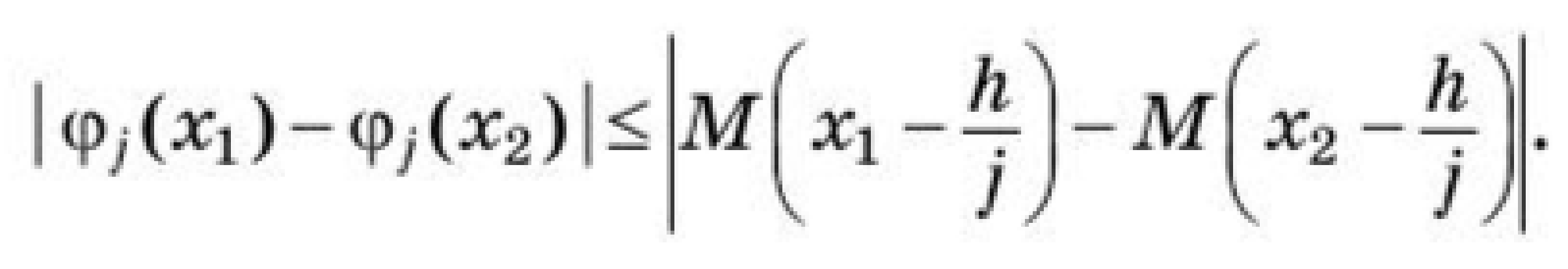 (17) (17)Так как функция М непрерывна на интервале [; + h], то она на этом интервале равномерно непрерывна. Поэтому из (17) следует, что множество {} на интервале [; + h] равностепенно непрерывно. Далее, из (16) следует, что множество {} на [; + h] ограничено. Поэтому из теоремы Арцела о том, что если множество функций, определенных на конечном интервале, равномерно ограниченное, равностепенно непрерывное, то оно содержит равномерно сходящуюся последовательность, получаем, что существует подпоследовательность {}, которая сходится при k —> ∞ равномерно на [; + h] к непрерывному пределу . Из (8) следует неравенство  и так как f при фиксированном х по у непрерывна, то  для каждого фиксированного x из интервала [; + h]. Поэтому из теоремы Лебега об интегрировании мажорируемых последовательностей следует, что  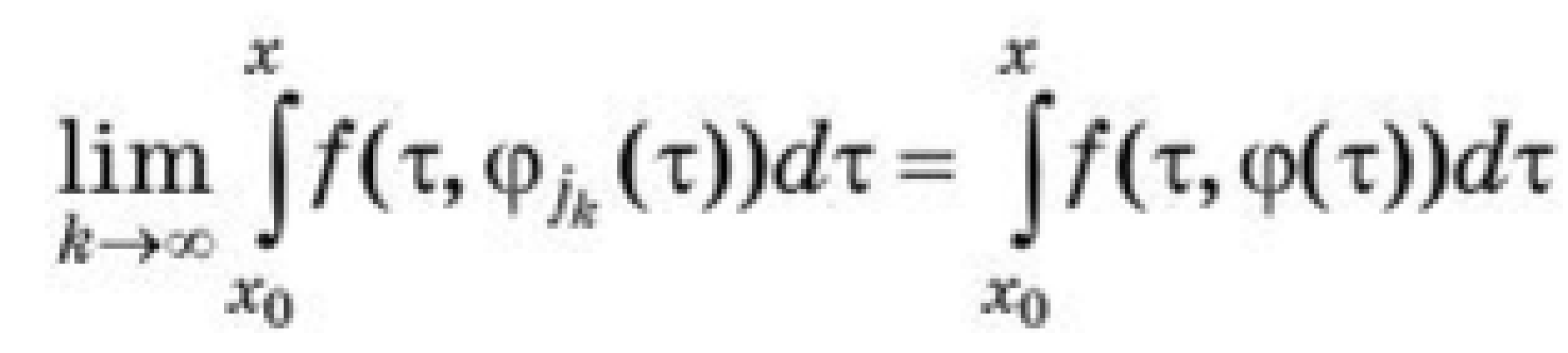 (18) (18) 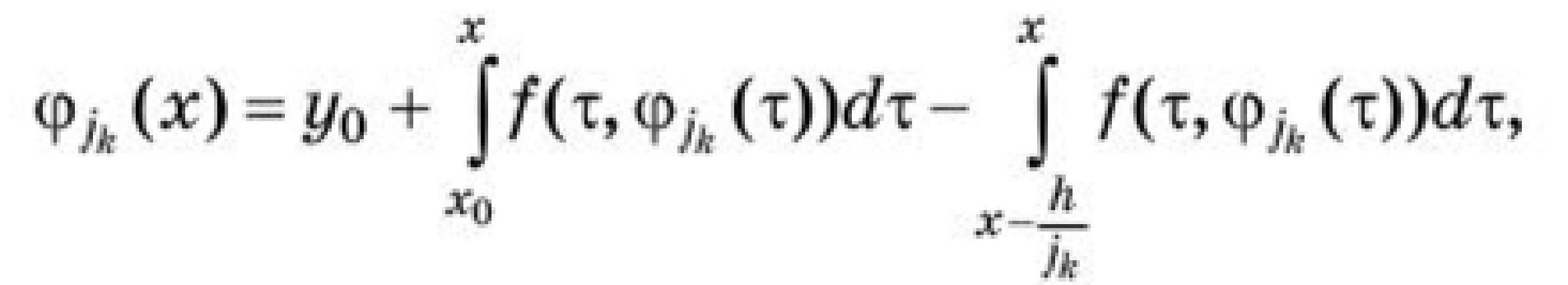 Но причем очевидно, что последний интеграл при k → ∞ стремится к нулю.  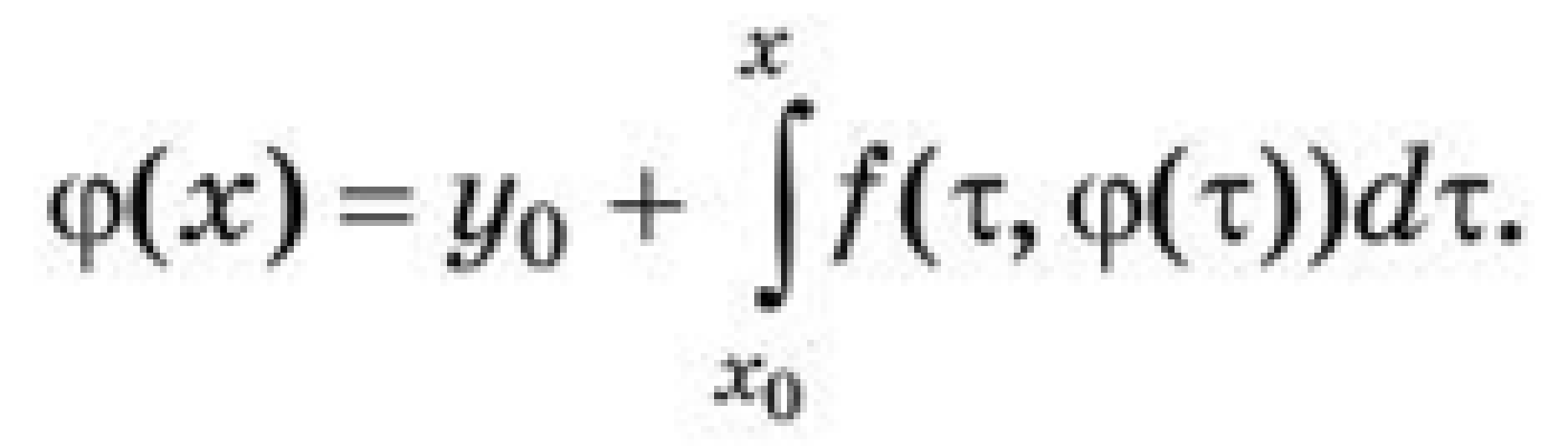 Теорема доказана. Теорема доказана. 3. Определения решения Рассмотрим уравнение или систему в векторной записи x = f(t,x), (1)       Определение 1.Решением уравнения (1) называется решение дифференциального включения x ∊ F(t,x), (2) т.е. абсолютно непрерывная вектор-функция x(t), определенная на интервале или отрезке I, для которого почти всюду на I x ∊ F(t,x(t)). Другими словами, решение дифференциального уравнения (1) определяется как функция, у которой производная x =        Пример 3. Рассмотрим решение дифференциального включения
Решением дифференциального включения (1) на отрезке [a, b] называют абсолютно непрерывную функцию φ: [a, b] → R, для которой почти всюду на [a, b]производная φ′(t) принадлежит множеству F[t, φ(t)]. В такой ситуации решением дифференциального уравнения x=f(t,x) с разрывной правой частью называют решение дифференциального включения (1). Одна из возможных процедур построения многозначного отображения f состоит в следующем. Для любых (t, x) ∊ R×R обозначим через F1(t, x) множество предельных значений функции f в точке (t, x):
Многозначное отображение F определим равенством
здесь co F1(t, x) обозначает выпуклую замкнутую оболочку множестваF1(t, x), т. е. минимальное выпуклое замкнутое множество, содержащее F1(t, x) — в нашем случае вещественнозначной функции f, очевидно, co F1(t, x) представляет собой отрезок. Очевидно также, что F(t, x) состоит из одной точки f(t, x), если функция f в точке (t, x) непрерывна. Пример 4. Решить систему  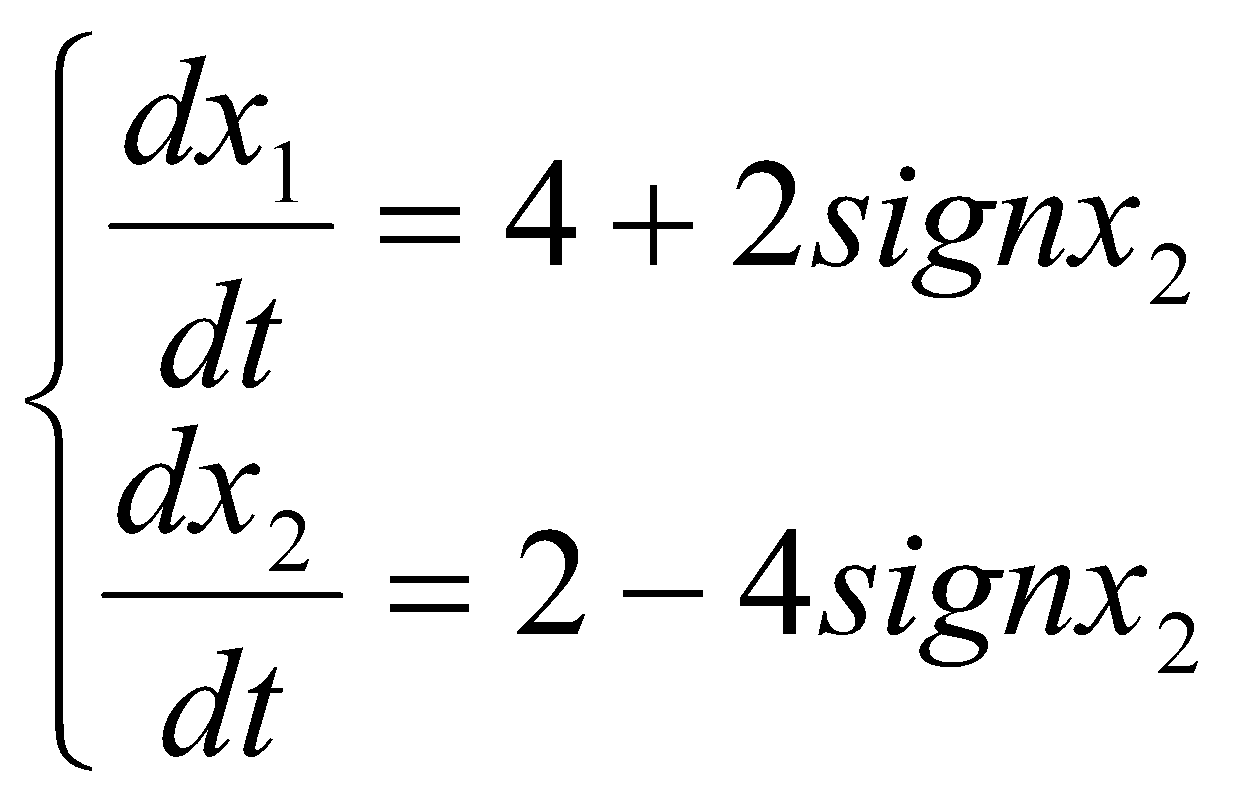        Отложим из точки М эти два вектора и соединим их концы отрезком АВ:              Заключение В данной работе излагаются основные направления теории дифференциальных уравнений с разрывной правой частью и указываются ее применения для описания механических систем. Исследуются основные свойства таких уравнений. Исследуются особенности, возникающие на линиях или поверхностях разрыва правой части уравнения и на их пересечениях. Большое число задач из механики, электротехники и теории автоматического управления, описываемых этими уравнениями. Показывается, что многие утверждения классической теории дифференциальных уравнений остаются справедливыми и для уравнений с разрывными правыми частями СПИСОК ЛИТЕРАТУРЫ Филиппов А.Ф. Устойчивость для диф. уравн. с разрывными и многозначными правыми частями. – Диф. уравн., 1979, 15, № 6, 1018-1027. Филиппов А.Ф. Дифференциальные уравнения с разрывной правой частью. – Математический сборник, 1960, 51, № 1, 99-128. Филиппов А.Ф. дифференциальные уравнения с разрывной правой частью. – М.: Наука, 1985. Филиппов А.Ф. Система диф. уравн. с несколькими разрывными функциями. – Математические заметки, 1980, 27, № 2, 255-266. Матросов В.М. О дифференциальных уравнениях и неравенствах с разрывными правыми частями I, II. – Диф. уравн.,1967, 3, № 3, 395-409; № 5, 869-878. Айзерман М. А., Пятницкий Е. С. Основы теории разрывных систем I, II. – Автоматика и телемеханика, 1974, № 7, 33-47, № 8, 39-61. Берман Г. Н. Сборник задач по курсу математического анализа 22-е изд. 2001. Берман Г. Н. Сборник задач по курсу математического анализа 20-е изд. 1985. Бугров Я.С. Никольский С.М. Высшая математика/ Под ред.Садовничего В.А.-Дрофа 2005. Ильин В.А. Высшая математика. Учебник. - М.: Проспект,2002. |


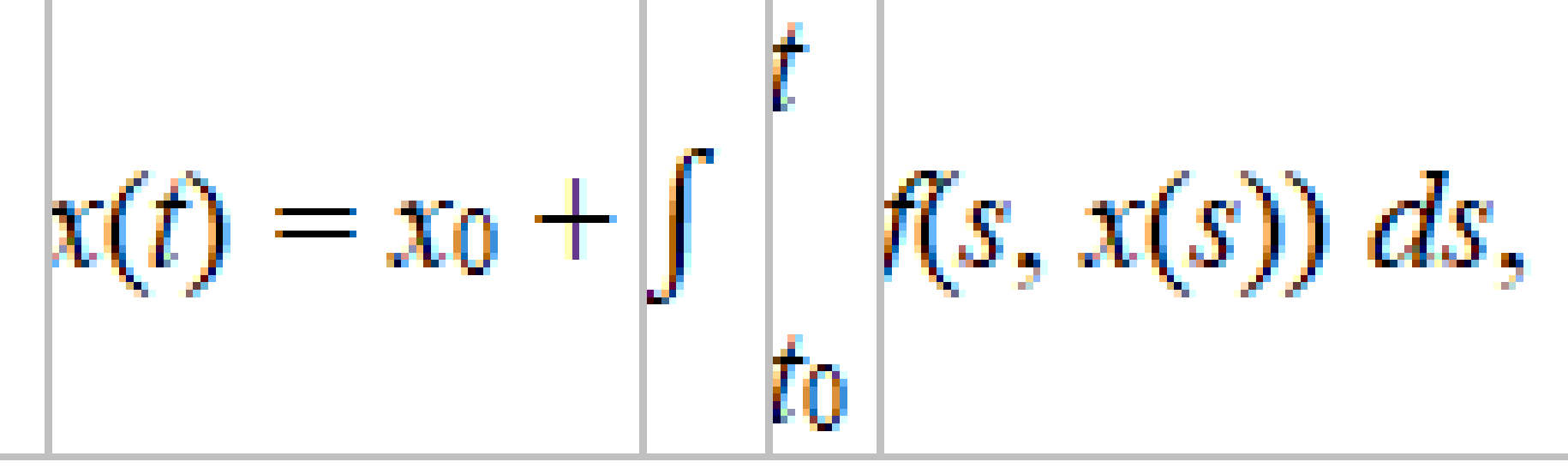



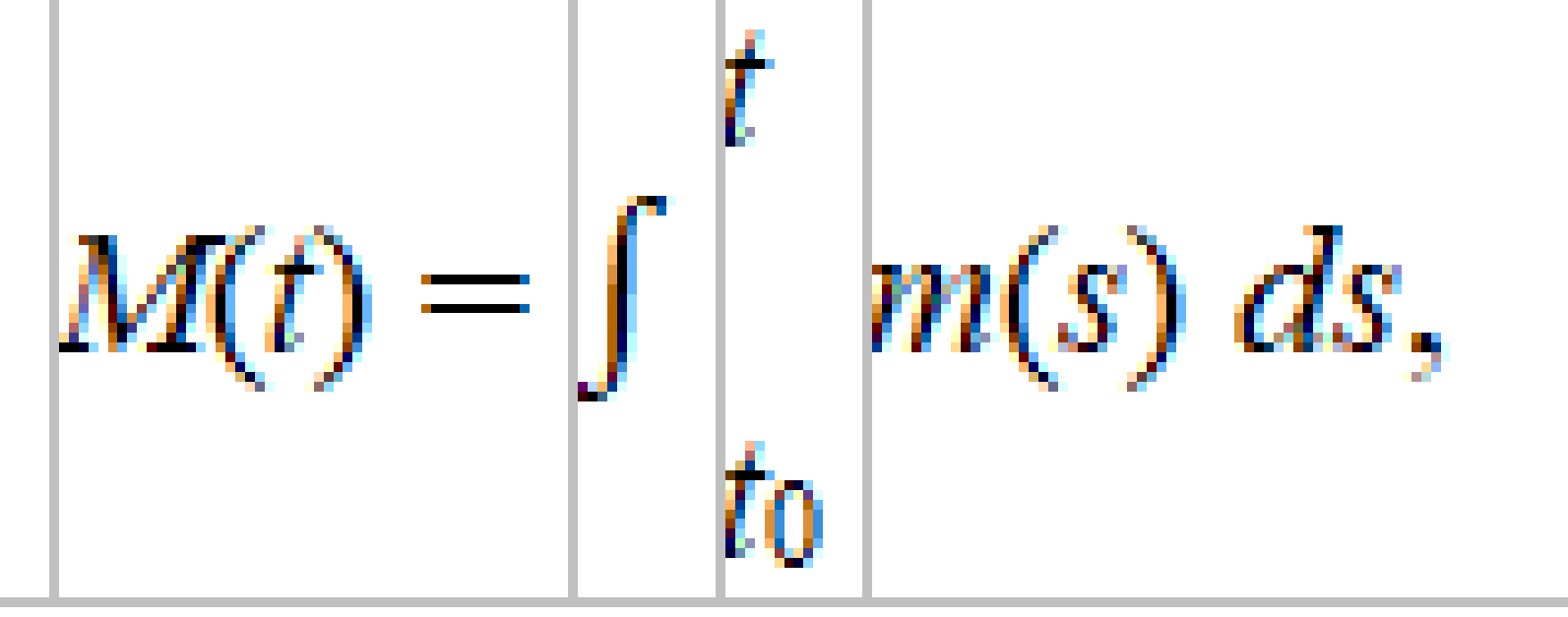

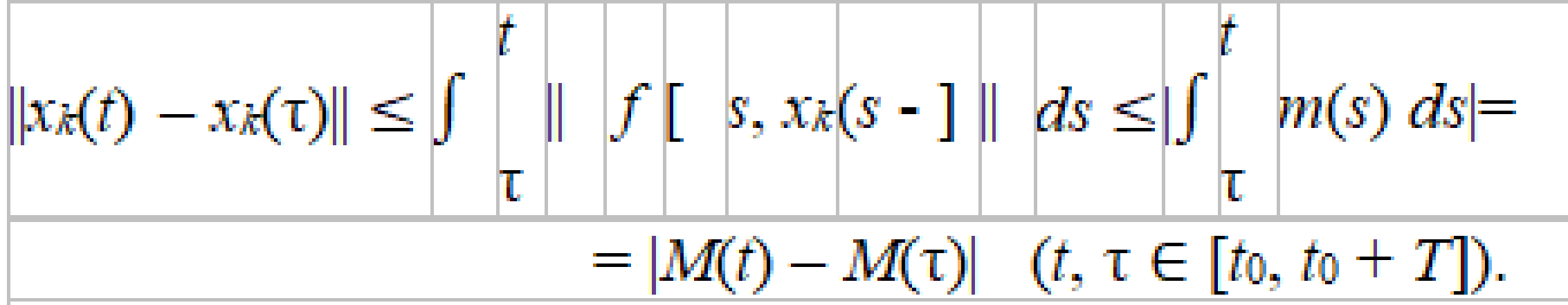 (6)
(6)