|
|
ОТС курсовик 56. Курсовая работа учебная дисциплина Общая теория связи
-
                                                                                                                                                                                     Федеральное государственное образовательное бюджетное Федеральное государственное образовательное бюджетное
учреждение высшего профессионального образования
«Санкт-Петербургский государственный университет
телекоммуникаций им. проф. М. А. Бонч-Бруевича»
__________________________________________________________
Факультет многоканальных телекоммуникационных систем
Кафедра
теоретических основ связи и радиотехники
КУРСОВАЯ РАБОТА
учебная дисциплина «Общая теория связи»
Тема:«Расчёт основных характеристик цифровой системы связи
с использованием квадратурной модуляции»
Выполнила студенткаII курса группы
ИКТ-113Мизгунова А. С.
номер зачётной книжки 112056;
номер выполненного варианта  =56 =56
Проверил руководитель
Оценка __________(подпись)
Санкт-Петербург - 2013
|
Цель курсовой работы – изучить принципы работы системы цифровой передачи аналоговых сообщений и рассчитать основные характеристики входящих в нее функциональных узлов.
1. Структурная схема системы цифровой связи
Система связи предназначена для передачи аналоговых сообщений по цифровому каналу связи. Структурная схема дляКАМ-16 и КФМ-4 представлена на рис. 1.1.
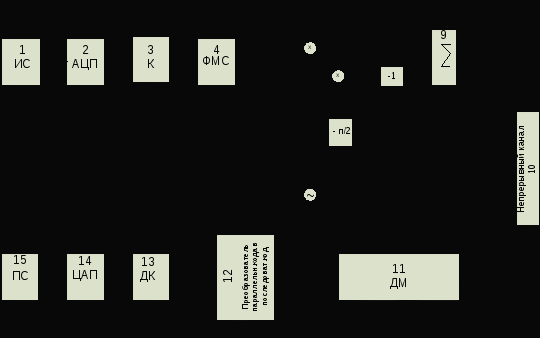
Рис. 1.1. Структурная схема системы цифровой связи.
Входящие в систему цифровой связи функциональные узлы имеют следующие назначения:
источник сообщений создает реализацииa(t) случайного процесса A(t);
аналого-цифровой преобразователь преобразует аналоговый сигнал от источника сообщения в последовательность его двоичных цифровых отсчетов;
кодер включает в цифровой поток от АЦП дополнительные символы, предназначенные для повышения помехоустойчивости системы связи;
формирователь модулирующих сигналов служитдля получения модулирующих сигналовI(t) и Q(t), соответствующих заданному виду модуляции;
перемножители – для получения БМсигналов:синфазного I(t)cosωСtи квадратурногоQ(t)sinωСt.
фазовращатель–для получения второго несущего колебания, ортогонального по отношению к первому;
генератор гармонических колебаний – для получения несущего колебания;
сумматор для объединения синфазного и квадратурного сигналов в единый сигнал с квадратурной модуляцией SКАМ(t) = I(t)cosωСt + Q(t)sinωСt;
непрерывный канал – среда распространения сигнала SКАМ(t);
демодулятор – для анализа приходящего сигнала, искаженного помехами, и принятии решения о переданном сообщении;
преобразователь параллельного кода в последовательный код – для преобразования сигнала с выхода демодулятора в последовательный формат кодовых комбинаций;
декодер – для исправления части ошибок, возникших при приёме сообщений вследствие влияния помех;
цифро-аналоговый преобразователь – для восстановления аналоговой формы сигнала по принятым его цифровым отсчетам;
получатель сообщений.
2. ИСХОДНЫЕ ДАННЫЕ
Номер выполняемого варианта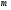 определяется двумя последними цифрами в номере зачетной книжки (98) Используя номер варианта определяется двумя последними цифрами в номере зачетной книжки (98) Используя номер варианта 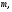 внести свои данные в табл. 1. внести свои данные в табл. 1.
Таблица 1
Предельные уровни
аналогового сигнала
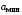 , , 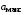 (В) (В)
|
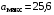 (В) (В)
|
Внести
свои данные
|
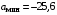 (В) (В)
|
Верхняя частота спектра
аналогового сигнала 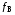
|
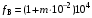 (Гц) (Гц)
|
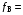 1,56 ∙10 4 (Гц) 1,56 ∙10 4 (Гц)
|
Заданный уровень
квантования
|
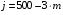
|
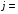 332 332
|
Спектральная плотность
мощности
флуктуационной
помехи
|
Номер варианта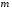
в пределах
|
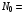 2,3∙10-7 2,3∙10-7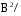 Гц Гц
|
1…33
|
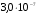
|
34…66
|
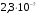
|
67…99
|
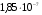
|
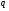 – номер тактового – номер тактового
интервала ошибки
|
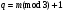
|
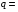 3 3
|
№ вида модуляции
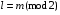
|
Вид модуляции
|
Вид модуляции
почислу 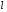
|
0
|
КФМ-4
|
+
|
1
|
КАМ-16
|
|
КАМ-16 (QAM) квадратурная амплитудная модуляция
КФМ-4 (QPSK) квадратурная фазовая модуляция
NO (В2/Гц) – спектральная плотность мощности флуктуационной помехи
J10=500-3m – заданный уровень квантования
fB = (1+m)·104 (Гц) – Верхняя частота спектра аналогового сигнала
q = mmod 3 + 1 – номер тактового интервала ошибки
3. Расчет системы цифровой связи
3.1. Источник сообщения
Источник сообщения (ИС) вырабатывает реализации 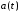 стационарного случайного процесса стационарного случайного процесса 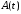 типа квазибелого шума с параметрами типа квазибелого шума с параметрами 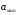 , ,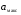 и и 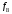 . Мгновенные значения сообщения равновероятны в интервале от значения . Мгновенные значения сообщения равновероятны в интервале от значения 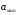 до значения до значения 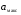 . .
Требуется:
Написать аналитические выражения для плотности вероятности w(a) мгновенных значений сообщения, функции распределения 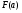 и построить их графики. и построить их графики.
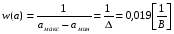
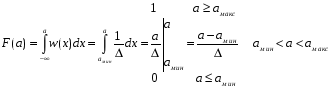
где 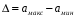 = 51,2 В. = 51,2 В.
Графики 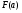 иw(a) приведены на рис. 3.1.1. иw(a) приведены на рис. 3.1.1.
F(a)
1
-25,6 0 25,6a(В)
w(a) (1/В)
-25,6 0 25,6a(В)
Рис. 3.1.1. Графики функции распределения и плотности вероятности 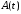
Рассчитать математическое ожидание M[A(t)] и дисперсию D[A(t)]
сообщения A(t).
2
2
2
1
)
(
)
(
2
2
2
мин
макс
минí
макс
минí
макс
a
a
минí
макс
a
a
a
a
a
a
a
da
a
a
a
da
a
aw
t
A
M
макс
мин
M[A(t)] = 0
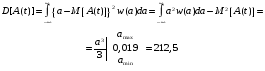
Написать аналитическое выражение для спектральной плотности мощности 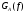 сообщения сообщения 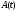 и построить график. и построить график.
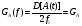 = 212,5/(2∙1,56∙104)= 6,8мВ2/Гц = 212,5/(2∙1,56∙104)= 6,8мВ2/Гц
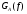 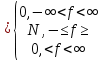
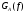
- fв fв
Найти аналитическое выражение для корреляционной функции 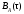 сообщения сообщения 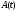 и построить график. По форме графика и построить график. По форме графика 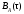 определить, является ли сообщение определить, является ли сообщение 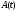 эргодическим случайным процессом или не является таковым.Корреляционную функцию случайного процесса можно определить через его энергетический спектр по теореме Винера-Хинчина [1, стр.117 –119]. эргодическим случайным процессом или не является таковым.Корреляционную функцию случайного процесса можно определить через его энергетический спектр по теореме Винера-Хинчина [1, стр.117 –119].
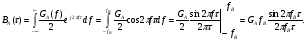
BA(τ)
GAfB
-3/2fB -2/2fB-1/2fB 0 1/2fB2/2fB3/2fB
Рис. 3.1.2. Корреляционная функция процесса A(t)
График BA(τ) приведен на рис. 3.1.2.
|
|
|
 Скачать 0.81 Mb.
Скачать 0.81 Mb.
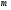 определяется двумя последними цифрами в номере зачетной книжки (98) Используя номер варианта
определяется двумя последними цифрами в номере зачетной книжки (98) Используя номер варианта 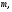 внести свои данные в табл. 1.
внести свои данные в табл. 1.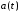 стационарного случайного процесса
стационарного случайного процесса 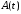 типа квазибелого шума с параметрами
типа квазибелого шума с параметрами 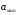 ,
,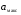 и
и 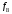 . Мгновенные значения сообщения равновероятны в интервале от значения
. Мгновенные значения сообщения равновероятны в интервале от значения 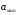 до значения
до значения 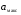 .
.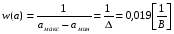
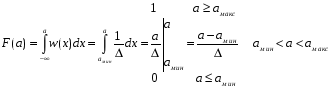
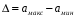 = 51,2 В.
= 51,2 В.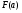 иw(a) приведены на рис. 3.1.1.
иw(a) приведены на рис. 3.1.1.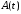
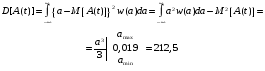
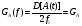 = 212,5/(2∙1,56∙104)= 6,8мВ2/Гц
= 212,5/(2∙1,56∙104)= 6,8мВ2/Гц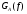
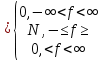
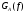
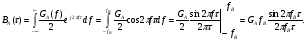




















 Федеральное
Федеральное  =56
=56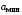 ,
, 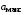 (В)
(В)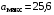 (В)
(В)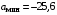 (В)
(В)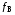
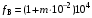 (Гц)
(Гц)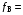 1,56 ∙10 4 (Гц)
1,56 ∙10 4 (Гц)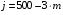
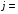 332
332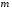
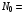 2,3∙10-7
2,3∙10-7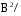 Гц
Гц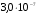
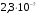
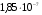
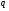 – номер тактового
– номер тактового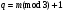
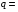 3
3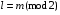
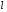
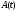 и построить график.
и построить график. 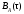 сообщения
сообщения