Курсовая работа - Экономико-математическое моделирование (с прим. Курсоваяработ а по дисциплине Экономикоматематическое моделирование

• Название: Курсоваяработ а по дисциплине Экономикоматематическое моделирование
• Дата: 15.11.2022
• Размер: 4.96 Mb.
• Имя файла: Курсовая работа - Экономико-математическое моделирование (с прим.doc
• Тип: Курсовая; #788903
• страница: 2 из 3

4. Задача о назначениях
В конкурсе на занятие пяти вакансий (V1, V2, V3, V4, V5) участвуют семь претендентов (P1, P2, P3, P4, P5, P6, P7). Результаты тестирования каждого претендента, на соответствующие вакансии, даны в виде матрицы - С (тестирование производилось по десятибалльной системе).

Определить, какого претендента и на какую вакансию следует принять, причем так, чтобы сумма баллов всех претендентов оказалась максимальной.
С =

	V1	V2	V3	V4	V5
P1	7	5	7	6	7
P2	6	4	8	4	9
P3	8	6	4	3	8
P4	7	7	8	5	7
P5	5	9	7	9	5
P6	6	8	6	4	7
P7	7	7	8	6	4

Рис.22
I. Математическая модель задачи.

1) Переменные задачи.

Ведем переменные x_ij принимающие два значения:

x_ij=0, если i-й претендент (P_i) не принимается на j-ю вакансию (V_j).

x_ij=1, если i-й претендент (P_i) принимается на вакансию (V_j).

i=1,2,...7; j=1,2,...5.

2) Ограничения на переменные задачи.

Очевидно, что все переменные задачи неотрицательные и целые числа: x_ij 0 и x_ij - целые.

Кроме того, так как каждый претендент может занять только одну вакансию и все вакансии должны быть заняты, должны удовлетворяться следующие ограничения:

, j=1,2,...7 ,

, i=1,2,...5 ,

другими словами в матрице (x_ij) суммы элементов по каждой строке и суммы элементов по каждому столбцу должны быть равны единицам. Это условие означает, что выбор претендентов должен быть таким, чтобы в матрице (x_ij), представляющей решение задачи, было бы по одной единице в каждой строке и по одной единице в каждом столбце, остальные элементы матрицы должны равняться нулю.

3) Целевая функция в задаче о назначениях.

Необходимо выбрать претендентов так, чтобы суммарное число очков, набранное ими было бы максимальным. Суммарное число набранных очков вычисляется по формуле:

;

Z=c₁₁x₁₁+c₁₂x₁₂+...+c₇₅x₇₅=7x₁₁+5x₁₂+...+4x₇₅;

Окончательная математическая модель задачи записывается так:

найти max ;

при ограничениях:

x_ij 0 и x_ij - целые числа, i=1,2,...7; j=1,2,...5;

, j=1,2,...7 ;

, i=1,2,...5 .

Таким образом, задача о назначениях есть частный случай транспортной задачи (Пример 2).
II. Решение задачи о назначениях при помощи преобразования матрицы (С).

Рассмотрим решение задачи о назначениях, в которой нужно найти min функции Z. Предварительно задачу о назначениях нужно сбалансировать. В рассматриваемом примере эта процедура выполняется добавлением двух столбцов (две фиктивные вакансии) с нулевыми результатами тестирования: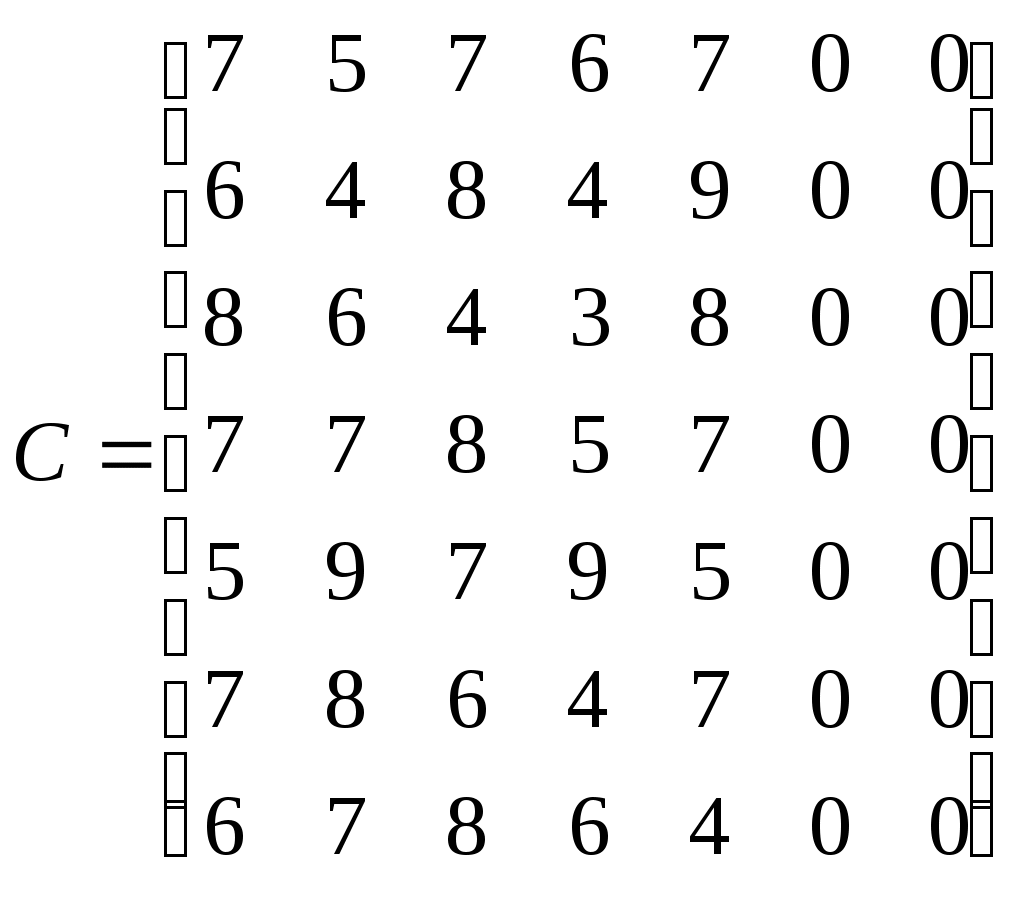



Задача нахождения минимального значения функции Z эквивалентна задаче нахождения минимума для функции 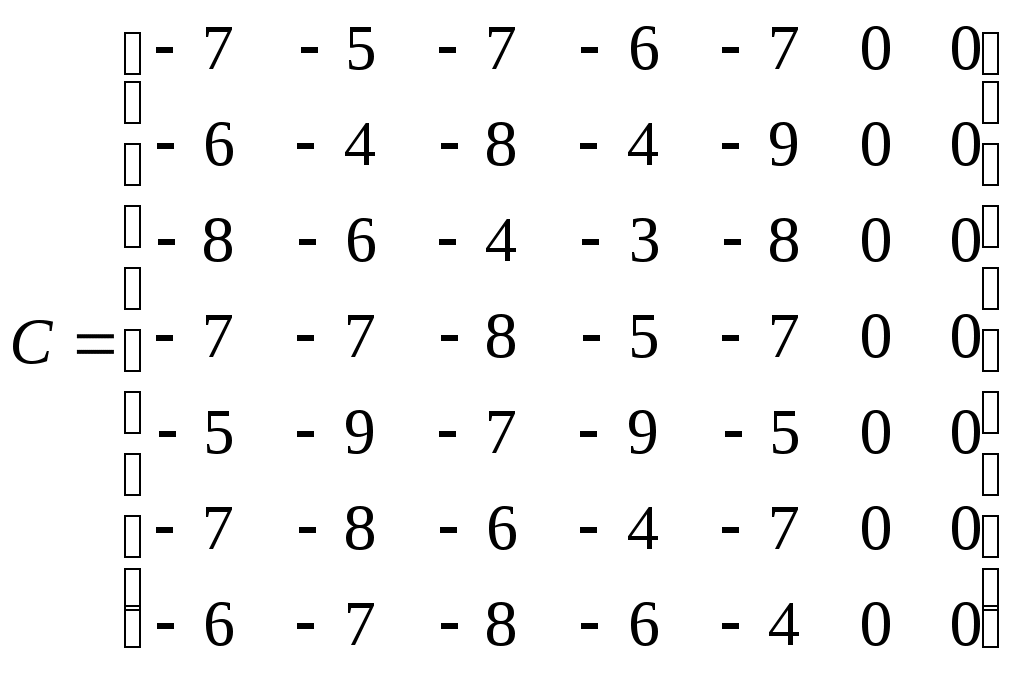, матрица (-С) имеет вид:

-

нетрудно показать, что при вычитании из всех элементов столбца или строки матрицы (С) одного и того же числа, решения x_ij при которых функция имеет минимум не меняется. Поэтому матрицу (С) преобразуем по следующему правилу. В каждой строке (С) и в каждом столбце образуют нули, вычитая минимальные элементы из соответствующих строк или столбцов. Если среди нулевых элементов матрицы (С) можно получить допустимое решение задачи, то оно является оптимальным. Напомним, что допустимым решением является такой выбор из нулей, при котором выбирается по одному нулю в каждой строке и по одному нулю в каждом столбце.

В рассматриваемом примере в каждой строке матрицы (С) нули есть (они появились в результате добавления фиктивных вакансий). Чтобы образовать нули в первых пяти столбцах матрицы (-С), определяем минимальные элементы в этих столбцах: -8, -9, -8, -9, -9 и вычитаем эти элементы из соответствующих столбцов матрицы. В результате получим следующую матрицу (рис.20):

	4	1	3	2	0	0
2	5	0	5	0	0	0
С1= 0	3	4	6	1	0	0
1	2	0	4	2	0	0
3	0	1	0	4	0	0
1	1	2	5	2	0	0
2	2	0	3	5	0	0

рис.20
Так как из нулевых элементов нельзя получить допустимое решение (в первой и шестой строках, а также в четвертой и седьмой строках нули стоят на одном и том же месте), то алгоритм продолжается следующим образом:

a) минимальным количеством горизонтальных и вертикальных прямых вычеркиваем все нули.

b) среди не вычеркнутых элементов находим минимальный элемент;

c) вычитаем минимальный элемент из всех вычеркнутых элементов;

4. 
   к элементам, стоящим на пересечении вертикальных и горизонтальных прямых, прибавляем минимальный элемент.
   

Среди множества получаемых нулевых элементов определяем допустимое решение. Если допустимое решение найти нельзя, повторяем шаги a, b, c, d снова.

Процедура вычеркивания элементов и ее результат показаны на рис.21. Минимальный среди не вычеркнутых элементов равен единице. На рис.22 показан результат после вычитания единицы из не вычеркнутых элементов и прибавления единицы к элементам, стоящим на пересечении прямых. Допустимое решение соответствует отмеченным элементам.

1	4	1	3	2	0	0
2	5	0	5	0	0	0
0	3	4	6	1	0	0
1	2	0	4	2	0	0
3	0	1	0	4	0	0
1	1	2	5	2	0	0
2	2	0	3	5	0	0

Рис.21

1	3	1	2	1	0	0
3	5	1	5	0	1	1
0	2	4	5	0	0	0
1	1	0	3	1	0	0
4	0	2	0	4	1	1
1	0	2	4	1	0	0
2	1	0	2	4	0	0

Рис.22

Перенеся полученное решение на исходную матрицу (С) (рис.23):

7	5	7	6	7	0	0
6	4	8	4	9	0	0
8	6	4	3	8	0	0
7	7	8	5	7	0	0
5	9	7	9	5	0	0
6	8	6	4	7	0	0
7	7	8	6	4	0	0

Рис.23

получим, что претенденты Р1 и Р7 попадают на фиктивные вакансии и не принимаются на работу. Р2 принимается на пятую вакансию, Р3 - на первую, Р4 - на третью, Р5 - на четвертую, Р6 - на вторую. Сумма баллов, полученная при данном решении равна: 9+8+8+9+8=42.

III.Решение задачи в процедуре EXCEL «Поиск решения»

1) Ввод данных. Переносим данные задачи в EXCEL, при этом нужно ввести 2 столбца (6-ой и 7-ой) с нулевыми значениями для сбалансирования задачи. Результаты заполнения таблицы EXCEL можно увидеть на рис.24 :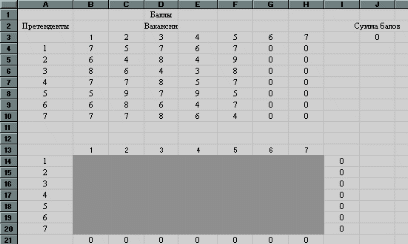


Рис.24

В ячейках B4 : F10 введены результаты тестирования претендентов, а в ячейках G4 : H10 введены нули, что соответствует фиктивным вакансиям.

Ячейки B14 : F20 являются изменяемыми ячейками для нашей процедуры.

В ячейках B21 : H21 находятся суммы значений соответствующих столбцов изменяемых ячеек. Так в ячейке B21 находится сумма ячеек B14 : B20. Аналогично в ячейках :

в С21 находится сумма ячеек С14 : С20;

в D21 находится сумма ячеек D14 : D20;

в E21 находится сумма ячеек E14 : E20;

в F21 находится сумма ячеек F14 : F20.

в G21 находится сумма ячеек G14 : G20;

в H21 находится сумма ячеек H14 : H20.

В ячейках I14 : I20 находятся суммы значений соответствующих строк изменяемых ячеек. Так в ячейке I14 находится сумма ячеек B14 : H14. Аналогично в ячейках :

в I15 находится сумма ячеек B15 : H15;

в I16 находится сумма ячеек B16 : H16;

в I17 находится сумма ячеек B17 : H17;

в I18 находится сумма ячеек B18 : H18;

в I19 находится сумма ячеек B19 : H19;

в I20 находится сумма ячеек B20 : H20.

Целевая функция заносится в ячейку J3 и вычисляется по формуле «СУММПРОИЗВ(B4:H10;B14:H20)».

2) Заполнение окна процедуры «Поиск решения»:

целевая функция : J3;

значение целевой функции : max;

изменяемые ячейки : B14 : H20;

ограничения задачи :

B21 : H21 =1 и I14 : I20 = 1(все свободные рабочие места должны быть заняты);

B14 : F20 0 (изменяемые ячейки должны иметь положительные значения).

В окне «Параметры» установить «Линейная модель», что соответствует решению задачи симплекс-методом. Результаты заполнения окна показаны на 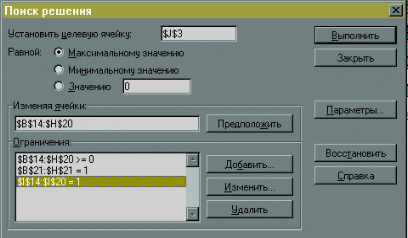рис.25:
Рис.25

3) Выполнив процедуру «Поиск решения» мы получили в первоначальной таблице следующие результаты (таблица 26):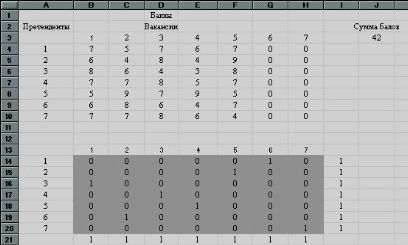


Рис.26

Эти результаты совпадают с решением задачи, полученным преобразованием матрицы (С).