расчет абсорбера. ПЗ. Курсовой проект 78 с., 1 рис., 2 табл., 7 источников
 Скачать 2.02 Mb. Скачать 2.02 Mb.
|
|
Вывод: в данном разделе мы определили объемный расход газа V = 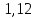 м3/с, а так же нашли стандартный диаметр м3/с, а так же нашли стандартный диаметр 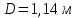 . .7 Расчет плотности орошения и активной поверхности насадки Плотность орошения (скорость жидкости) рассчитывают по формуле: 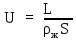 , (7.1) , (7.1)где 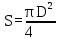 – площадь поперечного сечения абсорбера, – площадь поперечного сечения абсорбера, 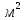 ; ;L – массовый расход поглотителя (этиленгликоль), кг/с; 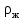 – плотность жидкости, кг/ – плотность жидкости, кг/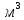 Отсюда 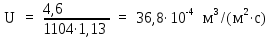 При недостаточной плотности орошения и неправильной организации подачи жидкости поверхность насадки может быть смочена не полностью. Но даже часть смоченной поверхности практически не участвует в процессе массопередачи ввиду наличия застойных зон жидкости или неравномерного распределения газа по сечению колоны. Существует некоторая минимальная эффективная плотность орошения Umin выше которой всю поверхность насадки можно считать смоченной. Для насадочных абсорберов минимальную эффективную плотность орошения Umin находим по соотношению: 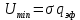 , (7.2) , (7.2)где qэф – эффективная линейная плотность орошения, м2/с.qэф =0,022· 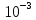 м2/с м2/сПо формуле (7.2) минимальная эффективная площадь орошения равна: 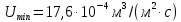 U > 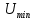 – условие выполняется. – условие выполняется. 8 Расчет коэффициентов массоотдачи Для регулярных насадок коэффициент массоотдачи в газовой фазе 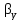 находят из уравнения: находят из уравнения: 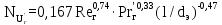 , (8.1) , (8.1)где 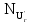 - диффузионный критерий Нуссельта для газовой фазы - диффузионный критерий Нуссельта для газовой фазы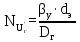 (8.2) (8.2)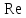 г – критерий Рейнольдса для газовой фазы в насадке; г – критерий Рейнольдса для газовой фазы в насадке;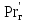 - диффузионный критерий Прандтля для газовой фазы; - диффузионный критерий Прандтля для газовой фазы; dЭ – эквивалентный диаметр насадки, м; l – высота элемента насадки, м. Тогда, учитывая выражение (8.2), находим 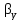 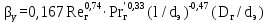 , (8.3) , (8.3)где 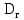 – коэффициент диффузии воды в газовой фазе (метан), м2/с. – коэффициент диффузии воды в газовой фазе (метан), м2/с.Определим критерий Рейнольдса: 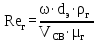 , (8.4) , (8.4)где ω – рабочая скорость газа в абсорбере, м/с; dЭ – эквивалентный диаметр насадки, м; 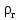 – плотность газа, кг/м3; – плотность газа, кг/м3; Vсв – доля свободного объема, м3/м3; 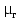 – вязкость газа, Па – вязкость газа, Па с. с.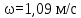 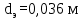 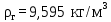 Vсв 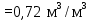 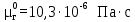 (при 0 ºС) (при 0 ºС)Приведем 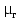 к условиям в абсорбере: к условиям в абсорбере: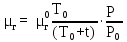 (8.5) (8.5)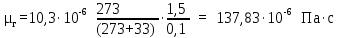 Критерий Рейнольдса согласно (8.4) равен: 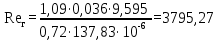 Критерий Прандтля определим по формуле: 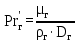 , (8.6) , (8.6)где 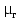 – вязкость газа, Па.с; – вязкость газа, Па.с; 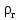 – плотность газа, кг/м3; – плотность газа, кг/м3; 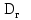 – коэффициент диффузии воды в газовой фазе, м2/с. – коэффициент диффузии воды в газовой фазе, м2/с.Коэффициент диффузии этиленгликоля в газе можно рассчитать по уравнению: 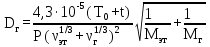 , (8.7) , (8.7)где vэт и vг – мольные объемы этиленгликоля и метана, см3/моль; МЭТ и МГ – мольные массы соответственно этиленгликоля и метана; P – давление (абсолютное), атм. Vэт и vг находим следующим образом: O=7,4 см3/атом; C=14,8 см3/атом; H=3,7 см3/атом; vэт=7,4·2+3,7·6+14,8·2=66,6 см3/моль vГ=14,8+3,7·4=29,6 см3/моль; МЭТ и МГ находим следующим образом: O=16; C=12; H=1; МЭТ=12·2+1·6+16·2=62 МГ=12+1·4=16 Подставив в формулу (8.7) найденные значения, получим 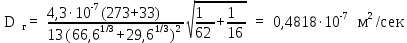 Определим критерий Прандтля по формуле (8.6): 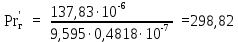 Определим коэффициент массоотдачи в газовой фазе по формуле (8.3): 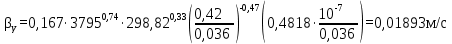 Выразим βy в выбранной для расчета размерности: 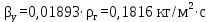 Коэффициент массоотдачи в жидкой фазе βx находят из обобщенного уравнения, пригодного как для регулярных, так и для неупорядоченных насадок: 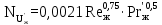 , (8.8) , (8.8)где 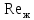 - критерий Рейнольдса для стекающей по насадке пленки жидкости; - критерий Рейнольдса для стекающей по насадке пленки жидкости;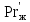 - диффузионный критерий Прандтля для жидкой фазы; - диффузионный критерий Прандтля для жидкой фазы;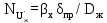 – диффузионный критерий Нуссельта для жидкой фазы. – диффузионный критерий Нуссельта для жидкой фазы.Отсюда βx (в м/с) равен: 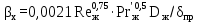 , (8.9) , (8.9)где 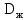 – коэффициент диффузии воды в жидкой фазе (этиленгликоль), м2/сек; – коэффициент диффузии воды в жидкой фазе (этиленгликоль), м2/сек;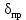 – приведенная толщина стекающей пленки жидкости, м. – приведенная толщина стекающей пленки жидкости, м.Определим критерий Рейнольдса: 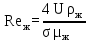 , (8.10) , (8.10)где 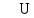 – плотность орошения, м/с; – плотность орошения, м/с;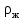 – плотность жидкости, кг/м3; – плотность жидкости, кг/м3;σ – удельная поверхность насадки, м2/м3; 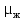 – вязкость жидкости, Па·с. – вязкость жидкости, Па·с.Плотность орошения определили по формуле (7.1): 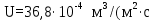 ) )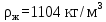 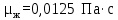 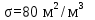 Отсюда 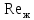 по формуле (8.10) равен по формуле (8.10) равен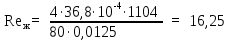 Приведенную толщину стекающей пленки жидкости определим по формуле: 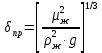 , (8.11) , (8.11)где 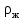 – плотность жидкости, кг/м3; – плотность жидкости, кг/м3; 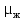 – вязкость жидкости, Па·с; – вязкость жидкости, Па·с; 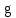 – ускорение свободного падения, м/с2. – ускорение свободного падения, м/с2.Отсюда имеем 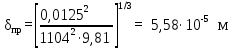 Критерий Прандтля определим по формуле: 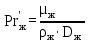 (8.12) (8.12)Коэффициент диффузии воды в этиленгликоле 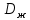 определим по формуле: определим по формуле: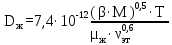 , (8.13) , (8.13)где 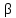 – параметр, учитывающий ассоциацию молекул растворителя; – параметр, учитывающий ассоциацию молекул растворителя; M – молекулярная масса растворителя (этиленгликоля); T – температура процесса абсорбции, К; 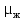 - вязкость этиленгликоля, мПа·с; - вязкость этиленгликоля, мПа·с; 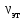 – молекулярный объем этиленгликоля. – молекулярный объем этиленгликоля.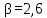 ; ;М = 12·2+1·6+16·2=62 кг/кмоль; Т = 306 К; 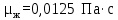 ; ; vэт=7,4·2+3,7·6+14,8·2=66,6 см3/моль Подставив значения в формулу (8.13), получим 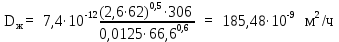 Определим критерий Прандтля по формуле (8.12): 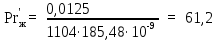 Определим критерий массоотдачи в жидкой фазе по формуле (8.9): 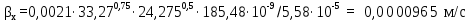 Выразим 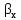 в выбранной для расчета размерности: в выбранной для расчета размерности: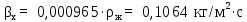 Найдем коэффициент массопередачи по газовой фазе по формуле (5.1): 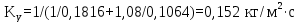 9 Расчет поверхности массопередачи и высоты абсорбера Поверхность массопередачи в абсорбере определяется по формуле: 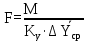 , (9.1) , (9.1)где M – производительность абсорбера по поглощаемому компоненту, кг/с; Ky – коэффициент массопередачи по газовой фазе, кг/м2  с; с; 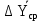 – средняя движущая сила процесса абсорбции, кг /кг. – средняя движущая сила процесса абсорбции, кг /кг.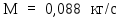 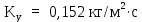 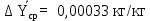 Подставив в (9.1) имеющиеся значения, получим 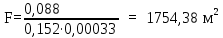 Высоту насадки, требуемую для создания этой поверхности массопередачи, рассчитаем по формуле: 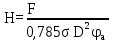 , (9.2) , (9.2)где 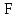 – поверхность массопередачи, м2; – поверхность массопередачи, м2; σ – удельная поверхность насадки, м2/м3; D – диаметр абсорбера, м; 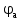 – доля активной поверхности. – доля активной поверхности.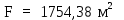 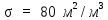 D = 1,2 м При U<0,003м3(м2  с) для регулярной насадки, доля активной поверхности, может быть определено по приближенному выражению с) для регулярной насадки, доля активной поверхности, может быть определено по приближенному выражению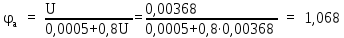 Поставив численные значения в (9.2), получим: 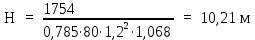 Плотность насадки составляет 670 кг/м3, для сокращения действия массы насадок на решетки в скруббере используем два последовательно соединенных скруббера и соответственно высоту насадки для каждого скруббера принимаем 5м, следовательно, общая высота насадки составит 10 м. 10 Расчет гидравлического сопротивления абсорбера Величина гидравлического сопротивления колонных аппаратов (ректификационных, абсорбционных, экстракционных) влияет на технологический режим работы аппарата. При расчете колонн определяют гидравлическое сопротивление аппарата, для того чтобы выбрать оптимальные скорости фазовых потоков, обеспечивающих эффективный массообмен. По гидравлическому сопротивлению колонны подбирают вентилятор, компрессор или насос для подачи газов и жидкостей, обеспечивающих скорость движения фаз. Величину ΔP находят по формуле: 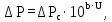 (10.1) (10.1)где 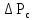 – гидравлическое сопротивление сухой (неорошаемой жидкостью) насадки, Па; – гидравлическое сопротивление сухой (неорошаемой жидкостью) насадки, Па;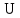 – плотность орошения, м/с; – плотность орошения, м/с;b=144 – коэффициент. Гидравлическое сопротивление сухой насадки 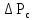 определяют по уравнению определяют по уравнению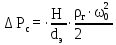 ,(10.2) ,(10.2)где λ – коэффициент сопротивления насадки; H – высота насадки, м; 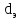 – эквивалентный диаметр насадки, м; – эквивалентный диаметр насадки, м; 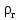 – плотность газа, кг/м3; – плотность газа, кг/м3; 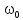 – скорость газа в свободном сечении насадки, м/с; – скорость газа в свободном сечении насадки, м/с;Скорость газа в свободном сечении насадки определим из соотношения: 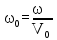 , (10.3) , (10.3)где 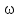 – рабочая скорость газа в абсорбере, м/с; – рабочая скорость газа в абсорбере, м/с; Vсв – доля свободного объема, м3/м3. 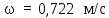 Vсв = 0,72 м3/м3 Отсюда 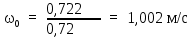 λ – коэффициент сопротивления насадки, учитывающий суммарные потери давления на трение и местные сопротивления насадки. Коэффициент сопротивления регулярных насадок находят по уравнению  ,(10.4) ,(10.4)где 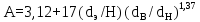 , (10.5) , (10.5)где 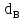 и и 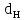 – соответственно внутренний и наружный диаметр кольца; – соответственно внутренний и наружный диаметр кольца; 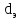 – эквивалентный диаметр. – эквивалентный диаметр.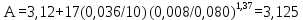 Подставляем полученное значение в (10.4): 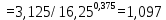 Гидравлическое сопротивление сухой насадки равно (формула 10.2) 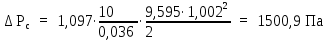 Отсюда 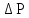 (10.1) равно: (10.1) равно: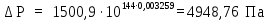 11 Расчет толщины стенки сосуда и патрубков 11.1 Определение основных геометрических параметров аппарата По заданным параметрам: высоте насадок и диаметру аппарата определяем его объем. 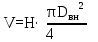 (11.1) (11.1)Рассчитываем объем аппарата по реально принятым значениям Hи Dвн: 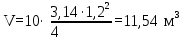 11.2 Расчет толщины стенки цилиндрической обечайки, люка и патрубков (штуцеров) 11.2.1 Расчетная толщина стенки цилиндрической обечайки 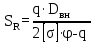 , (11.2.1) , (11.2.1)где 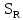 – расчетная толщина стенки обечайки, см; – расчетная толщина стенки обечайки, см;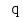 – заданное давление, кг/см2; – заданное давление, кг/см2; 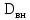 – внутренний диаметр сосуда, см; – внутренний диаметр сосуда, см; 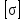 – допускаемое напряжение, кг/см2; – допускаемое напряжение, кг/см2; 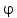 – коэффициент прочности сварного шва ( – коэффициент прочности сварного шва (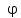 = 0,95). = 0,95).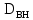 =120 см =120 смq=15 атм =0,95 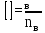 =230 кг/см =230 кг/смПодставив в (11.2.1) имеющиеся значения, получим: 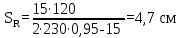 Толщина стенки обечайки S, с учетом припусков на коррозию, рассчитывается по зависимостям: 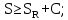 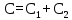 , ,где 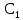 – выбранный припуск на коррозию, см; – выбранный припуск на коррозию, см; 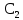 = 0,08 см – минусовой допуск на толщину листа. = 0,08 см – минусовой допуск на толщину листа.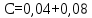 = 0,12 см = 0,12 см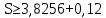 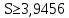 см смНоминальную толщину стенки принимаем равной 4 см, с учетом прибавок на коррозию и эрозию. 11.2.2 Толщина листа люка-лаза – 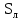 , см: , см: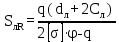 , (11.2.2) , (11.2.2)где 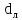 – диаметр люка-лаза выбирается в соответствии с объемом сосуда, который должен быть не меньше 1/3D см: – диаметр люка-лаза выбирается в соответствии с объемом сосуда, который должен быть не меньше 1/3D см: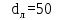 см. см.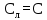 , ,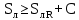 Подставив в (11.2.2) имеющиеся значения, получим: 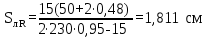 , ,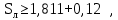 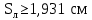 Толщину листа для люка-лаза принимаем аналогично толщине стенки обечайки 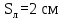 11.2.3 Толщина стенки патрубка (штуцера). Принимаем материал патрубка (штуцера) такой же, как и обечайки. Расчетная толщина стенки патрубка 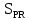 , см: , см: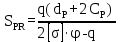 ; (11.2.3) ; (11.2.3)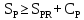 , ,где 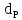 – внутренний диаметр патрубка, см; – внутренний диаметр патрубка, см;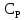 – припуск на коррозию стенки патрубка без учета минусового припуска на толщину листа, см; – припуск на коррозию стенки патрубка без учета минусового припуска на толщину листа, см;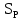 – толщина стенки патрубка с учетом припуска на коррозию, см. – толщина стенки патрубка с учетом припуска на коррозию, см.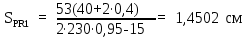 , ,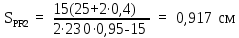 , ,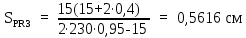 Зная значение 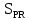 можем вычислить можем вычислить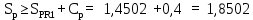 см, см,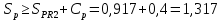 см, см,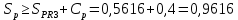 см см11.3 Проверка прочности корпуса при гидроиспытании 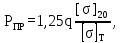 (11.3) (11.3)где 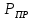 – допускаемое давление гидроиспытания, кг/см2; – допускаемое давление гидроиспытания, кг/см2;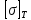 – допускаемое напряжение текучести для выбранного материала стенки сосуда при рабочей температуре, кг/см2; – допускаемое напряжение текучести для выбранного материала стенки сосуда при рабочей температуре, кг/см2;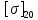 – допускаемое напряжение текучести для выбранного материала стенки сосуда при 20С, кг/см2; – допускаемое напряжение текучести для выбранного материала стенки сосуда при 20С, кг/см2;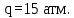 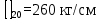 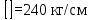 Подставив в (11.3) имеющиеся значения, получим 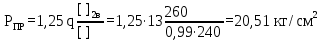 Определение значений допускаемых напряжений текучести стали, при заданной рабочей температуре, приведены на рисунке 11. 1. Расчетную температуру определяют на основании теплотехнических расчетов или результатов испытаний. За расчетную температуру стенки сосуда или аппарата принимают наибольшее значение температуры стенки. При температуре ниже 20 °С за расчетную температуру при определении допускаемых напряжений принимают температуру 20 °С. 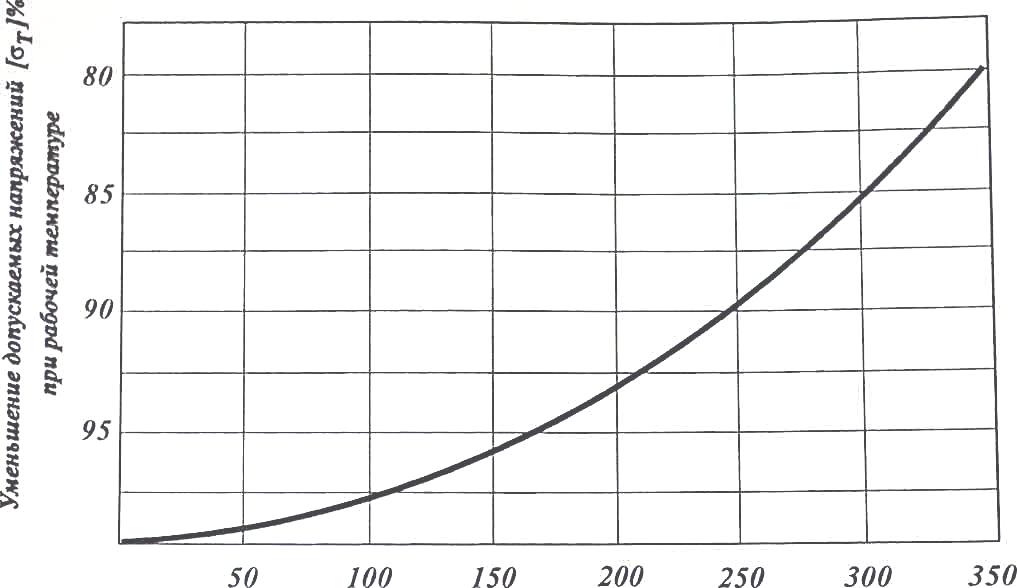 Рисунок 11.1-Определение значений допускаемых напряжений текучести стали при заданной рабочей температуре 12 Расчет днищ сосудов нагруженных внутренним избыточным давлением. Эллиптические днища. 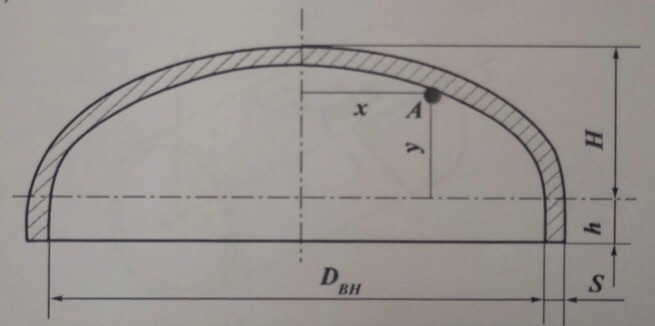 Рисунок 12.1 – Эллиптическое днище 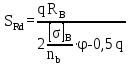 (12.1) (12.1)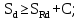 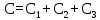 , ,где 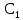 – выбранный припуск на коррозию, см; – выбранный припуск на коррозию, см; 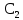 = 0,08 см - минусовой допуск на толщину листа. = 0,08 см - минусовой допуск на толщину листа.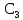 – 15% -ное утонение при штамповке, см: – 15% -ное утонение при штамповке, см: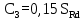 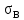 – предел прочности для выбранной марки стали, кг/см2; – предел прочности для выбранной марки стали, кг/см2;Подставив в (12.1) имеющиеся значения, получим 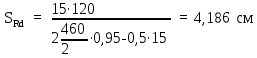 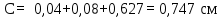 Зная значения 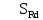 можем вычислить можем вычислить 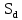 : :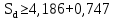 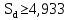 см см13 Расчет корпуса сосуда на прочность и устойчивость 13.1 Общие зависимости Рассмотрим цилиндрическую оболочку постоянной толщины под действием осесимметричных и температурных нагрузок (рисунок 13.1). 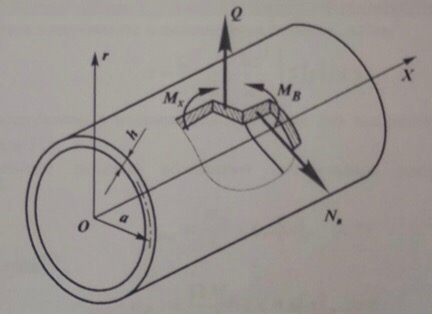 Рисунок 13.1 Силовые факторы в сечениях цилиндрической оболочки 13.1.1 Уравнение радиального прогиба оболочки Если 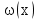 - радиальное перемещение точек срединной поверхности (положительному значению соответствует перемещение точек на окружность большего радиуса), то будем иметь следующее дифференциальное уравнение: - радиальное перемещение точек срединной поверхности (положительному значению соответствует перемещение точек на окружность большего радиуса), то будем иметь следующее дифференциальное уравнение: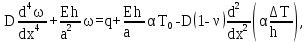 (13.1) (13.1)где 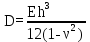 - цилиндрическая жесткость, кг-см; - цилиндрическая жесткость, кг-см;E – продольный модуль упругости материала оболочки, кг/см2 h – толщина оболочки, см; 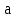 – радиус срединной поверхности, см; – радиус срединной поверхности, см;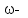 радиальное перемещение точек срединной поверхности, см; радиальное перемещение точек срединной поверхности, см;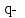 распределенная нагрузка, приложенная к срединной поверхности оболочки, кг/см2 (например, внутреннее давление); распределенная нагрузка, приложенная к срединной поверхности оболочки, кг/см2 (например, внутреннее давление);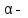 к1оэффициент линейного расширения, 1/°С; к1оэффициент линейного расширения, 1/°С;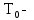 температура на поверхности оболочки; температура на поверхности оболочки;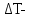 разность температур наружной и внутренней поверхности оболочки, °С; разность температур наружной и внутренней поверхности оболочки, °С;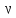 - коэффицент Пуассона, который равен для стали 20ЮЧ: - коэффицент Пуассона, который равен для стали 20ЮЧ:- легированная конструкционная сталь (низколегировання) 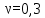 Найдем цилиндрическую жесткость: 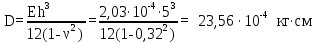 Распределение температур по толщине стенки предполагается линейным. В поперечном сечении оболочки - сечении, перпендикулярном к оси (рисунок 13.1.1), на единицу длины действуют следующие силовые нагрузки: 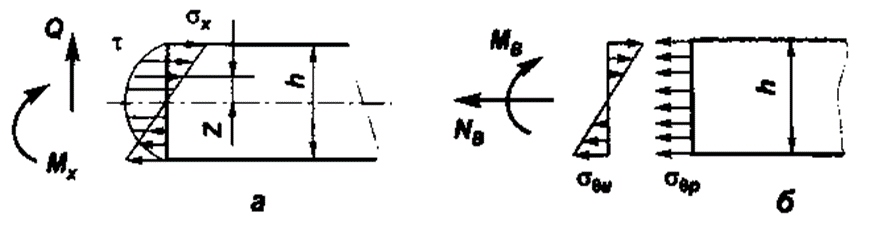 а - в поперечном сечении, б - в продольном сечении Рисунок 13.1.1- Напряжения в сечениях оболочки. 13.2 Расчет оболочек сосудов под давлением на прочность от температурных напряжений Нагрузки от температурных напряжений: Перерезывающая сила Q, кг/см: 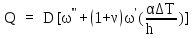 (13.2) (13.2)Подставив в (13.2) имеющиеся значения, получим 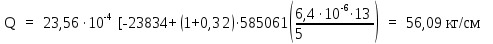 Изгибающий момент 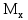 , кг-см/см: , кг-см/см: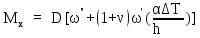 (13.3) (13.3)Подставив в (13.3) имеющиеся значения, получим 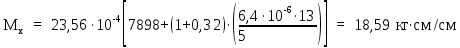 В продольном сечении (сечении, проходящем через ось) на единицу длины приходятся: -растягивающая сила 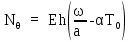 (13.4) (13.4)Подставив в (13.4) имеющиеся значения, получим 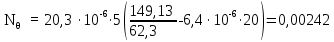 - изгибающий момент 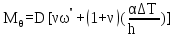 (13.5) (13.5)При отсутствии нагрева 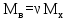 . .Напряжение изгиба в поперечном сечении распределяется по толщине стенки сосуда линейно, кг/см2 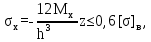 (13.6) (13.6)где 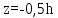 - от точки до срединной поверхности оболочки, см. - от точки до срединной поверхности оболочки, см.Касательное напряжение в поперечном сечении, кг/см2 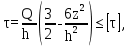 (13.7) (13.7)где 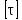 - допускаемые напряжения при срезе для выбранного материала обечайки, кг/см2. - допускаемые напряжения при срезе для выбранного материала обечайки, кг/см2.В продольном сечении возникают нормальные напряжения растяжения, кг/см2: 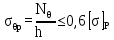 (13.8) (13.8)и изгиба, кг/см2 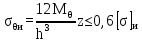 (13.9) (13.9)Нормальные напряжения в продольном сечении, кг/см2: 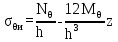 , (13.10) , (13.10)где 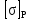 - допускаемые напряжения растяжения (сжатия) для выбранного материала, кг/см2; - допускаемые напряжения растяжения (сжатия) для выбранного материала, кг/см2;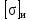 – допускаемы напряжения изгиба для выбранного материала, кг/см2. – допускаемы напряжения изгиба для выбранного материала, кг/см2.13.3 Расчет оболочек сосудов под давлением на прочность Все сосуды, работающие под давлением, можно представить как короткие оболочки (обечайки), находящиеся под внутренним избыточным давлением с закрепленными в виде глухих заделок краями (верхнее и нижнее днища). Принципиальная расчетная схема представлена на рисунке 13.3. Для этого случая решения уравнения (13.1) представляются в виде 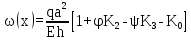 , (13.11) , (13.11)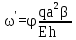 , (13.12) , (13.12)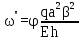 , (13.13) , (13.13)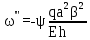 (13.14) (13.14)Подставив в (13.12) имеющиеся значения, получим: 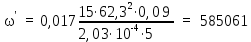 Подставив в (13.13) имеющиеся значения, получим: 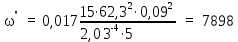 Подставив в (13.14) имеющиеся значения, получим: 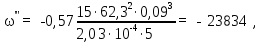 где 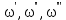 - соответственно первая, вторая и третья производные от - соответственно первая, вторая и третья производные от 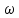 ; ;( 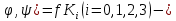 безразмерные коэффициенты, определяемые через функции Крылова (приложение А) причем ( безразмерные коэффициенты, определяемые через функции Крылова (приложение А) причем (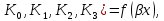 где x – длина наиболее напряженного участка сечения обечайки, см: где x – длина наиболее напряженного участка сечения обечайки, см: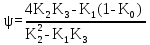 (13.15) (13.15)Зная угол 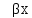 мы через функции Крылова (приложения А) определяем коэффициенты мы через функции Крылова (приложения А) определяем коэффициенты 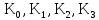 . .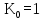 ; ;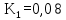 ; ;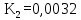 ; ;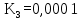 Подставив в (13.15) имеющиеся значения, получим: 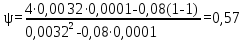 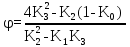 (13.16) (13.16)Аналогично, подставим в (13.16) имеющиеся значения, получим: 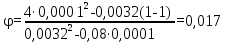 Подставив в (13.11) имеющиеся значения, получим 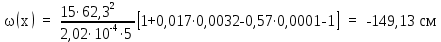 Параметр 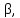 необходимый для определения этих коэффициентов, вычисляется как: необходимый для определения этих коэффициентов, вычисляется как: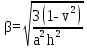 , (13.17) , (13.17)где 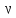 – коэффициент Пуассона. – коэффициент Пуассона.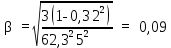 Изгибающий момент М(х), кг 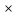 см, в опасном сечении определяется как: см, в опасном сечении определяется как: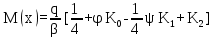 (13.18) (13.18)Подставив в (13.18) имеющиеся значения, получим: 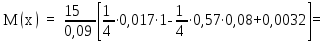 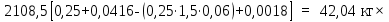 см смНапряжение изгиба в поперечном сечении распределяется по толщине стенки сосуда линейно, кг/см2 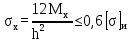 (13.19) (13.19)Подставив в (13.19) имеющиеся значения, получим: 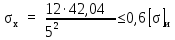 Наибольшие суммарные напряжения от изгибающих моментов и температурных нагрузок ,кг/см2; 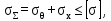 (13.20) (13.20)где 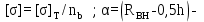 срединный радиус продольного сечения цилиндрической оболочки, см; h-принятая толщина стенки обечайки, см; D- внутренний диаметр обечайки, см; q— заданное рабочее давление в аппарате, кг/см2; срединный радиус продольного сечения цилиндрической оболочки, см; h-принятая толщина стенки обечайки, см; D- внутренний диаметр обечайки, см; q— заданное рабочее давление в аппарате, кг/см2; 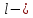 длина обечайки, см. длина обечайки, см.Подставив в (13.20) имеющиеся значения, получим: 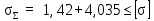 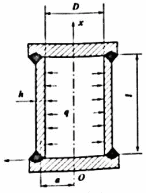 Рисунок 13.3- Принципиальная расчетная схема обечайки сосуда. 13.4 Условие устойчивости сосуда Потеря несущей способности тонкостенных конструкций может происходить в результате внезапного роста прогибов и деформаций, когда внешние нагрузки достигают критических значений. Такое явление называют потерей устойчивости, оно связано с возникновением новых форм равновесия конструкции при значительных отклонениях от первоначального положения. Потеря устойчивости может возникнуть, когда в пластинках и оболочках образуются зоны действия сжимающих напряжений. При наличии в рабочих в каком-либо одном направлении пластинки и оболочки должны подвергаться расчету на устойчивость. Обычный расчет состоит в определении запаса устойчивости 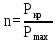 , (13.21) , (13.21)где 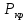 - значение силового фактора (усилия, давления, момента), при - значение силового фактора (усилия, давления, момента), прикотором возникает потеря устойчивости конструкции; 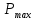 - максимальное расчетное значение силового фактора в рабочих условиях, причем большие значения используют при наличии первоначальных отклонений от правильной геометрической формы. - максимальное расчетное значение силового фактора в рабочих условиях, причем большие значения используют при наличии первоначальных отклонений от правильной геометрической формы.Расчет на устойчивость сводится к определению критических нагрузок или напряжений, приводящих к потере устойчивости Предполагают, что при расчетных критических напряжениях материал в упругом состоянии, т.е. интенсивность напряжений 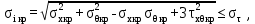 (13.22) (13.22)где 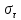 - предел текучести материала; - предел текучести материала; 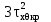 - критическое касательное напряжение, по возникновению критической неустойчивости. Этот параметр можно для упрощения расчета принимать - критическое касательное напряжение, по возникновению критической неустойчивости. Этот параметр можно для упрощения расчета принимать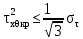 (13.23) (13.23)Если 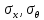 напряжения в рабочих условиях, то: напряжения в рабочих условиях, то: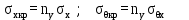 (13.24) (13.24)Если условие (13.22) не соблюдается, то в расчетных зависимостях следует заменить модуль упругости Е на касательный модуль упругости, который значительно меньше 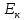 =(0,01...0,001)Е (13.25) =(0,01...0,001)Е (13.25)В приближенных расчетах можно принять, что пластическая неустойчивость наступает при работе материала конструкции в пластической области, то есть при условии 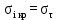 (13.26) (13.26)14 Упрощенный расчет фланцевых соединений 14.1 Типы фланцевых соединений Фланцевые соединения широко применяют в технике во всех отраслях промышленности — в оборудовании и для соединения трубопроводных магистралей. Фланцевые соединения можно подразделить на два основных типа: с не контактирующими фланцами (рис.14.1.а) и с контактирующими фланцами (рис.14.1, б). Наиболее распространен первый тип соединения (трубопроводы, сосуды и аппараты и т. п.). Они состоят из фланцев, стяжных деталей, достигающих в диаметре 200 мм и более, и, в большинстве случаев, включают уплотнительный элемент, который помещается между фланцами и может быть как пластичным, так и упругим. Соединения с контактирующими фланцами часто применяют в конструкциях, не требующих полной герметизации стыка (фланцы корпусов машин, редукторов и т. п.). Получили распространение фланцевые соединения с контактирующими стыками и с самоуплотняющимися прокладками, обеспечивающими герметичность. Такие соединения имеют меньшие габариты по сравнению с соединениями первого типа, но более сложны при изготовлении и монтаже. На рисунках 14.1- в и г показаны типы соединения фланца с патрубком (штуцером), на рисунке 14.1-д показаны типы фланцевых соединений - неконтактирущие фланцы с металлическим овальным уплотнением и мягкой прокладкой. 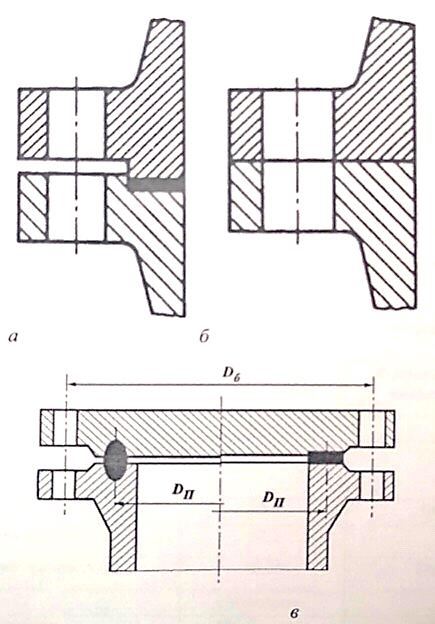 Рисунок 14.1 - Основные типы фланцев Применяют свободные фланцы (рис. 14.2), а также фланцы, изготовленные вместе с трубой (корпусом) или присоединенные к трубе с помощью сварки, резьбы, развальцовки или заклепок (рис. 14.3). 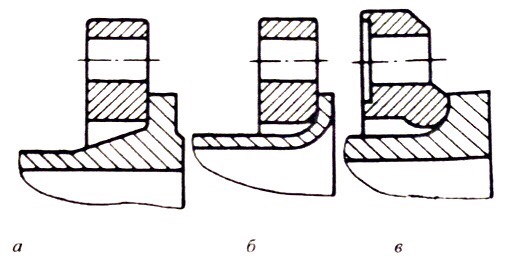 Рисунок 14.2 Свободные фланцы 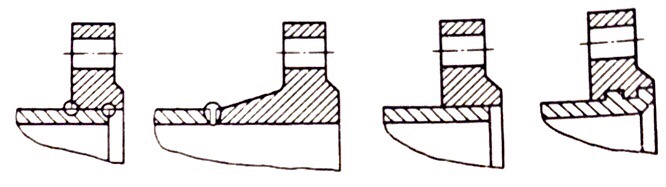 Рисунок 14.3 - Типы соединений фланцев с трубой Прокладки выполняют в виде плоского листа из паронита, картона, резины, фибры, фторопласта, меди и мягкой стали; применяют асбесто- металлические прокладки, металлические гофрированные и зубчатые, металлические линзовые прокладки и др. Во фланцевых соединениях с контактирующими фланцами используют самоуплотняющиеся прокладки в виде резиновых или металлических колец. 14.2 Упрощенный расчет фланца При проектировании аппаратов, как правило, выбирают фланцевые соединения с не контактирующими фланцами. Для предварительного выбора размеров деталей и проверки прочности фланцевых соединений с не контактирующими фланцами проводят упрощенный расчет. Основной расчетный случай Считаем, что в данной конструкции предварительно затянутое фланцевое соединение нагружено внешней продольной силой и фланцевые болты работают только на растяжение. Диаметр болта по заданному усилию нагружения выбирают, предварительно рассчитав по формуле:  где q – рабочее давление, кгс/см2; z – число болтов; 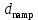 – внутренний диаметр патрубка, см; – внутренний диаметр патрубка, см;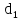 – внутренний диаметр резьбы болта, см; – внутренний диаметр резьбы болта, см;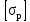 – допускаемое напряжение материала болта при растяжении. – допускаемое напряжение материала болта при растяжении.Расчётное усилие 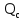 , которое действует на болты соосно оси (рис. 14.5), определим по формуле , которое действует на болты соосно оси (рис. 14.5), определим по формуле где 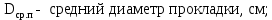 q - рабочее давление среды, кг/см2. k - коэффициент затяжки определяется по таблице 14.2. 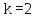 ; ;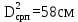 ; ;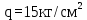 Подставив в (14.2) имеющиеся значения, получим: 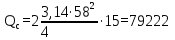 Условие прочности фланцевых болтов  где z – число болтов; d1 – внутренний диаметр резьбы принятого по справочнику болта, см; 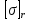 , предел текучести материала болта с учётом рабочей температуры, кг/см2. , предел текучести материала болта с учётом рабочей температуры, кг/см2.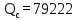 ; ;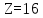 ; ;[ 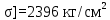 Подставив в (14.3) имеющиеся значения, получим: 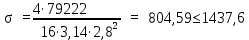 Таблица 14.2 – Определение значения коэффициента затяжки k
Расстояние между осями болтов (шаг болтов) обычно принимают при малых давлениях (q 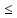 10 кг/см2) – l = (5…7) d; при больших давлениях (q 10 кг/см2) – l = (5…7) d; при больших давлениях (q 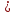 30 кг/см2) – l = (2,5…4d). Опасным сечением при расчёте на прочность фланца обычно является место перехода от фланца к трубе. 30 кг/см2) – l = (2,5…4d). Опасным сечением при расчёте на прочность фланца обычно является место перехода от фланца к трубе. Предполагается, что h 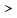 s. Уклон конического участка принимается равным 1/3 (реже 1/4 ). s. Уклон конического участка принимается равным 1/3 (реже 1/4 ).Изгибающий момент в этом сечении (на единицу длины), кг  см см где 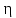 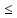 1 – коэффициент, учитывающий, что есть часть момента воспринимается поворотной деформацией фланца; 1 – коэффициент, учитывающий, что есть часть момента воспринимается поворотной деформацией фланца;l1 – расстояние от центра сечения АВ до оси болта, см; D1, – средний диаметр трубы в сечении АВ, см. 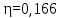 ; ;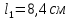 ; ;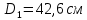 . .Подставив в (14.4) имеющиеся значения, получим: 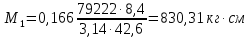 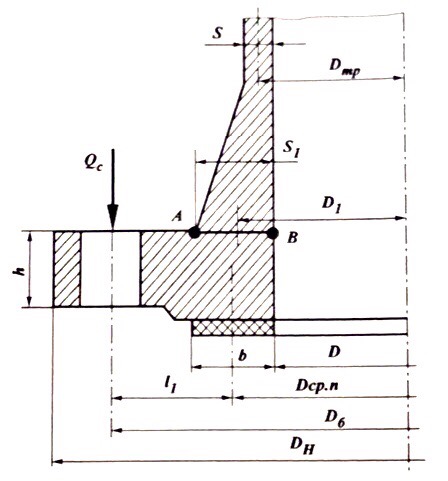 Рисунок 14.5 – К расчёту фланцевых соединений с не контактирующими фланцами Если коническая втулка (или труба) очень жесткая по отношению к фланцу и сечение АВ не поворачивается, то 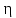 = 1. Значение = 1. Значение 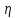 можно определить по приближённой формуле: можно определить по приближённой формуле: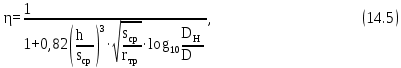 где 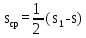 – средняя толщина трубы на коническом участке, см; – средняя толщина трубы на коническом участке, см; rтр – средний радиус трубы, см; DH и D – соответственно наружный и внутренний диаметры фланца, см. Напряжения изгиба в опасном сечении фланца (сечение АВ), кг/см2 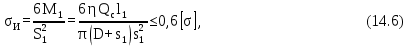 где 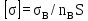 σВ – предел прочности материала фланца (при высокой температуре под σВ следует понимать предел длительной прочности), кг/см2; nB – коэффициент запаса прочности фланца, nB = 2,2. Из формулы (14.6) следует, что для снижения напряжений во фланцах целесообразно: а) приближать оси болтов к трубе (уменьшать l1), б) увеличивать толщину трубы в месте перехода к фланцу (размер S1). Однако при большой конусности (1:2) упрочнение получается чисто местным и максимум напряжений сдвигается к более тонкому сечению трубы. 14.3 Выбор уплотнений для фланцевых соединений Согласно рекомендациям выбираем неметаллические уплотнения для фланцевых узлов. |
