Проектирование редуктора на базе модели редуктора вертолёта МИ-2. Курсовой проект по деталям машин. Курсовой проект по дисциплине Детали машин
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
2.2 Проектирование конической передачи2.2.1 Определение допускаемых контактных напряженийВ связи с тем, что основные виды разрушений зубчатых передач носят усталостный характер, разрушающие напряжения в передачах определяются с использованием экспериментальных кривых выносливости. Разрушающее контактное напряжение 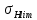 определяют по кривой контактной выносливости, пример которой показан на рисунке 2.1. определяют по кривой контактной выносливости, пример которой показан на рисунке 2.1. 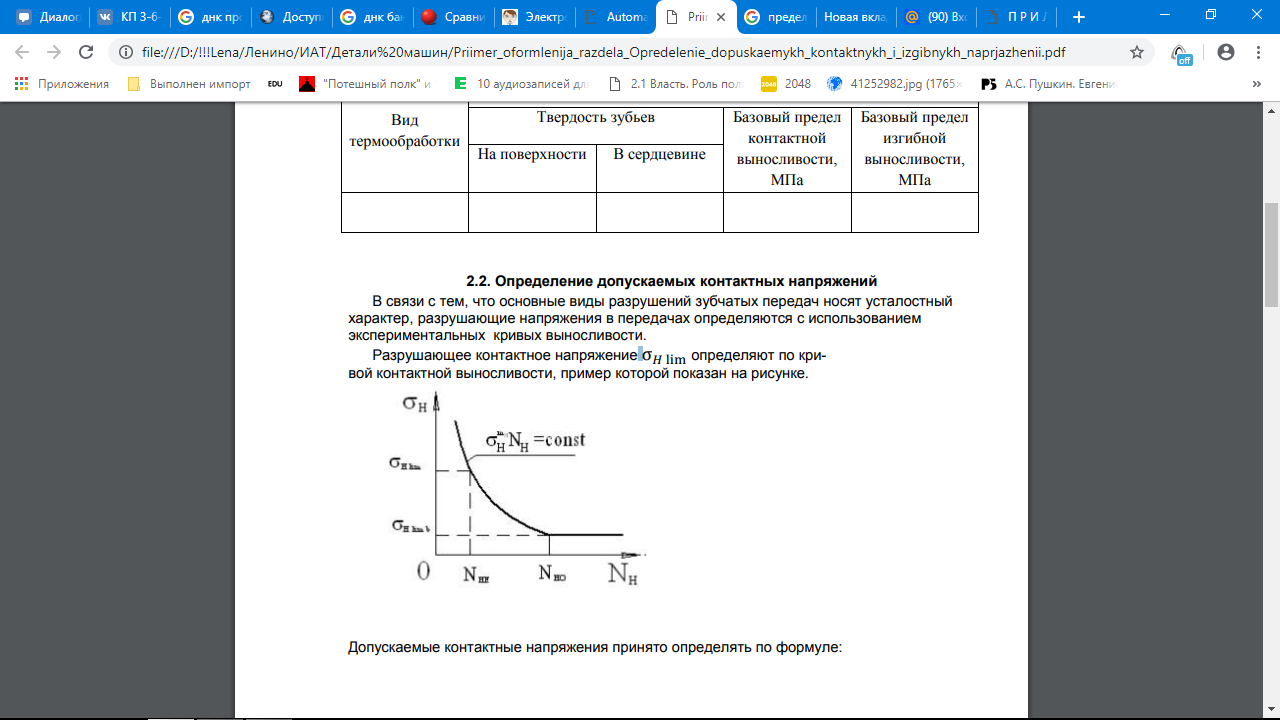 Рисунок 2.1 – Кривая контактной выносливости Допускаемые контактные напряжения принято определять по формуле: 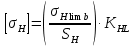 , , где  – базовый предел контактной выносливости, МПа; – базовый предел контактной выносливости, МПа;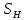 – коэффициент безопасности по контактным напряжениям; – коэффициент безопасности по контактным напряжениям;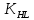 – коэффициент долговечности по контактным напряжениям. – коэффициент долговечности по контактным напряжениям.Принимаем твёрдость на поверхности зубьев HRC = 60. Базовый предел контактной выносливости согласно [1] при цементации:  Коэффициент безопасности по контактным напряжениям согласно [1] принимаем 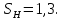 Коэффициент долговечности по контактным напряжениям определяется по формуле: 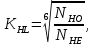 где 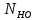 – базовое число циклов перемены контактных напряжений; – базовое число циклов перемены контактных напряжений;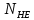 – расчетное число циклов перемены контактных напряжений. – расчетное число циклов перемены контактных напряжений.Базовое число циклов перемены контактных напряжений согласно [1] при 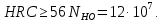 Расчетное число циклов перемены контактных напряжений для переменного режима работы определяется по формуле: 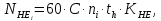 где C – число нагружений зуба за один оборот зубчатого колеса; 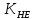 – коэффициент эквивалентности по контактным напряжениям; – коэффициент эквивалентности по контактным напряжениям;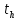 – ресурс работы передачи. – ресурс работы передачи. Коэффициент эквивалентности по контактным напряжениям определяется по следующей формуле: Коэффициент эквивалентности по контактным напряжениям определяется по следующей формуле: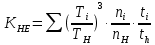 , , 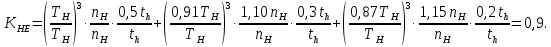 Число нагружений зуба за один оборот шестерни и колеса С=1. Расчетное число циклов перемены контактных напряжений для шестерни: 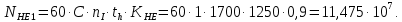 Расчетное число циклов перемены контактных напряжений для колеса: 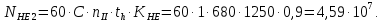 Так как  , то коэффициент долговечности по контактным напряжениям для шестерни рассчитывается по формуле: , то коэффициент долговечности по контактным напряжениям для шестерни рассчитывается по формуле: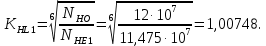 Коэффициент долговечности по контактным напряжениям для колеса: 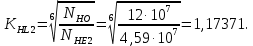 Допускаемые контактные напряжения для шестерни: 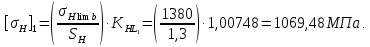 Допускаемые контактные напряжения для колеса: 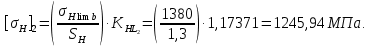 В качестве допускаемых контактных напряжений для передачи принимаем [σH] = 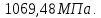  2.2.2 Определение допускаемых напряжений изгиба 2.2.2 Определение допускаемых напряжений изгибаДопускаемые напряжения изгиба принято определять по формуле: 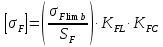 , , где 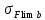 – базовый предел выносливости по изгибу, МПа; – базовый предел выносливости по изгибу, МПа;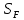 – коэффициент безопасности по напряжениям изгиба; – коэффициент безопасности по напряжениям изгиба;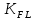 – коэффициент долговечности по напряжениям изгиба; – коэффициент долговечности по напряжениям изгиба;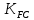 – коэффициент, учитывающий двустороннее приложение нагрузки. – коэффициент, учитывающий двустороннее приложение нагрузки.Базовый предел выносливости по изгибу согласно [1] при цементации принимаем 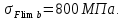 Коэффициент безопасности по напряжениям изгиба согласно [1] принимаем 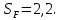 Коэффициент долговечности по напряжениям изгиба определяется по формуле: 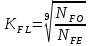 , , где  – базовое число циклов перемены напряжений изгиба; – базовое число циклов перемены напряжений изгиба;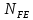 – расчётное число циклов перемены напряжений изгиба. – расчётное число циклов перемены напряжений изгиба.Базовое число циклов перемены напряжений изгиба согласно [1] при 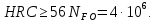 Расчетное число циклов перемены напряжений изгиба для переменного режима работы определяется по формуле: 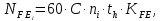 где C – число нагружений зуба за один оборот зубчатого колеса; 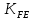 – коэффициент эквивалентности по напряжениям изгиба. – коэффициент эквивалентности по напряжениям изгиба.Коэффициент эквивалентности по напряжениям изгиба определяется по следующей формуле: 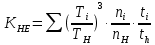 , , 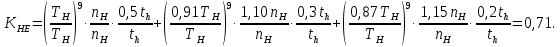 Число нагружений зуба за один оборот шестерни и колеса С=1. Расчетное число циклов перемены напряжений изгиба для шестерни:  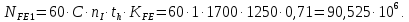 Расчетное число циклов перемены напряжений изгиба для колеса: 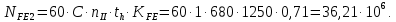 Так как 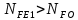 и и 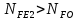 ,то коэффициент долговечности по напряжениям изгиба для шестерни и колеса ,то коэффициент долговечности по напряжениям изгиба для шестерни и колеса 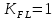 . .Коэффициент 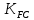 , учитывающий двустороннее приложение нагрузки, принимаем равным 1 , учитывающий двустороннее приложение нагрузки, принимаем равным 1 Допускаемые напряжения изгиба для шестерни и колеса: 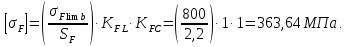 В качестве допускаемых напряжений изгиба для передачи принимаем [σF] =  2.2.3 Определение габаритных размеровОдним из основных геометрических параметров конической передачи является угол Σ между осями колес, показанный на рисунке 2, представляющий собой сумму 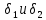 , угла делительного конуса шестерни и колеса соответственно. В данном случае угол Σ= , угла делительного конуса шестерни и колеса соответственно. В данном случае угол Σ=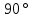 . .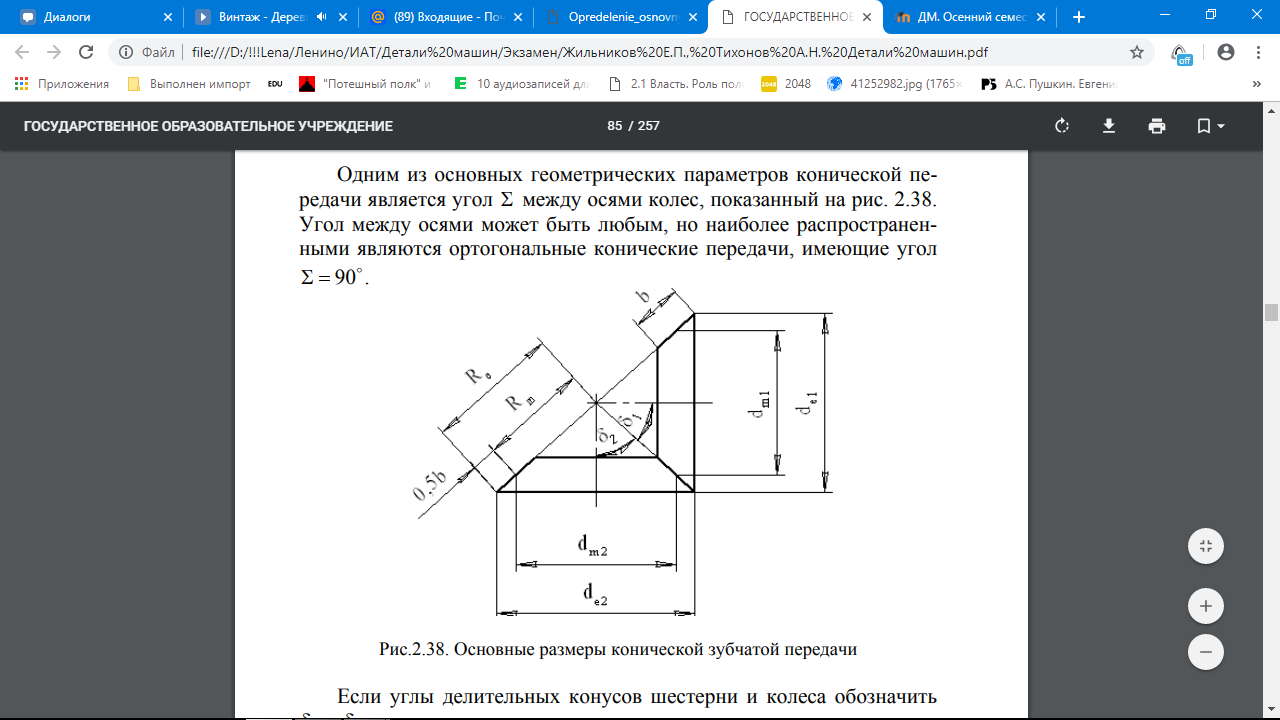 Рисунок 2.2 – Основные размеры конической зубчатой передачи Угол делительного конуса шестерни определяется по формуле: 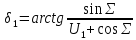 , , 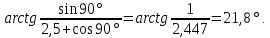  Т.к. Σ= Т.к. Σ=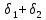 , то угол делительного конуса колеса равен: , то угол делительного конуса колеса равен: 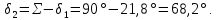 Предварительно принимаем коэффициент нагрузки по контактным напряжениям 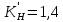 из интервала из интервала 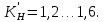 Вспомогательный коэффициент при проектировочном расчете Вспомогательный коэффициент при проектировочном расчете 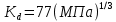 , поскольку угол наклона зубьев в среднем сечении , поскольку угол наклона зубьев в среднем сечении 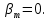 Коэффициент ширины зубчатого венца относительно среднего диаметра шестерни согласно [1] принимаем 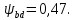 Коэффициент ширины зубчатого венца относительно конусного расстояния: 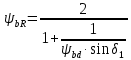 , , 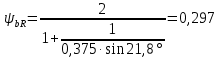 Условие 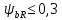 выполнено. выполнено.Средний делительный диаметр шестерни: 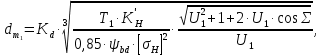 где  – вспомогательный коэффициент при проектировочном расчете, – вспомогательный коэффициент при проектировочном расчете, 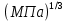 ; ; – крутящий момент на валу шестерни, Н·мм; – крутящий момент на валу шестерни, Н·мм;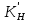 – предварительный коэффициент нагрузки по контактным напряжениям; – предварительный коэффициент нагрузки по контактным напряжениям; – допускаемые контактные напряжения для конической передачи, МПа; – допускаемые контактные напряжения для конической передачи, МПа;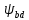 – коэффициент ширины зубчатого венца относительно среднего диаметра шестерни; – коэффициент ширины зубчатого венца относительно среднего диаметра шестерни;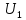 – передаточное отношение конической передачи; – передаточное отношение конической передачи;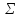 – межосевой угол, град. – межосевой угол, град. Подставив имеющиеся данные, получим: Подставив имеющиеся данные, получим: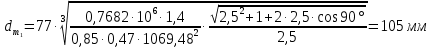 . .Определим ширину зубчатого венца по следующей формуле: 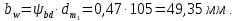 По ГОСТ 6636 примем 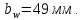 Выполним проверочный расчет. Найдем окружную скорость V: 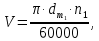 где 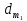 – средний делительный диаметр шестерни, мм; – средний делительный диаметр шестерни, мм; – частота вращения вала шестерни, об/мин. – частота вращения вала шестерни, об/мин.Подставим числовые значения: 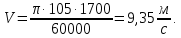 Коэффициент динамической нагрузки согласно [1] 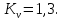 Найдем 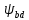 по формуле: по формуле: 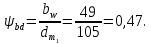 По материалам методических указаний [1] – 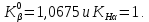 Т.к. твердость зубьев HB > 350, заключаем, что  Находим  по формуле: по формуле: Таким образом, погрешность вычисления 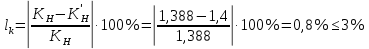
|


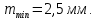 По материалам методических указаний [1] определяем коэффициент
По материалам методических указаний [1] определяем коэффициент  , поскольку степень точности конической прямозубой передачи мы выбрали равной 7.
, поскольку степень точности конической прямозубой передачи мы выбрали равной 7.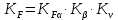 ,
, 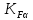 – коэффициент, учитывающий неравномерность распределения нагрузки между парами зубьев при многопарном зацеплении;
– коэффициент, учитывающий неравномерность распределения нагрузки между парами зубьев при многопарном зацеплении;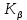 – эффективное значение коэффициента неравномерности распределения нагрузки по ширине зубчатого венца;
– эффективное значение коэффициента неравномерности распределения нагрузки по ширине зубчатого венца;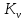 – коэффициент динамической нагрузки.
– коэффициент динамической нагрузки.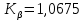 ,
, 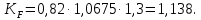
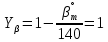 . Он равен единице, так как передача прямозубая и угол наклона зубьев в среднем сечении
. Он равен единице, так как передача прямозубая и угол наклона зубьев в среднем сечении 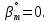
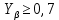 соблюдено, значит, следующим шагом мы выбираем коэффициент формы зуба
соблюдено, значит, следующим шагом мы выбираем коэффициент формы зуба 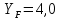 из представленного диапазона
из представленного диапазона 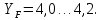
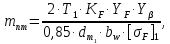
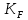 – коэффициент нагрузки при расчете по изгибным напряжениям;
– коэффициент нагрузки при расчете по изгибным напряжениям; – коэффициент формы зуба;
– коэффициент формы зуба;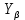 – коэффициент, учитывающий наклон зубьев;
– коэффициент, учитывающий наклон зубьев;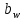 – ширина зубчатого венца, мм;
– ширина зубчатого венца, мм;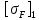 – допускаемые напряжения изгиба шестерни для конической передачи, МПа.
– допускаемые напряжения изгиба шестерни для конической передачи, МПа. Подставив числовые значения, получим:
Подставив числовые значения, получим: 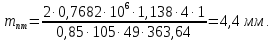
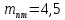 согласно [1].
согласно [1].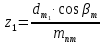 ,
, 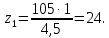
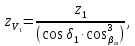
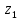 –
– 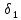 – угол делительного конуса шестерни, град;
– угол делительного конуса шестерни, град;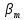 – угол наклона зубьев в среднем сечении, град.
– угол наклона зубьев в среднем сечении, град.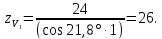
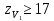 , определяем коэффициент формы зуба шестерни по материалам [1]:
, определяем коэффициент формы зуба шестерни по материалам [1]: 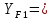 3,85.
3,85. , а значит, мы можем определить число зубьев колеса:
, а значит, мы можем определить число зубьев колеса: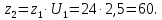
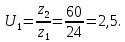
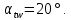
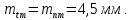

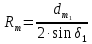 ,
, 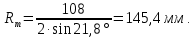
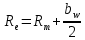 ,
, 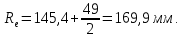
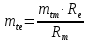 ,
, 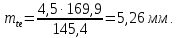
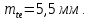
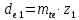 ,
, 
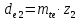 ,
, 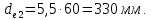
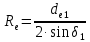 ,
, 
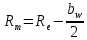 ,
, 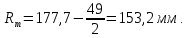
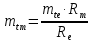 ,
, 
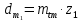 ,
, 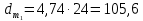 мм.
мм.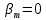 , мы можем заключить, что высота головки зуба на внешнем торце равна
, мы можем заключить, что высота головки зуба на внешнем торце равна  , а высота ножки зуба на внешнем торце равна
, а высота ножки зуба на внешнем торце равна 
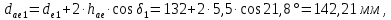
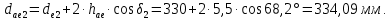
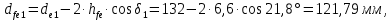
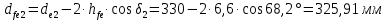

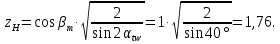
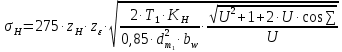 ,
, 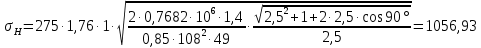 Па.
Па.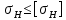 соблюдается, что означает, что условие прочности по контактным напряжениям выполняется.
соблюдается, что означает, что условие прочности по контактным напряжениям выполняется.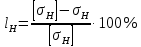 ,
, 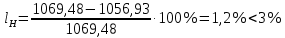
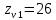 ,
, 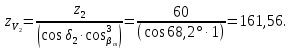
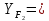 3,6.
3,6.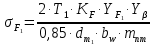

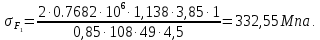
 ,
, 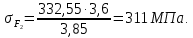
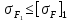 и
и 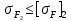 соблюдаются, а это означает, что условие прочности по напряжениям изгиба выполняется.
соблюдаются, а это означает, что условие прочности по напряжениям изгиба выполняется.
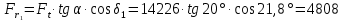 Н.
Н. 

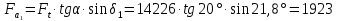 Н.
Н.