контрольная работа. КР№1. Курсовой проект по дисциплине Электротехника и электроника Тема Расчет электрических цепей постоянного и переменного тока Студент (ка) Шадеркин А. И. Фио
 Скачать 245.54 Kb. Скачать 245.54 Kb.
|
направление подготовки 15.03.02 Технологические машины и оборудование КУРСОВОЙ ПРОЕКТ по дисциплине «Электротехника и электроника» Тема Расчет электрических цепей постоянного и переменного тока Студент (ка)___Шадеркин А.И._____ ФИО Группа _Т-19205_______________ Руководитель С.Ю.Вотинова______ ___________ ____________________ оценка подпись Дата сдачи _____ __________20____г. г. Верхняя Пышма 2020г.  ЗАДАНИЕ N 1. ЗАДАНИЕ N 1.Если R=4 Ом, то эквивалентное сопротивление Rэ относительно зажимов 1-2 равно… . Решение: Составим формулу для нахождения сопротивления двух правых резисторов соединённых параллельно: Rпс= 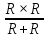 Прибавим к формуле сопротивление резистора находящегося с лева и найдем эквивалентное сопротивление: Rэ= 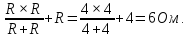 Ответ: Rэ= 6 Ом. ЗАДАНИЕ N 2. Если активная мощность приемников 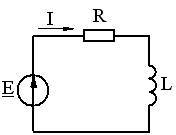 Решение: Так как Sпр=Sист то найдем реактивную мощность по формуле: 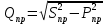 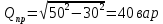 Ответ: 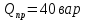 ЗАДАНИЕ N 3 Если полная мощность S=1 кВА и показания ваттметра pW=800 Вт, то реактивная мощность составит … 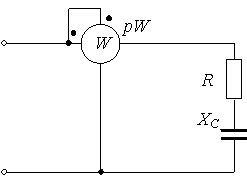 Решение: Найдем реактивную мощность по формуле: 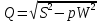 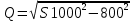 = 600 вар. = 600 вар.Ответ: Q = 600 вар. ЗАДАНИЕ N 4. Если i(t) = 4 + 8sin(t-30) А и сопротивление резистивного элемента R=5 Ом, то мгновенное значение напряжения запишется в виде … 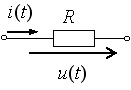 Решение: Так как I = U х R, то мгновенное значение напряжения запишется в виде: u(t) = (4 + 8sin(t-30) )R u(t) = (4 + 8sin(t-30) )  5 = 20 + 40sin(t-30) 5 = 20 + 40sin(t-30) Ответ: u(t) = 20 + 40sin(t-30) ЗАДАНИЕ 5 Запишите уравнение по закону Кирхгофа для узла А. Запишите уравнение по закону Кирхгофа для контура АДВБА 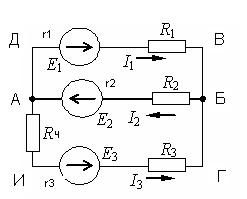 Уравнение по закону Кирхгофа для узла А: -I1+I2-I4=0 2.Уравнение по закону Кирхгофа для узла АДВБА без учета внутреннего сопротивления ЭДС: R1 ⋅ I1 + R2 ⋅ I2 = E1 + E2 3.Уравнение по закону Кирхгофа для узла АДВБА с учетом внутреннего сопротивления ЭДС: (R1 + r1) ⋅ I1 +(R2 + r2) ⋅ I2 = E1 + E2 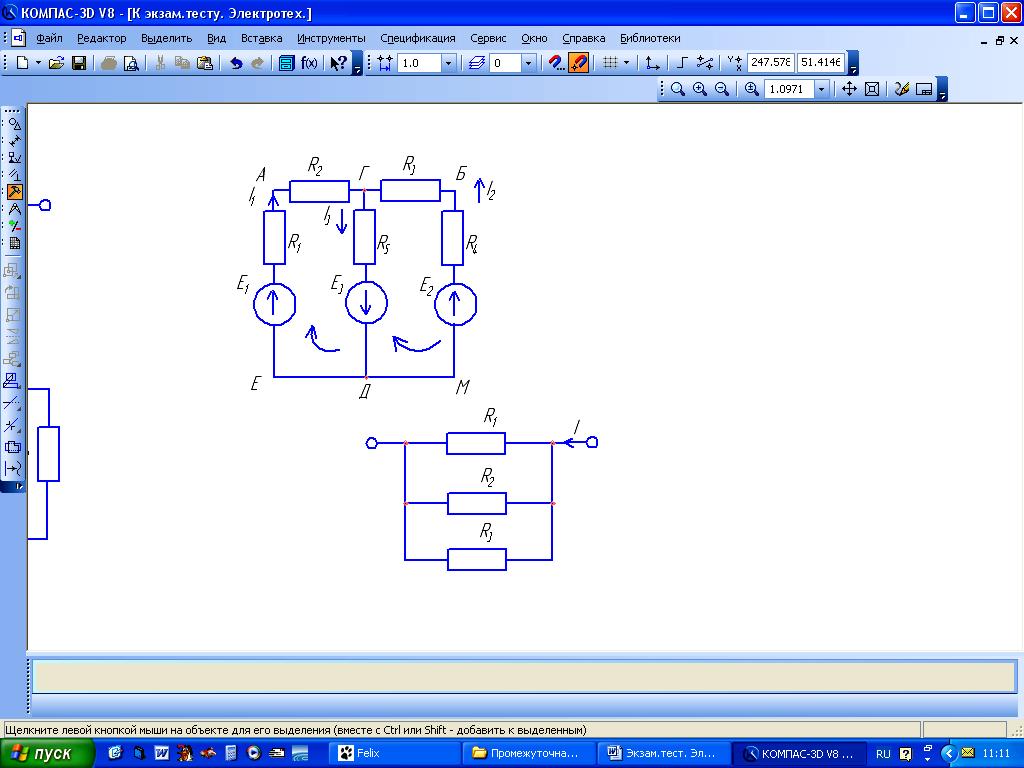 ЗАДАНИЕ 6 Найти силу тока I2, если U = 24 В, I = 2 А, R1 = 60 Ом, R3 = 40 Ом Ом. 1. Найдем RΣ RΣ= 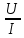 RΣ= 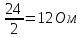 Для нахождения R2 воспользуемся формулой для параллельного соединения резисторов: 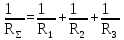 , тогда R2 найдем по формуле , тогда R2 найдем по формуле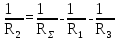 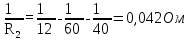 R2=24 Ом Найдем I2 по формуле: I2= 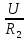 I2= 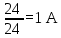 Ответ I2=1 А. ЗАДАНИЕ__9'>ЗАДАНИЕ__8'>ЗАДАНИЕ 7. В сеть переменного тока последовательно включены катушка с активным сопротивлением R =10 Ом и индуктивностью L =100 мГн и конденсатор с емкостью C=100 мкФ. Нарисовать цепь. Определить ток I в цепи и напряжения на катушке UК и конденсаторе UС при напряжении питающей сети U = 100 В, построить векторную диаграмму напряжений и тока.  R = 10 Ом L = 0.1 Гн C = 0,0001 U = 100В Um = 100 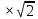 В Вi= 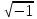 f=50 f=50 ω= 2  π π  f f  i = 2 i = 2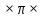 50 =314,15 50 =314,15Найдем ёмкостное сопротивление по формуле: xc= 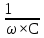 xc= 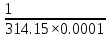 = 31,83 Ом = 31,83 ОмНайдем индуктивное сопротивление по формуле: xL=L  ω ωxL= 0.1  314,15 = 31,42 Ом 314,15 = 31,42 ОмНайдем полное сопротивление цепи по формуле: Z= 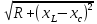 Z= 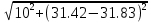 = 10,008 Ом = 10,008 ОмОпределим Im по формуле: Im= 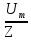 Im= 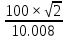 = 14,13 А = 14,13 АОпределим действующие значение тока: I=  I=  = 19.98 A = 19.98 AНайдем напряжение на конденсаторе: Uх = I  xc xcUх = 19.98  31,83 = 635,96 В 31,83 = 635,96 ВНайдем напряжение на катушке индуктивности: UL = I  xL xLUL = 19.98  31,42 = 627,77 B 31,42 = 627,77 B  Ответ: I= 19.98 А, UL= 627,77 В, Uх= 635,96 В. ЗАДАНИЕ 8 В цепи с сопротивлениями R=10 Ом, XL=50 Ом, Хс=20 Ом при токе I=2А активная мощность равна...  Найдем активную мощность по флормуле: P = I2  R RP = 22  10 = 40 Вт 10 = 40 ВтОтвет: P = 40 Вт. ЗАДАНИЕ 9 По данным задания 8 определить полное сопротивление цепи Z. Полное сопротивление рассчитаем по формуле: Z=  Z=  = 31,62 Ом = 31,62 ОмОтвет: Z= 31,62 Ом. ЗАДАНИЕ 10 Если u(t) = 60sin(t-45) В, а i(t) = 0,1sin(t+30) А, то полное сопротивление и угол сдвига фаз между напряжением и током соответственно равны … Определим сдвиг фазы между напряжением и током по формуле:  φ = -45- 30= 75 Определим полное сопротивление: 0,1sin(t+30) = Z(60sin(t-45)), тогда Z можно найти из соотношения:  = 600-1 Ом. = 600-1 Ом.Ответ: Z = 600-1 Ом, φ = 75. ЗАДАНИЕ 11. В соответствии с исходными данными выполнить расчет линейной электричемской цепи однофазного синусоидального тока со смешанным соединением активных и реактивных элементов символическим методом, а именно: Составить схему замещения электрической цепи; Рассчитать напряжения на всех участках цепи и на отдельных элементах, токи во всех ветвях схемы; Проверить правильность определения токов, используя первый закон Кирхгофа; Определить показания ваттметра; Составить баланс активных и реактивных мощностей; Построить в масштабе векторную диаграмму токов и напряжений в цепи. U13 = 55 В Ψu = 5 град f = 50 Гц L1 = 20 мГн R2 = 8 Ом С2 = 200 мкФ R3 = 6 Ом L3 = 10 Ом Составляем схему замещения электрической цепи в соответствии с исходными данными:  Рассчитаем индуктивные и емкостные сопротивления цепи: xL1= 2πf L1 xL1=2  π π 50 50 20 20 -3= 6,28 Ом -3= 6,28 ОмxL3= 2πf L3 xL3=2  π π 50 50 10 10 -3= 3,14Ом -3= 3,14ОмxС2=  xС2= 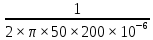 = 15,92 Ом = 15,92 ОмЗапишем полные сопротивления всех участков цепи в алгебраической и показательной формах: Z1= jxL1= xL1ej90= j6,28= 6,28 ej90 Ом Z2= R2 – jxc2= 8 - j15,92 Ом = 17.8 e-j63 Z3 = R3 + jxL3= 6 + j3,14 Ом= 6.8 ej28 Для записи показательной формы комплексного сопротивления Z2 определяем его модуль │ Z2│= 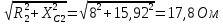 И аргумент комплексного сопротивления φ3 = arctg 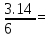 28o 28oОпределяем ток I1 в неразветвленной части цепи. Так как цепь представляет собой смешанное соединение приемников, то для нахождения тока в неразветвленной части цепи схему необходимо до общего сопротивления Zобщ Эквивалентируем сопротивление Z2 и Z3, соединенные параллельно: Z23 = 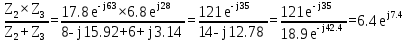 Для того, чтобы в вышеприведённой формуле поделить числитель на знаменатель, находим модуль комплексного числа в знаменателе и его аргумент. Z23=  =6,4cos7.4o+j6,4sin7,4o=6.3 + j0.82 Ом =6,4cos7.4o+j6,4sin7,4o=6.3 + j0.82 ОмОпределяем общее сопротивление цепи Zобщ В результате эквивалентного преобразования сопротивление Z2 и Z3 получаем общую схему   Теперь сопротивления Z1 и Z23 соединены последовательно, находим общее сопротивление цепи как их сумму Zобщ= Z1 + Z23 = j6,28 + 6.3 + j0.82 = 6,3 + j7,1= 9,5ej48.4 Ом Определяем ток в неразветвленной части цепи по закону Ома: I1=  = 5,8 e-j43.4= 4,2 – j3,9 A = 5,8 e-j43.4= 4,2 – j3,9 AОпределяем напряжение на всех участках цепи. U12= I1  Z1 = I1 Z1 = I1  jxL1= 5,8 e-j43.4 jxL1= 5,8 e-j43.4 6,28 ej90= 36.4ej46.6В 6,28 ej90= 36.4ej46.6ВU23= I1  Z1= 5,8 e-j43.4 Z1= 5,8 e-j43.4  = 37e-j36В = 37e-j36ВОпределяем токи во всех ветвях схемы. I2 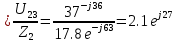 =1.9 + j0.95 А =1.9 + j0.95 АI3= 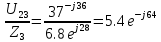 = 2.4 – j4.8 А = 2.4 – j4.8 АПроверяем правильность определения токов по первому закону Кирхгофа, составив уравнения для узла 2. I1+ I2+ I3=4,2 – j3,9 - 1.9 - j0.95 - 2.4 + j4.8 = 0 Проверка по первому закону Кирхгофа, сходится, значит, токи определены верно. Рассчитываем напряжение на отдельных элементах схемы UR2= I2  R2= R2=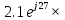 8 = 8 = 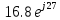 B BUXc2= I2  Xc2= Xc2=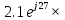 15,92 e-j90 = 15,92 e-j90 = 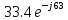 B BUR3= I3  R2= R2=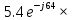 6 = 6 = 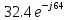 B BUXL3= I3  XL3= XL3=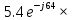 3.14 ej90 = 3.14 ej90 = 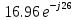 B BОпределяем полную мощность всей цепи, мощности на всех участках схемы: Sобш= U  I1 = 55ej5 I1 = 55ej5 5,8 e-j43.4= 319e-j38.4=319cos(-38.4) + j 319sin(-38.4)= 5,8 e-j43.4= 319e-j38.4=319cos(-38.4) + j 319sin(-38.4)=250 -j198.1 BA S1= U12  I1 = 36.4ej46.6 I1 = 36.4ej46.6 5,8 e-j43.4= 211.1ej3.2==211.1cos(3.2) + j 211.1sin(3.2)= 5,8 e-j43.4= 211.1ej3.2==211.1cos(3.2) + j 211.1sin(3.2)=210.8 + j11.8 BA S2= U23  I2 = 37e-j36 I2 = 37e-j36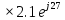 = 77.7e-j9= 77.7cos(-9) + j 77.7sin(-9)= = 77.7e-j9= 77.7cos(-9) + j 77.7sin(-9)=76.7 + j12.2 BA S3= U23  I3 = 37e-j36 I3 = 37e-j36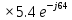 = 199.8e-j100= 199.8cos(-100) + j 199.8sin(-100)= = 199.8e-j100= 199.8cos(-100) + j 199.8sin(-100)=-34.7 - j196.8 BA 10. Составим баланс мощностей: Sобш= S1 + S2 + S3 250 -j198.1 = 210.8 + j11.8 + 76.7 + j12.2 + (-34.7 - j196.8) 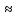 252,8 – j172,8 252,8 – j172,8Баланс мощностей сходится, следовательно, задача решена верно. Построим векторные диаграммы токов и напряжений в цепи с использованием показательных форм всех токов и напряжений, найденных в ходе решения задачи. U12 = 36.4ej46.6В U23 = 37e-j36В UR2 = 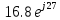 B BUXc2 = 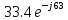 B BUR3 = 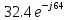 B BUXL3 = 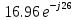 B BI1 = 5,8 e-j43.4 I2 = 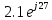 I3 = 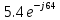 Принимаем масштаб токов mI 1 см = 2А. Принимаем масштаб для напряжений mU 1 см = 10 В. Этапы построения векторной диаграммы. Откладываем на векторной плоскости в масштабе вектора токов I2 и I3. Под углом 270 от оси абсцисс откладываем вектор тока I2 в масштабе. Под углом -640 от оси абсцисс откладываем вектор тока I3 в масштабе. 2. Строим вектор тока I1 методом переноса как сумму векторов I2 и I3. По результатам построения вектора I1, видно, что его значение совпадает с найденым расчетным путем (I1 = 5,8 e-j43.4) 3. Откладываем вектор напряжения UR2 под углом 270. Его направление совпадает с направлением вектора тока I2. От конца вектора UR2 под углом 900 с отставанием от вектора U откладываем вектор напряжения UXc2 ( 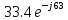 B). В результате сложения векторов UR2 и UXc2 получаем вектор U23. Как видно из векторной диаграммы, величина построенного вектора совпадает с величиной, полученной расчетным путем. B). В результате сложения векторов UR2 и UXc2 получаем вектор U23. Как видно из векторной диаграммы, величина построенного вектора совпадает с величиной, полученной расчетным путем.4. Откладываем вектор напряжения UR3 под углом -640. Его направление совпадает с направлением вектора тока I3. От конца вектора UR3 под углом 900 с опережением вектора тока I3 откладываем вектор UXL3 ( 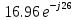 B). В результате сложения векторов UR3 и UXL3 получаем вектор U23. Как видно из векторной диаграммы, величина построенного вектора совпадает с величиной, полученной расчетным путем U23 = 37e-j36В. B). В результате сложения векторов UR3 и UXL3 получаем вектор U23. Как видно из векторной диаграммы, величина построенного вектора совпадает с величиной, полученной расчетным путем U23 = 37e-j36В.Строим вектор напряжения, приложенного к сети U13 как сумму векторов U12 и U23. Как видно из векторной диаграммы, величина построенного вектора совпадает с заданной величиной U13=55еj5 В. 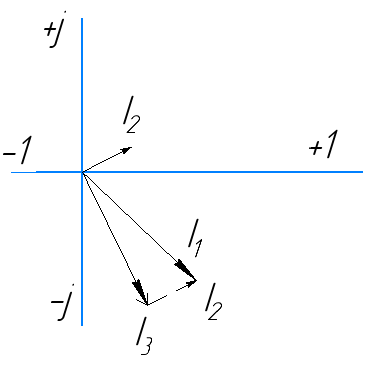 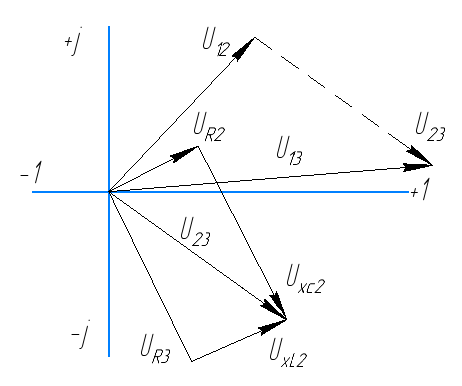 |

