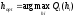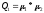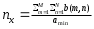Курсовая. Курсовая_Шрайбер. Курсовой проект по дисциплине корпоративные информационные системы на тему Автоматиз
 Скачать 1.34 Mb. Скачать 1.34 Mb.
|
3. РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИФильтр частиц сначала отбрасывает объекты, которые не удовлетворяют всем поставленным условиям, он рассчитывается по формулам [4] (3.1), (3.2) и (3.3).
где 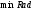 — определяемый пользователем минимальный радиус. — определяемый пользователем минимальный радиус.Затем определяется, является ли область одним объектом (колонией) или несколькими кластеризованными объектами. Чтобы быть одним объектом, он должен удовлетворять по крайней мере одному из следующих критериев рассчитываемых по формулам (3.4), (3.5) и (3.6) соответственно.
где 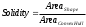 . .В противном случае принимается решение о наличии нескольких распознанных объектов. Если это один объект, он должен удовлетворять всем следующим критериям рассчитываемых по формулам (3.7), (3.8) и (3.9) соответственно.
где 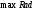 — определяемый пользователем (или рассчитанный на основе размеров изображения) максимальный радиус объекта. — определяемый пользователем (или рассчитанный на основе размеров изображения) максимальный радиус объекта.Если это кластер объектов, он должен удовлетворять всем следующим критериям рассчитываемых по формулам (3.10), (3.11), (3.12) и (3.13) соответственно.
Для разделения кластеризованных объектов - во время второго прохода обработки - вычисляют преобразование расстояния в районе 55 пикселей со значениями a=1, b=1.4, c=2.1969. Пики преобразования расстояния служат в качестве маркеров для пользовательской функции. Вкратце, функция, подобная водосбору, работает следующим образом: Все маркеры соответствуют локальным максимумам на карте расстояний. Если маркированный пиксель имеет большее или равное значение, чем соседний элемент, и соседний элемент не помечен, соседний элемент становится маркированным той же самой меткой. Кроме того, помеченным областям не разрешается расширять свою площадь над предельным значением 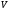 . Данный показатель рассчитывается по формуле (3.14). . Данный показатель рассчитывается по формуле (3.14).
Расстояние между исходным маркером области и любым пикселем этой области должно быть меньше значения 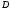 . Данный показатель рассчитывается по формуле (3.15). . Данный показатель рассчитывается по формуле (3.15).
где  - значение соответствующего пика в карте расстояний (т.е. предполагаемый радиус). - значение соответствующего пика в карте расстояний (т.е. предполагаемый радиус).Для оценки влияния числа колоний на отклонение от эталона была установлена линейная модель между отклонениями и 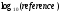 Отклонение в подсчёте каждой пластины было дано следующим образом рассчитываемым по формуле (3.16).
где 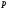 - табличный номер; - табличный номер;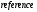 - вывод человеческого подсчёта для - вывод человеческого подсчёта для 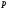 . .Абсолютные отклонения от эталона сравнивали между каждым агентом и объединённой группой людей путём проведения теста Уилкоксона. Для оценки значимости большего числа обнаруженных колоний после трансляции изображений. Для количественной оценки влияния количества пузырьков на количество обнаруженных колоний была установлена линейная модель и был выполнен t-тест на наклоне линии регрессии. Статистический анализ проводили с использованием программного обеспечения R [5]. Автоматическая многоступенчатая сегментация проходит по пространству поиска порога t интенсивности изображения I со значениями Imn пикселей, где m и n являются индексами строки и столбца соответственно. В нашем случае, t минута
где 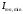 — минимальное значение пикселя; — минимальное значение пикселя;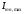 — максимальное значение пикселя. — максимальное значение пикселя.Основанная на обратной связи автоматическая сегментация границ. Этот метод был применён для адаптации порога интенсивности для сегментации. Сегментация границ весьма полезна для разделения кусков больших двоичных объектов. Он отделяет больший кусок на основе определённых исходных точек, используя информацию об интенсивности, где тёмные пиксели представляют низкую высоту, и наоборот. Однако обнаружение начальных точек может быть не совсем простым, поскольку сегментируемые объекты имеют различные максимумы интенсивности. Выбор различных значений H-максимумов преобразования H интенсивности дает разные результаты. Поэтому мы настраиваем параметр h итеративно с помощью информации, основанной на обратной связи, используя критерий качества Q1, такой, что h min ≤ h i ≤ h max . Мы берём hmin=0.10 и h max = 0.3, используя размер шага δ = 0.01. Однако диапазон параметров для него гибкий и пользователь может изменять его в соответствии со своими требованиями [6]. Параметр h адаптирован в соответствии с и рассчитывается по формуле (3.18).
где 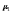 — нечёткие трапециевидные функции принадлежности для оценки ожидаемого количества; — нечёткие трапециевидные функции принадлежности для оценки ожидаемого количества;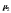 — нечёткие трапециевидные функции принадлежности для оценки ожидаемого размера. — нечёткие трапециевидные функции принадлежности для оценки ожидаемого размера.Для μ1 трапециевидные ребра равны (p1, p2, p3, p4) = (1, nx, 2nx, 3nx - 1). Переменная n x извлекается с использованием размера A i большого двоичного объекта b i, имеющего пиксельные значения, равные b (m, n) (m и n-индексы строк и столбцов соответственно), они отражены в формуле (3.10).
А μ2 - трапециевидная функция принадлежности для распределения размеров с рёбрами (p1, p2, p3, p4) = (0.5a min , a min , 2a min , max (2a min, a max )). где Q1 (hi) - качество результата сегментации в каждом hi . Всё это подробно объясняет адаптацию параметров на основе обратной связи сегментации. |

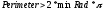 ,
,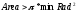 ,
,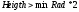 ,
,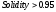 ,
,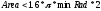 ,
,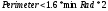 ,
,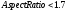 ,
,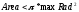 ,
,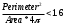 ,
,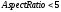 ,
,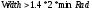 ,
,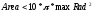 ,
,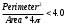 ,
, ,
,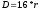 ,
,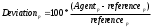 ,
,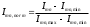 ,
,