Основы построения инфокоммуникационных систем и сетей. Курсовой проект по дисциплине Основы построения инфокоммуникационных систем и сетей Расчет основных параметров системы пдс
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
Федеральное агентство связи Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный университет телекоммуникаций и информатики» (ФГОБУ ВПО «СибГУТИ») Курсовой проект по дисциплине «Основы построения инфокоммуникационных систем и сетей» «Расчет основных параметров системы ПДС» Новосибирск, г. Содержание Стр. 1. Кодирование в системах ПДС 3 1.1 Классификация кодов 4 1.2 Эффективное кодирование 6 1.3 Корректирующее кодирование 7 1.4 Решение задач 9 2. Устройства преобразования сигналов в системах ПДС 16 2.1 Типы преобразований, используемых в устройствах преобразования сигналов в системах ПДС 16 2.2 Методы регистрации 19 2.3 Решение задачи 22 3. Синхронизация в системах ПДС 24 3.1 Классификация систем поэлементной синхронизации 24 3.2 Поэлементная синхронизация с добавлением и вычитанием импульсов (принцип действия) 26 3.3 Параметры системы синхронизации с добавлением и вычитанием импульсов 28 3.4 Решение задачи 30 4. Системы ПДС с ОС 33 4.1 Классификация и принцип работы систем с обратной связью 33 4.1.1 Системы с информационной обратной связью 34 4.1.2 Системы с решающей обратной связью 35 4.2 Решение задачи 38 Список литературы 40 Кодирование в системах ПДС В общем случае под информацией понимают совокупность сведений о каких-либо событиях, явлениях или предметах. Сообщение - это информация, представленная в определенной конкретной форме. Одна и та же информация может быть передана с помощью разных сообщений. Информация, содержащаяся в сообщении, передается получателю по каналу передачи дискретных сообщений (ПДС). Рассмотрим основные характеристики тракта передачи, в состав которого входят канал ПДС, источник (ИС) и получатель (ПС) дискретных сообщений. Источник дискретных сообщений характеризуется алфавитом передаваемых сообщений A. Пусть объем этого алфавита (число символов алфавита) K, а вероятность выдачи символа ai 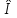 A (1 A (1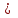 i i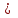 K) равна p(ai). K) равна p(ai).Количество информации в сообщении (символе) определяется в битах - единицах измерения количества информации: I(ai) = 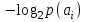 . .Среднее количество информации H(A), которое приходится на одно сообщение источника независимых сообщений: 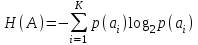 . .Определенное таким образом среднее количество информации называется энтропией источника дискретных сообщений. Энтропия максимальна, если символы источника появляются независимо и с одинаковой вероятностью. Среднее количество информации, выдаваемое источником в единицу времени, называют производительностью источника: H’(A)=H(A)/T (бит/с), где T - среднее время, отведенное на передачу одного символа (сообщения). Для каналов передачи дискретных сообщений вводят аналогичную характеристику - скорость передачи информации по каналу R. Она определяется количеством бит, передаваемых в секунду. Максимально возможное значение скорости передачи информации по каналу называется пропускной способностью канала и обозначается C. Сообщение, поступающее от источника, преобразуется в сигнал, который является его переносчиком в системах ПДС. На приемной стороне сигнал преобразуется в сообщение. Система ПДС обеспечивает доставку сигнала из одной точки пространства в другую с заданными качественными показателями. Структурная схема системы ПДС изображена на рис. 1.1 Источник и получатель сообщений вместе с преобразователем сообщения в сигнал в состав системы ПДС не входят. 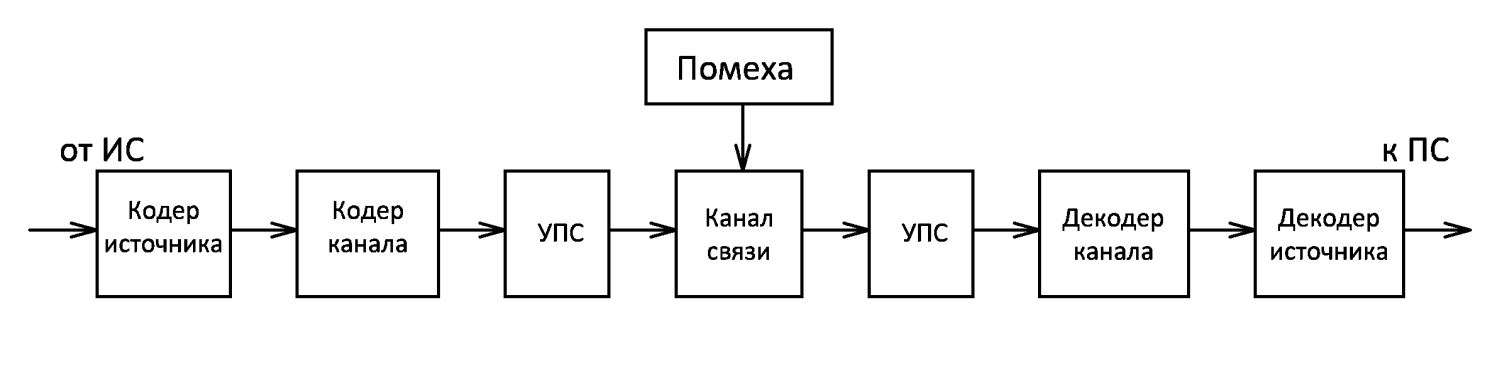 Рисунок 1.1 - Структурная схема системы ПДС 1.1 Классификация кодов Помехоустойчивые или корректирующие коды делятся на блочные и непрерывные. К блочным относятся коды, в которых каждому символу алфавита сообщений соответствует блок (кодовая комбинация) из n(i) элементов, где i - номер сообщения. Если n(i)=n, т.е. длина блока постоянна и не зависит от номера сообщения, то код называется равномерным. Такие коды чаще применяются на практике. Если длина блока зависит от номера сообщения, то блочный код называется неравномерным. В непрерывных кодах передаваемая информационная последовательность не разделяется на блоки, а проверочные элементы размещаются в определенном порядке между информационными. Проверочные элементы в отличие от информационных, относящихся к исходной последовательности, служат для обнаружения и исправления ошибок и формируются по определенным правилам. Равномерные блочные коды делятся на разделимые и неразделимые. В разделимых кодах элементы разделяются на информационные и проверочные, занимающие определенные места в кодовой комбинации. В неразделимых кодах отсутствует деление элементов кодовых комбинаций на информационные и проверочные. Разделимые коды делятся на систематические или линейные и несистематические или нелинейные. Линейные коды получили свое название потому, что их проверочные элементы представляют линейные комбинации информационных элементов. Большую и важную подгруппу линейных кодов образуют циклические коды. Линейные коды реализуются наиболее просто, что привело к их широкому использованию в УЗО. Для линейного кода применяется обозначение (n, k) - код, где n - число элементов в комбинации; k - число информационных элементов. Нелинейные коды характеризуются наличием двух или более систем проверок внутри каждой кодовой комбинации. Наиболее часто используются проверки на чётность числа единиц и нулей в разрешенных кодовых комбинациях. К основным параметрам кодов относятся: Значность кода n – количество элементов в кодовой комбинации. Самая малая значность 4, n = 5,6,7,8,9… Кодовое расстояние dmin , dmin - выявляется при попарном сравнении всех кодовых комбинаций и равняется наименьшему числу несовпадающих при сравнении разрядов. Если dmin =1 код называется простым. И от этого кода мы не сможем отследить выявление ошибок и исправления. Кратность обнаружения ошибки. Минимальное кодовое расстояние 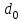 и гарантированно обнаруживаемая кратность ошибок связаны соотношением: и гарантированно обнаруживаемая кратность ошибок связаны соотношением:  . .Кратность исправления ошибки: 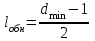 Избыточность кода: 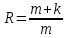 , , где m – количество информации элементов в кодовой комбинации или блоке, блок – совокупность кодовых комбинаций, k – количество дополнительных кодовых элементов в комбинации или блоке. Число возможных кодовых комбинаций. Число возможных комбинаций равно mn. Примером такого кода является пятизначный код Бодо, содержащий пять двоичных элементов (m=2, n=5). Число возможных кодовых комбинаций равно 25=32, что достаточно для кодирования всех букв алфавита. 1.2 Эффективное кодирование Статистическое (эффективное) кодирование используется с целью увеличения скорости передачи информации (устранение избыточности в сообщении). Идея оптимального статистического кодирования заключается в том, что для передачи сообщений используется неравномерный код (например, код Шеннона-Фано, код Хаффмана). Сообщения, имеющие большую вероятность, представляются в виде коротких комбинаций, а реже встречающимся сообщениям присваиваются более длинные комбинации. Такое кодирование приводит к увеличению производительности источника. Результаты кодирования тем лучше, чем более длинные кодовые комбинации первичного кода применяются для статистического кодирования. Код, обладающий тем свойством, что некое более короткое слово не является началом другого более длинного слова кода называется префиксным. Графическое представление множества кодовых слов выглядит в виде кодового дерева. Каждому узлу будет соответствовать двоичная кодовая комбинация, являющаяся узлом от корня до соответствующего узла. Рассмотрим метод Хаффмана, если имеется дискретный источник, объёмом алфавита К и заданны вероятности: P(a1)... P (ak). Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму: 1) сообщения сортируются в порядке убывания вероятностей 2) два самых маловероятных сообщения объединяются: 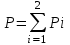 ; ;3) шаги (1) и (2) повторяются до получения единственного сообщения с Р=1; 4) строится дерево, и проставляются комбинации. 1.3 Корректирующее кодирование Целью помехоустойчивого кодирования является обнаружение и (или) исправление ошибок в кодовых словах, возникших при передаче информации по каналу с шумом. Коррекция искажений возможна за счёт введения избыточности в систему передачи. Каждому символу исходного алфавита сообщений объема Na поставим в соответствие n-элементную двоичную последовательность (кодовую комбинацию). Возможное (общее) число последовательностей длины n составляет N0=2n. Для обнаружения (исправления) на приеме ошибок должно соблюдаться условие Na<N0. Если Na=N0, то все возможные последовательности n-элементного кода используются для передачи или, как говорят, являются разрешенными. Полученный таким образом код называется простым, т.е. неспособным обнаруживать (исправлять) ошибки. Рассмотрим циклические коды. В основе построения циклических кодов лежит представление кодовых комбинаций в виде полиномов. Так, n - элементная кодовая комбинация записывается в виде: F(x)=an-1 xn-1 + an-2 xn-2 +...+ a1 x + a0, где коэффициенты ai равны 0 или 1, причем ai = 0 соответствует нулевым элементам комбинации, а ai = 1 - ненулевым. Наивысшая степень полинома на единицу меньше числа элементов кодовой комбинации. При построении комбинаций циклического кода часто используют операции сложения полиномов и деления одного полинома на другой. Так, сложение полиномов производится по обычному правилу, за исключением операции сложения, которое заменяется операцией суммирования по модулю два. Разрешенные комбинации циклического кода обладают двумя очень важными отличительными признаками: циклический сдвиг элементов разрешенной кодовой комбинации дает также разрешенную комбинацию циклического кода. Все разрешенные кодовые комбинации делятся без остатка на полином P(x), называемый образующим. Эти свойства используются при построении циклических кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок. Найдем алгоритм построения разрешенных кодовых комбинаций циклического кода по заданным комбинациям исходного простого кода, удовлетворяющих перечисленным выше условиям. Полином Q(x), соответствующий k-элементной комбинации простого кода, умножаем на 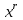 . Умножение Q(x) на . Умножение Q(x) на 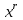 необходимо, чтобы сдвинуть информационные элементы на r разрядов влево и тем самым высвободить справа r разрядов для записи проверочных элементов. Определяем проверочные элементы в виде остатка R(x) от деления произведения Q(x) необходимо, чтобы сдвинуть информационные элементы на r разрядов влево и тем самым высвободить справа r разрядов для записи проверочных элементов. Определяем проверочные элементы в виде остатка R(x) от деления произведения Q(x)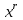 на образующий полином P(x) степени r. Проверочные элементы прибавляем к Q(x) на образующий полином P(x) степени r. Проверочные элементы прибавляем к Q(x)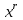 . В результате получаем кодовую комбинацию n-элементного циклического кода: . В результате получаем кодовую комбинацию n-элементного циклического кода: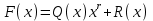 . . Так как максимальная степень остатка всегда, по крайней мере, на единицу меньше степени образующего полинома, ясно, почему степень образующего полинома выбирается равной числу проверочных элементов r. При таком способе построения комбинаций циклического кода первые k элементов являются информационными, а последующие r - проверочными, т.е. код является разделимым. В циклическом коде остаток от деления R(x) играет роль синдрома. Для определения синдрома следует разделить принятую комбинацию на образующий полином. Если все элементы приняты без ошибок, то остаток равен нулю. Наличие ошибок приводит к тому, что остаток не равен нулю. По виду остатка можно определить ошибочные элементы и исправить их. 1.4 Решение задач Задача №1. Запишите последовательность на выходе кодера Хаффмана для алфавита {A} с вероятностями {p}, если передавалась соответствующая последовательность. Дано:
| ||||||||||||||||||||||||||||||
