Курсовой проект по дисциплине Прикладная механика Студенту Елину К. А. Эп151 Тема проекта Сложное сопротивление статической определимых стержневых систем (расчет ствола и траверсы опоры)
 Скачать 115.82 Kb. Скачать 115.82 Kb.
|
      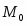 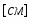    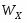   Министерство образования и науки Российской Федерации Министерство образования и науки Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего образования «Забайкальский государственный университет» (ФГБОУ ВО «ЗабГУ») Кафедра сопротивления материалов и механики Курсовой проект Чита 2017 Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Забайкальский государственный университет» (ФГБОУ ВО «ЗабГУ») Кафедра сопротивления материалов и механики ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовому проекту по «Прикладной механике» На тему: «Сложное сопротивление статической определимых стержневых систем (расчет ствола и траверсы опоры)» Проектировал: студент группы ЭП-15-1 Елин К.А. Руководитель проекта : Шадрин В.А. Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Забайкальский государственный университет» (ФГБОУ ВО «ЗабГУ») Кафедра сопротивления материалов и механики ЗАДАНИЕ на курсовой проект по дисциплине: «Прикладная механика» Студенту: Елину К. А. ЭП-15-1 Тема проекта: «Сложное сопротивление статической определимых стержневых систем (расчет ствола и траверсы опоры)» Технические условия: Вариант №8; Стержневая схема опоры ( форма поперечного сечения) № 2; 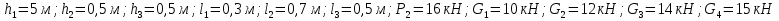 Рекомендуемая литература :
Графическая часть на ___________________листах Дата выдачи задания: «___» _________20__ г. Дата представления руководителю: «___» ______________ 20__ г. Руководитель курсового проектирования : Шадрин В. А. Подпись студента _______________________ Реферат Отчет 26 с., 1 кн., 7 рис., 3 табл., 5 источников, 1 прил. БАЛКА, ОПОРА, ТРАВЕРСА, НАГРУЗКА, ОПАСНОЕ СЕЧЕНИЕ, ЭПЮР, СОСТАВНОЕ СЕЧЕНИЕ, СПЛОШНОЕ СЕЧЕНИЕ, РАВНОВЕСИЕ, ПОПЕРЕЧНЫЙ ПРОСКИЙ ИЗГИБ, ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ, ГИБКОСТЬ. Объектом исследования являются опоры ЛЭП. Цель работы – рассчитать сплошное и составное сечение опоры, траверсу ЛЭП. В процессе работы использовалась теория вертикальных и горизонтальных стержней: плоского поперечного изгиба, устойчивости прямолинейной формы равновесия, продольно-поперечного изгиба. Полученные результаты позволили выбрать наиболее оптимальную конструкцию, то есть форму поперечного сечения, стержня опоры с экономической и технической точек зрения. Основные конструктивные и технико-эксплуатационные показатели: высокая прочность опоры при высоких внешних воздействиях, а следовательно повышение надежности электро снабжения в целом. Степень внедрения– стержневые опоры, имеющие составное сечение, применяются в создании современных ЛЭП. Опоры, имеющие составную конструкцию, имеют наиболее высокую прочность, меньшую массу и рекомендованы к внедрению во всех сферах электроэнергетики. Обе опоры могут применяться в электроснабжении промышленных предприятий и городов, а также в передачи электроэнергии на большие расстояния. Экономическая эффективность данной работы состоит в экономии на материале в производстве опоры, но при этом сохраняется её прочность при воздействии внешних сил и приложенных к траверсе нагрузок. Прогнозные предложения о развитии опор ЛЭП: наибольшую прочность составляет опора, имеющая составное поперечное сечение и элементы стержня ( например, двутавровые балки), которые соединены соединительными планками, расположенными под углом  и и  к плоскости поверхности земли. к плоскости поверхности земли.Содержание Введение 7 Условные задания 8 1. Расчет на прочность составного ствола опоры 9 1.1 Расчет реакций и построение эпюр 9 1.2 Выбор швеллера составного сечения 12 1.3 Расчет стержня АВ на устойчивость 14 1.4 Определение расстояния «а» и «b» 15 2. Расчет на прочность сплошного ствола опоры 17 2.1 Расчет диаметров: внешнего-D и внутреннего-d, сплошного сечения ствола опоры 17 2.2 Проверка стержня АВ на устойчивость 19 2.3 Сравнение веса сечений 20 3. Расчет траверсы из двух равнополочных углов 21 3.1 Нахождение реакций в шарнирах и построение эпюр изгибающих моментов 21 3.2 выбор уголка 21 3.3 Проверка на устойчивость 22 Заключение 24 Список литературы 25 Приложение 26 Введение Тема курсовой работы: «Сложное сопротивление статически определимых систем (расчет ствола опоры и траверсы опоры)». Каждая стержневая система ( на рис.1.1 показана плоская стержневая система) включает вертикальный прямой стержень  высота высота  (ствол опоры). Соединение стальных стержней с помощью сварных швов ( на сварке). Вертикальный стержень (ствол опоры). Соединение стальных стержней с помощью сварных швов ( на сварке). Вертикальный стержень  внизу в точке внизу в точке  закреплен неподвижно к фундаменту (земле)(защемлен)., напоминает консольную балку, которая расположена не горизонтально, как обычно, а вертикально, перпендикулярно к земле. При плоском поперечном изгибе стержня закреплен неподвижно к фундаменту (земле)(защемлен)., напоминает консольную балку, которая расположена не горизонтально, как обычно, а вертикально, перпендикулярно к земле. При плоском поперечном изгибе стержня  в нижней точке в нижней точке  не поворачивается. не поворачивается.Задание включает в себя две задачи: стальной вертикальный стержень  имеет составное или сплошное поперечное сечение с двумя осями симметрии, форма сечения имеется на рис.1.1 б,в. Составное сечение конструируется из четырех не равнополочных уголков: сортамент стали по ГОСТ 8510-72, соответственно имеет две ветви, расстояние между которыми «а» (рассчитывается). Обе ветви сечения связаны между собой по вертикали вдоль стержня имеет составное или сплошное поперечное сечение с двумя осями симметрии, форма сечения имеется на рис.1.1 б,в. Составное сечение конструируется из четырех не равнополочных уголков: сортамент стали по ГОСТ 8510-72, соответственно имеет две ветви, расстояние между которыми «а» (рассчитывается). Обе ветви сечения связаны между собой по вертикали вдоль стержня  соединительной решеткой (стальными планками) с шагом «b» (рассчитывается), соединение – на сварке. соединительной решеткой (стальными планками) с шагом «b» (рассчитывается), соединение – на сварке. Сплошное сечение конструируется прямоугольное сплошного сечения. Поперечное сечение горизонтальных стержней( траверс) из двух равнополочных уголков из сортамента прокатной стали по ГОСТ8509-72, имеет вертикальную плоскость симметрии, соединение на сварке. При изгибе таких стержней эпюра нормальных напряжений состоит из двух не равных треугольников. Условие задания
На рис. 1.1,а показана расчетная схема для вертикальной стержневой конструкции с нагрузками, приложенными в главной вертикальной плоскости инерции YZ. Мысленно можно считать, что вес гирлянд, проводов и троса – нагрузки 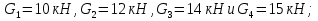 от ветра (перпендикулярно трассе воздушной линии) в пролете между опорами на проводов и трос – нагрузки от ветра (перпендикулярно трассе воздушной линии) в пролете между опорами на проводов и трос – нагрузки  Вертикальный стержень Вертикальный стержень  (ствол опоры) имеет длину (ствол опоры) имеет длину 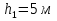 и форму из двух стальных швеллеров (рис. 1.1,б), соединение этих элементов рассчитывается (есть впереди). Номер швеллера и расстояние между ними «а» не знаем. и форму из двух стальных швеллеров (рис. 1.1,б), соединение этих элементов рассчитывается (есть впереди). Номер швеллера и расстояние между ними «а» не знаем.Рассчитываем реакции в опоре  из уравнений равновесия: суммы моментов относительно точки А (поперечной оси А), суммы проекций нагрузок на горизонтальную и вертикальную оси Y и Z имеем соответственно: из уравнений равновесия: суммы моментов относительно точки А (поперечной оси А), суммы проекций нагрузок на горизонтальную и вертикальную оси Y и Z имеем соответственно: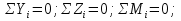 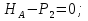 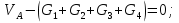   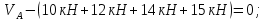 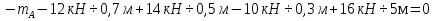 отсюда  Рассчитанные реакции показаны на рис. 1.1,а. На рис. 1.2 – расчетная схема для вертикального стержня АВ с приведенными нагрузками к верхнему краю от оголовка конструкции ( см. рис. 1,а): в точке В из уравнений равновесия имеем:   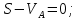 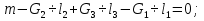 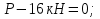  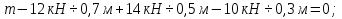 отсюда: 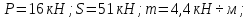 Значение P, S и m рассчитаны правильно, если реакция в опоре А (см. рис.1.2) такие же, как для стержневой конструкции на рис. 1.1,а (схемы статически эквивалентны). Стержень АВ высотой 5,0 м находится в условиях продольного поперечного изгиба. На рис. 1.3,а – стержень АВ в условия плоского поперечного изгиба от действия нагрузок P и m(S=0). Рассчитаем в произвольном сечении Z, как для консольной балки при поперечном изгибе: а) значения поперечной силы Q[кН]: 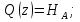 б) значения изгибающего момента М[  ]: ]: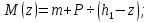 в) значение угла прогиба 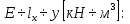 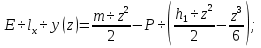 Результаты расчета заносим в таблицу Таблица 1.1
Из эпюры для изгибающего момента М(Z) видно (см. рис. 1.3,в), что опасным является сечение внизу стержня, где опора А при z=0 м, наибольшее значение (обозначаем его индексом буквой «о»): 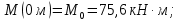 (1.0) (1.0)(ординаты показаны со стороны растянутых волокон). Знак минус «–» показывает, что в опасном сечении А при Z=0 м наиболее удаленные волокна от нейтрального слоя слева – растянуты, справа – сжаты. Наибольшее горизонтальное перемещение (прогиб) вверху стержня (см. рис.1.3,г) в точке В при Z=5 м (обозначаем его индексом буквой «о») 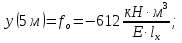 В этой формуле знак минус «–» показывает, что верхний край стержня при Z=5 м (точка В) под действием поперечных нагрузок (см. рис. 1.3,а) горизонтально перемещается вправо вдоль горизонтальной оси Y.
Стальной швеллер составного сечения (см. рис. 1.5) по ГОСТ 8240-97 (его номер пока не знаем). В нулевом приближении рекомендуется использовать условие прочности для поперечного изгиба  (как при растяжении, так и при сжатия момент сопротивления изгибу 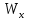 и основное допускаемое напряжение и основное допускаемое напряжение 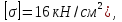 откуда откуда уголок не равнополочный № 20/12,5 12[1, по табл. на с. 613], для которого: 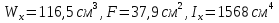 Подготавливаются числа для вычисления нормальных напряжений в первом приближении по формулам:  (1.1) (1.1)и 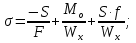 (1.2) (1.2)При этом используются 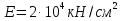 и и 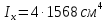 (так как составное сечение из четырех уголков) (так как составное сечение из четырех уголков)Наибольший прогиб при поперечном изгибе определяется по формуле: 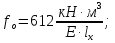  Эйлерова сила определяется по формуле:  (1.3) (1.3)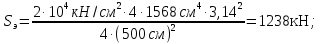 Наибольший прогиб при продольно-поперечном изгибе определяется по формуле:  (1.5) (1.5)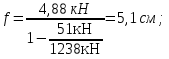 В первом приближении по формулам (1.1) и (1.2) с учетом результатов (1.3), (1.5) и значений 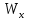 и F для уголка не равнополочного № 16/10 (в нулевом приближении) получается следующие нормальные напряжения в опасном сечении А: и F для уголка не равнополочного № 16/10 (в нулевом приближении) получается следующие нормальные напряжения в опасном сечении А:  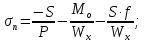 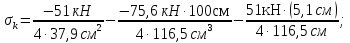 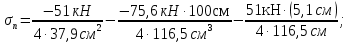 Где индексы «k» и «n» – соответственно обозначают наибольшее сжимающее напряжение в крайнем левом волокне и наибольшее растягивающее напряжение крайнем правом, как согласованы знаки в формулах: (1.1), (1.2) и (1.4). 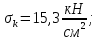 (а) (а) 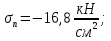 (б) (б)Результат (б) показывает, что крайнее правое волокно «n» сжато (а не растянуто) напряжением 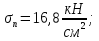 Оценим погрешность:  Эпюра для суммарных напряжений 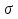 , рассчитанных по (а)…(б) изображена на рис. 1.4,б. , рассчитанных по (а)…(б) изображена на рис. 1.4,б.Перегруз 5% допустимо, так как не большее 5%(процентов). Окончательно выбираем уголок не равнополочных № 20/12,5 12 с перегрузом 5,0% по площади сечения ствола АВ. Эпюра для суммарных напряжений 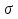 , рассчитанных по (а)…(б) изображена на рис. 1.4,б. , рассчитанных по (а)…(б) изображена на рис. 1.4,б.
Для гибкости 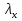 модно записать: модно записать:  Что допустимо, т.к. меньше предельной гибкости равной 180. Проверим выполнение условия устойчивости :  где  – допускаемое напряжение на устойчивость; – допускаемое напряжение на устойчивость; – коэффициент понижения основного допускаемого напряжения (0< – коэффициент понижения основного допускаемого напряжения (0< <1). <1).
С помощью таблицы и метода интерполяции получим : 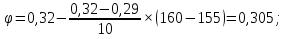 Напряжение в материале стержня от центрального сжатия: 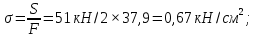 Допускаемое напряжение на устойчивость для материала стержня: 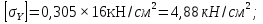 0,67<4,88 а значит 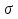 < <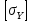 – условие устойчивости выполняется. – условие устойчивости выполняется.На рис.1.5,а – чертеж рассчитанного элемента вертикального стержня АВ – поперечное сечение из двух швеллеров.
Используем условие равноустойчивости: 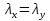 ; ;Откуда следует равенство осевых моментов инерции относительно главных центральных осей X и Y: 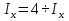   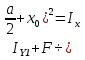   (1.8) (1.8)После приведений подобный слагаемых в (1.8), получается алгебраическое уравнение второй степени (квадратное)  откуда определим расстояние a:  (1.9) (1.9)Проверка. Подстановкой (1.9) в (1.8) имеем: 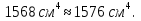 Погрешность обусловлена промежуточными округлениями при вычислениях на калькуляторе и составляет: 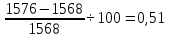 что допустимо. Определение вертикального расстояния «b» между соединительными планками. Расстояние «b» между двумя стальными пластинками (планками), которыми соединяются две ветви, определяется из условия:  где  – минимальный радиус инерции для одной ветви составного сечения стержня АВ. – минимальный радиус инерции для одной ветви составного сечения стержня АВ.С учетом значения 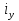 из (1.6) получаем: из (1.6) получаем: Конструктивно принимаем b=100см (рис.1.5,б). 2.Расчет на прочность сплошного ствола опоры 2.1 Расчет диаметров: внешнего – D и внутреннего – d, сплошного сечения ствола опоры Вертикальный стержень АВ имеет форму прямоугольника с размерами d и 2d (рис.1.2,в). Значение d пока неизвестно. Опасным является сечение внизу стержня при Z=0, где опора А (рис.1.3,а). предварительно рассчитываем (подготавливаем) числа для определения нормальных напряжений по формулам (6) и (7), при этом используем:  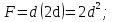   (2.2) (2.2)По формуле  наибольший прогиб при поперечном изгибе: наибольший прогиб при поперечном изгибе: Эйлерова сила: 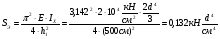 По формуле : набольший прогиб при продольно – поперечном изгибе: 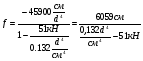 Нормальное напряжение в крайних левом (точка k) и правом (точка n) волокнах получаются по формулам (1.6) и (1.7) следующие нормальные напряжения в опасном сечении А:   Формула с учетом знака «-» показывает, что крайнее левое волокно « n » сжато (а не растянуто), здесь наибольшее сжимающее напряжение (подставим значения , и ): 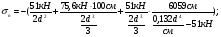 ; ; 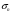 – наибольшее сжимающее напряжение от приложенных нагрузок, а допускаемое – для материала по условию , в итоге для вычисления имеем следующее нелинейное алгебраическое уравнение 7–й степени – наибольшее сжимающее напряжение от приложенных нагрузок, а допускаемое – для материала по условию , в итоге для вычисления имеем следующее нелинейное алгебраическое уравнение 7–й степени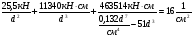 Здесь справа-первое слагаемое учитывает действие продольной нагрузки S; второе - поперечное нагрузки, влияние которой определяется изгибающим моментом ; третье – изгибающего момента , который создается нагрузкой . Приближенное значение (от поперечного изгиба ) можно подсчитать по формуле  , ,откуда  Проверка: , , 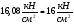 Подставляем значение d в (2.2) получим:  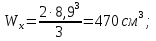 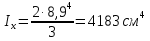 Подставим d в формулы для 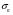 и и  получим: получим: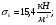  Условие прочности выполняется. 2.2 проверка стержня АВ на устойчивость. Для гибкости 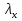 можно записать: можно записать: 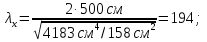 что не допустимо, так как превышает предельное значение гибкости, равное 180, тогда из условия: 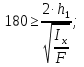  Определяем подходящее значение d [см]: 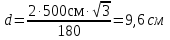 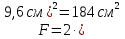 2.3 Сравнение веса сечения Если разделим вес составного стержня АВ на вес сплошного, то будем иметь отношения  Составной стержень АВ на 19% легче, чем сплошной. 3. Расчет траверсы из двух уголков 3.1Нахождение реакций в шарнирах и построение эпюр изгибающих моментов. На рис. 3.1,a стержневая конструкция статически неопределимая. Рассчитываем траверсу ВD приближенно с помощью схемы на рис. 3.1,б . В шарнире С одна реакция вдоль стержня и шарнире D одна, в шарнире В две реакции; горизонтальная и вертикальная. Реакции можно рассчитать с помощью уравнений реакции: 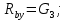  Рассчитанные реакции показаны на рис. 3.1,б. Определим значение внутренних изгибающих моментов М.   Из эпюры изгибающих моментов видно (рис. 3.1,в), что опасным является сечение траверсы в т. В. В точке В наиболее изгибающий момент. 3.2Выбор уголка Гибкость незначительна, так как траверса короткая (жесткая), поэтому в формулах (1.1) и (1.2) третьим слагаемым можно пренебречь. Наибольшее нормальное напряжение (сжимающее) в волокне «k» (рис. 3.2) 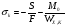 ; ; (3.1) (3.1)Где F и  площадь и момент сопротивления изгибу для одного уголка траверсы СВ. В нулевом приближении при поперечном изгибе площадь и момент сопротивления изгибу для одного уголка траверсы СВ. В нулевом приближении при поперечном изгибе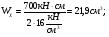 Принимаем: стальной равнополочный уголок № 11 110∙110∙8 ГОСТ 8503-72, для которого: 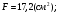  ; ;  В первом приближения по формуле (3.1) получается:  Оценим погрешность:  Что допустимо, так как не превышает 5%. Эпюры напряжений на рис.3.2. 3.2Проверка на устойчивость Для гибкости можно записать: 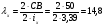 С помощью таблицы и интерполирования имеем следующие значения для коэффициента 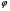
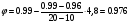 Напряжение в материале стержня от центрального сжатия:  Допускаемое напряжение на устойчивость для материала стержня: 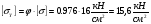 Устойчивость прямолинейной формы траверсы СВ надежная (обеспечена), так как напряжение 0,436 кН/  значительно меньше, чем допускаемое на устойчивость 15,6 кН/ значительно меньше, чем допускаемое на устойчивость 15,6 кН/ для материала. для материала.Заключение В данной курсовой работе для имеющейся схемы опоры выполнены следующие расчеты: подобрали (рассчитали) по варианту составное сечение ствола СВ опоры из проката по таблицам сортамента; определили расстояние «а» между ветвями составного сечения ствола СВ; определили расстояние «в» между планками соединительной решетки ствола СВ; рассчитали размеры поперечного сечения сплошного стального ствола СВ; сравнили вес (в процентах) составного вертикального стержня СВ и сплошного. Для сплошного ствола опоры, который имеет форму прямоугольного сечения, определено расстояние 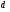 . Также был подобран номер профиля для траверсы опоры, состоящий из двух стальных равнополочных уголков. . Также был подобран номер профиля для траверсы опоры, состоящий из двух стальных равнополочных уголков.Использовали персональную ЭВМ (ПЭВМ) и программу pd6b. pas. Список литературы
Приложение Файл решения (программа pd6b1.pas) вариант: 8 вы ввели следующие значения: номер схемы опоры (формы сечения) R=2 длина (высота) ствола опоры L= 5.000 м приложенная нагрузка сверху вниз S= 51.000 кН изгибающий момент (внутренний) M0= -75.600 кН*м прогиб (горизонтальный) при поперечном изгибе, умноженный на жесткость при изгибе, f0= -612.000 кН*м*м*м модуль упругости при растяжении E= 20000.000 кН/(см*см) результаты вычислений: при поперечном изгибе размер сечения d (для кольца - наружный диаметр) d= 8.916 см F= 158.986 см*см WX= 472.500 см*см*см IX= 4212.755 см*см*см*см SK= 16.0000 кН/(см*см) (слева) SN= -16.0000 кН/(см*см) (справа) f0= -7.264 см при продольно-поперечном изгибе эйлерова сила Sa= 907.928 кН S/Sa= 0.056 прогиб (горизонтальный) f= -7.049 см размер сечения d (для кольца - наружный диаметр) d= 9.115 см j=200- количество итераций F= 166.162 см*см WX= 504.850 см*см*см IX= 4601.645 см*см*см*см (SF1= 0.30700 M0WX= -14.980 SffWX= -0.712) нормальные напряжения в опасном сечении: SK= 15.385 кН/(см*см) (слева) SN= -15.999 кН/(см*см) (справа) (для справки: при поперечном изгибе f0= -6.653 см) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 я
я


