курсовой проект пути сообщения. курсовой проект, пути сообщения Каргин А.А.2к.3г.ЭЖД,заочное.. Курсовой проект по дисциплине Пути сообщения Каргин А. А. студент 2 курса эжд,3группы,заочного отделения Зачетная книжка 242

• Название: Курсовой проект по дисциплине Пути сообщения Каргин А. А. студент 2 курса эжд,3группы,заочного отделения Зачетная книжка 242
• Анкор: курсовой проект пути сообщения
• Дата: 20.04.2021
• Размер: 1.52 Mb.
• Имя файла: курсовой проект, пути сообщения Каргин А.А.2к.3г.ЭЖД,заочное..docx
• Тип: Курсовой проект; #196795
• страница: 3 из 3

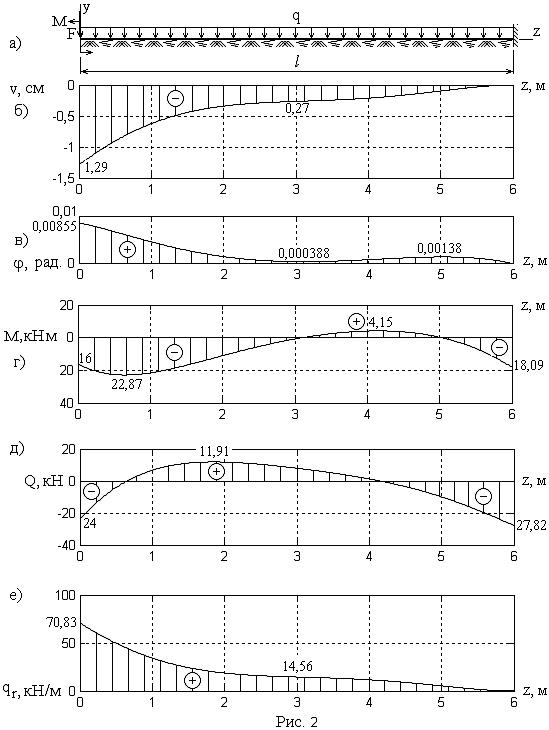
Расчетные схемы рельс

1

2

3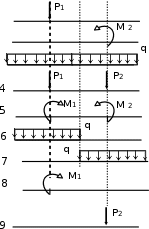
Схемы нагрузок

1

2

3

3.2 Статический расчёт рельса на прочность

Рельс рассматривается как неразрезная балка, лежащая на сплошном упругом основании

Для рельса, расположеннго на упругом основании, при модуле упругости равном E= 210 ГПа требуется:

1.Записать с помощью метода начальных параметров выражения для прогибов v, углов поворота поперечных сечений и, изгибающих моментов Mи поперечных сил Qна всех участках балки.

2.Поставить граничные условия и определить неизвестные начальные параметры.

3.Провести расчеты на компьютере и построить эпюры Q, M,   , v.

4.Построить эпюру реактивного отпора основания.

5.Определить реакции опор, если они имеются.

6.Проверить прочность балки, приняв коэффициент надежности по нагрузке   , расчетное сопротивление R= 210 МПа и коэффициент условий работы   .

 Расчётная схемаАналитическое решение

 Для балки в виде стального прокатного двутавра №22 выпишем осевой момент инерции J = J_x = 2550 см⁴ и ширину полки с = 11 см. Обозначим и определим жёсткость балки

 Нм   .

Для упрощения дальнейших вычислений введём обозначения безразмерной переменной 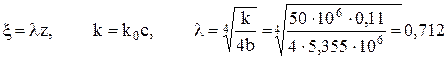  , коэффициента постели k и затем вычислим параметр 

 1/м.

Запишем с помощью метода начальных параметров выражение для прогиба балки в произвольном сечении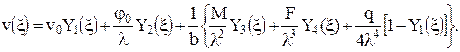

 (1)

Здесь v₀, 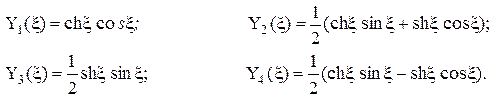  - начальные параметры, представляющие собой прогиб и угол поворота в начале координат, т. е. на левом конце балки z = 0   . Y₁, Y₂, Y₃, Y₄ – функции А.Н.Крылова, которые определяются из специальных таблиц или по формулам:

 (2)

Эти функции обладают свойством повторяемости при дифференцировании

 (3)

Пользуясь формулой (1) и далее вытекающими из неё выражениями для характеристик балки, следует помнить, что нагрузки M, F, q имеют знаки, установленные для них в методе начальных параметров и зависящие от их направлений. В частности, в данной задаче эти знаки будут отрицательными.

Неизвестные начальные параметры определим из граничных условий на правом конце балки:

 (4)

Смысл уравнений (4) в том, что прогиб и угол поворота правого концевого сечения должны равняться нулю вследствие его заделки.

Запишем выражения для углов поворота поперечных сечений, изгибающих моментов и поперечных сил.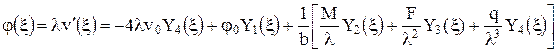

 . (5)

 (6)

 (7)

Вычисляем аргументы и значения функций А.Н.Крылова для выполнения граничных условий (4)

 ,   ,

 ,   ,   .

Раскроем граничные условия (4) с помощью формул (1) - (3). При этом единицы измерения силовых величин для удобства вычислений переведём в килоньютоны.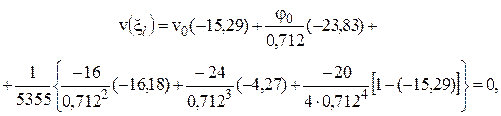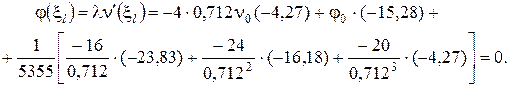





После элементарных упрощений получена система двух алгебраических уравнений относительно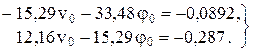 



Решая, имеем

 см,   рад.


Далее расчёты производим с помощью компьютерной программы кафедры теоретической и прикладной механики. Полученные эпюры   приведены на рис. 2. Числа, подписанные для характерных точек, взяты визуально с экрана монитора при многократных увеличениях графиков и обладают высокой степенью точности.

Реакции в правой опоре можно определить по эпюрам изгибающих моментов 2в и поперечных сил 2г или по обращению к компьютеру с запросом. Получено, что они имеют значения

M_l =18,09 кНм, направлен по часовой стрелке,

R_l = 27,82 кН, направлена вверх.

Ординаты реактивного отпора основания определяем по формуле Винклера

 .

Здесь знак минус учитывает, что   имеют противоположные направления. Результаты счёта на компьютере показаны на рис. 2е. Равнодействующая этой реакции, вычисленная как определённый интеграл методом трапеций, составляет

R = 116,79 кН.

Проверим равновесие балки.



Относительная погрешность составляет

 .

Очевидно, что равновесие обеспечено. Вычисления правильны.

Расчётное значение наибольшего изгибающего момента равно:



Выполняем проверку условия прочности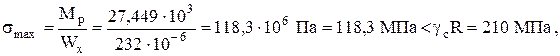



где   см   - момент сопротивления двутавра №22.

Условие прочности выполняется. Прочность обеспечена.

Решение методом конечных разностей

Изогнутая ось балки описывается обыкновенным дифференциальным уравнением четвёртого порядка

 , (8)

k – коэффициент постели, знак минус в правой части соответствует нагрузке, направленной вниз. Разделим уравнение на   , обозначим

 .

и получим вместо (8)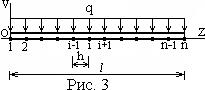

 . (9)

 Область непрерывного изменения аргумента   заменим областью дискретного изменения аргумента –сеткой (рис. 3)

 .

Множество точек с номерами   называется сеткой, а сами точки - узлами сетки. Вместо функции непрерывного аргумента   будет отыскиваться сеточная функция   .

К уравнению (6) присоединяются граничные условия. На левом конце балки изгибающий момент и поперечная сила в сечении равны приложенным нагрузкам

 . (10)

На правом конце балки - заделка. Поэтому прогиб и угол поворота сечения равны нулю

 . (11)


Пользуясь пятиточечным шаблоном сетки (рис. 4),

заменим производные в задаче (6) – (8) конечноразностными соотношениями: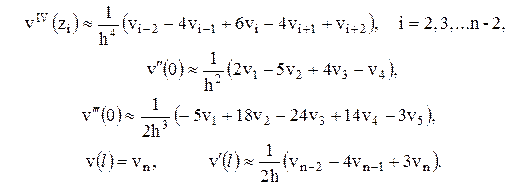

 (12)

Подстановка (12) в задачу (9) – (11) и несложные преобразования приводят к системе алгебраических уравнений относительно вектора 

 , (13)

гд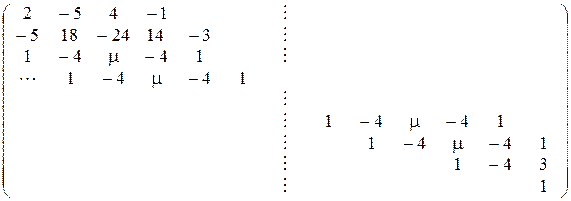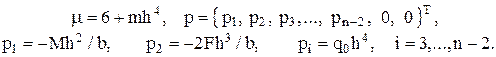е

A =   ,



Нулевые элементы матрицы не показаны, значок   в индексе соответствует операции транспонирования.

Система уравнений (13) решается на компьютере с помощью подпрограммы пакета математических программ MATLAB, в результате чего становится известным вектор v.

Далее с помощью конечноразностных замен производных вычисляются угол поворота и внутренние силы в сечениях по формулам

 .

Реактивный отпор основания определяем, как и в предыдущем варианте решения, с помощью формулы Винклера

 .

Результаты счёта почти точно совпадают с данными эпюр, изображённых на рис. 2.

Заключение

В процессе выполнения курсового проекта приобретены следующие навыки:

• 
  в зависимости от грузонапряженности и скоростей движения поездов выбирать и назначать группу, категорию и класс пути;
  
• 
  выбирать конструкцию верхнего строения пути;
  
• 
  Разрабатывать типовые нормальные поперечные профили насыпи и выемки.
  
• 
  Расчитывать железнодорожный путь на прочность
  

Данная курсовая работа состоит из пояснительной записк, списка литературы и приложения.

Список использованной литературы

Железнодорожный путь: Учебник / Ашпиз Е.С., Гасанов А.И., Глюзберг

Б.Э.; Под ред. Ашпиз Е.С. - Москва :УМЦ ЖДТ, 2014. - 544 с.: 60x84 1/16. - (Высшее профессиональное образование) (Переплёт) ISBN 978-5-89035-689-5

Методические указания к выполнению практических работ по дисциплине пути сообщения для студентов специальности 23.05.04 «Эксплуатация железных дорог» очной и заочной форм обучения . Эрлих. (4306)

Н. С. Черняева Верхнее строение пути: учеб. ил. пособие для студ. техн., колледжей и для проф. подг. работн. ж.-д. трансп. М.: УМЦ по образов. на ж.-д. трансп., 2008

Приложение

1.Поперечный профиль насыпи.

2.Поперечный профиль выемки

3.Поперечный профиль основной площадки земляного полотна на раздельном пункте.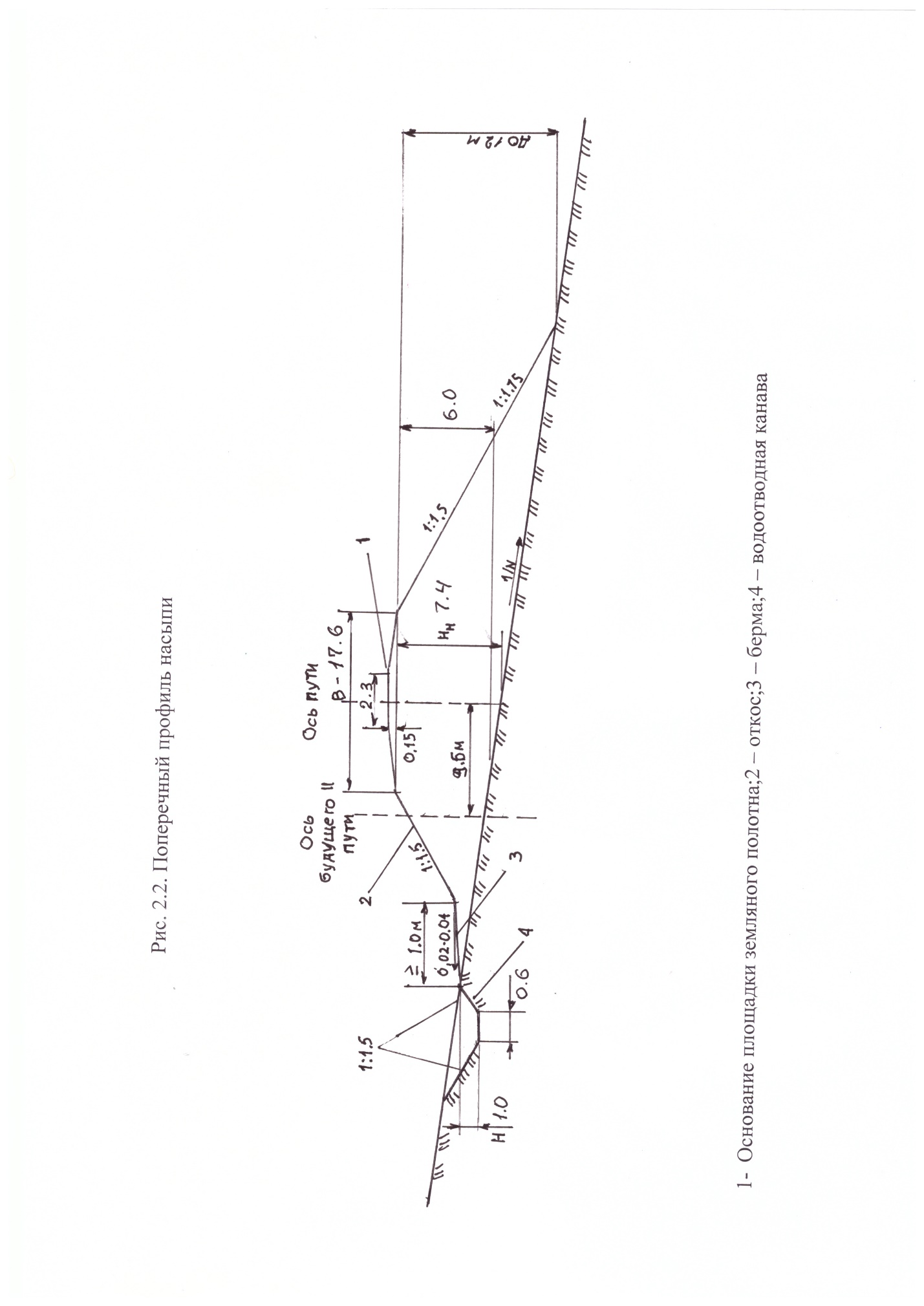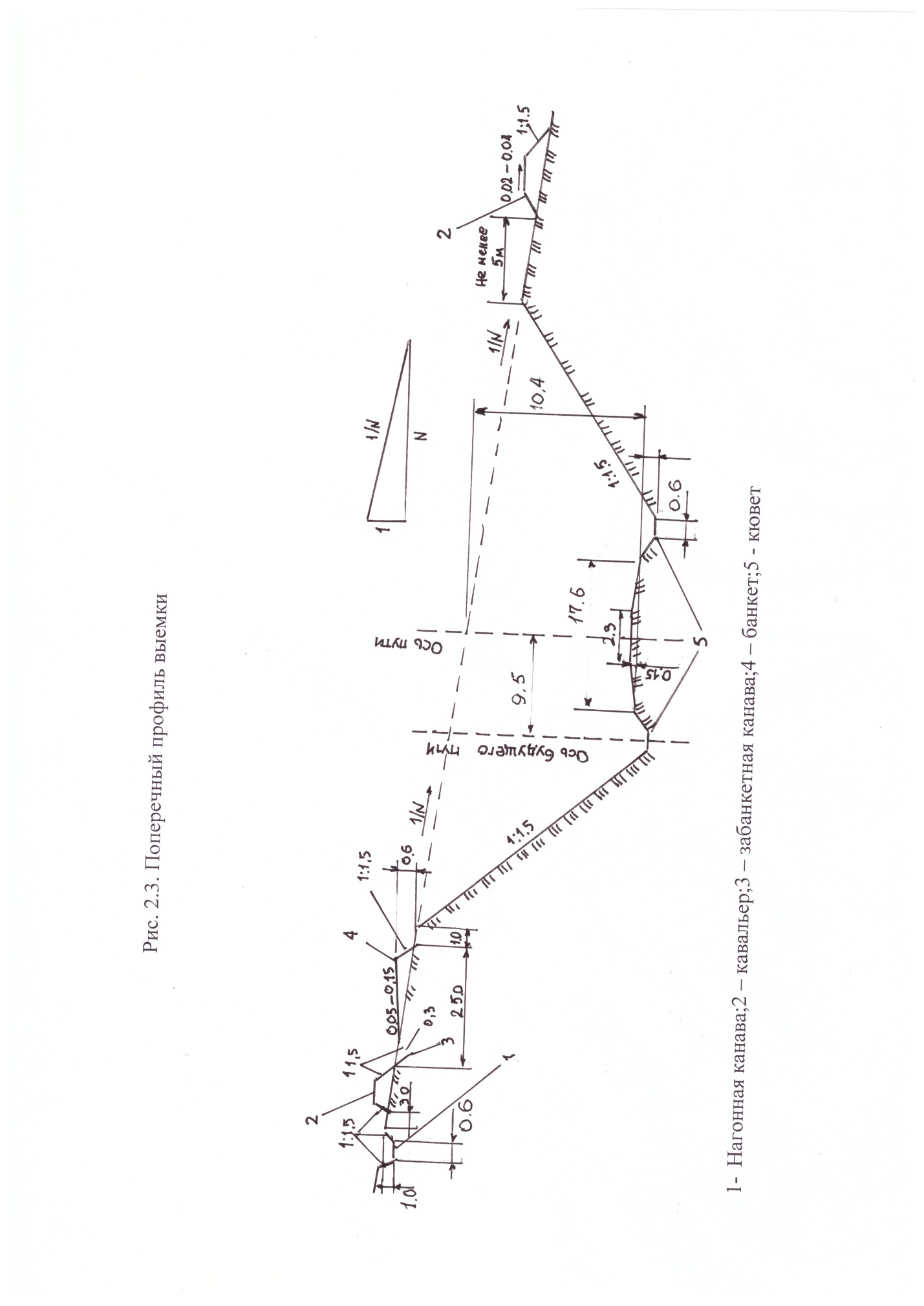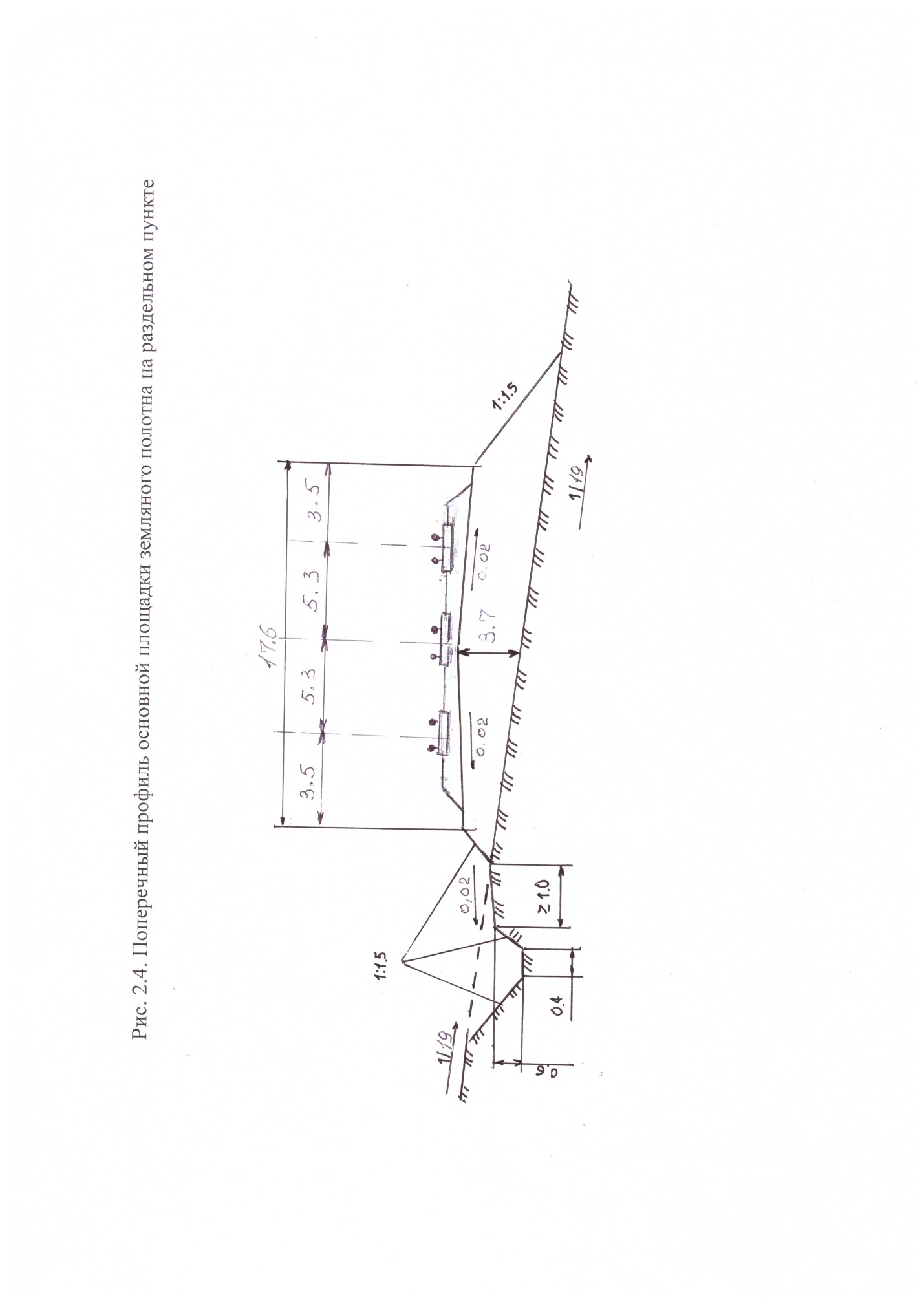