7 варик. Курсовой проект по дисциплине Теория информации. Системы сбора, обработки и передачи информации На тему Расчётная часть проекта телемеханической компьютеризованной системы сбора, обработки и передачи информации
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
5.3 Верификация кодовой посылки (на примере команды ТУ). Деление кода передаваемой команды ТУ без остатка на двоичный эквивалент образующего полинома означает, что в коде отсутствуют одно-, двух- и трёхкратные ошибки. Осуществляется путём деление кода передаваемой команды на двоичный эквивалент образующего полинома
6.1.Количество информации в потоке сообщений. Потоком событий источника сообщений называется последовательность во времени его состояний. Каждое состояние источника представлено соответствующим символом в сообщении. Поток событий бинарного источника сообщений может быть представлен последовательностью, составленной из единиц и нулей. Рассмотрим такую последовательность как сообщение длиной в 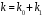 символов, включающее символов, включающее 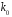 нулей и нулей и 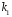 единиц. При заданных величинах единиц. При заданных величинах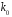 и и 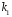 количество таких сообщений количество таких сообщений 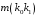 определяется всеми возможными сочетаниями определяется всеми возможными сочетаниями 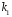 =6 единиц и =6 единиц и 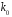 =16 нулей из =16 нулей из 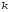 =22 символов 1001 1000 0100 0000 010100 =22 символов 1001 1000 0100 0000 010100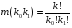 . (6.1) . (6.1)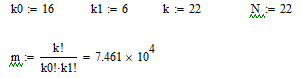 Конкретное сообщение, содержащее 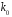 нулей и нулей и 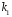 единиц, представляет собой одно такое сочетание. С его приходом снимается предшествовавшая ему неопределённость. Вместо единиц, представляет собой одно такое сочетание. С его приходом снимается предшествовавшая ему неопределённость. Вместо 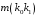 возможных сообщений имеем одно конкретное. возможных сообщений имеем одно конкретное. Количество информации в сообщении является мерой этой неопределённости и пропорционально логарифму 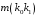 . . 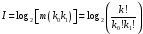 . (6.2) . (6.2)Энтропия 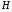 источника сообщений представляет собой количество информации, приходящееся в среднем на один символ. источника сообщений представляет собой количество информации, приходящееся в среднем на один символ. 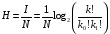 . (6.3) . (6.3)H = 0.763 Если символы генерируются источником равномерно во времени с частотой (интенсивностью) 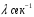 , то энтропия указывает скорость производства информации. , то энтропия указывает скорость производства информации.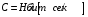 . (6.4) . (6.4)Для нормальной работы телемеханического канала его пропускная способность должна быть не меньше максимальной скорости производства информации. При логарифмировании иногда удобно выразить логарифм по основанию два через натуральный или десятичный логарифм. Для этого можно воспользоваться формулой пересчёта 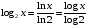 (6.5) (6.5)6.1.1 Максимальная средняя энтропия источника команд ТУ
Код КНБ представляет собой уникальную комбинацию 01111110, которая не может встретиться в иных частях пакета. Это обеспечивается стаффингом – добавлением после каждых пяти «1» в коде сообщения нуля и удалением этих нулей на стороне приёма перед декодированием. В проектируемом канале ТУ стаффинг не требуется, так как байты не могут содержать код, аналогичный КНБ. В то же время, в каналах ТС и ТУ стаффинг является обязательным. Для каждой строки n=1,…,18 таблицы кодов ТУ определяем количество единиц 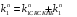 и нулей и нулей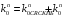 в блоке. Вычисляем отношение в блоке. Вычисляем отношение 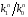 . Выбираем строку (строки) для которых это отношение минимально отличается от единицы. Для выбранной строки (строк) вычисляем энтропию по формуле (6.3). . Выбираем строку (строки) для которых это отношение минимально отличается от единицы. Для выбранной строки (строк) вычисляем энтропию по формуле (6.3).Пусть, например, такой строкой является первая строка таблицы кодов ТУ. Для неё имеем 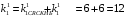 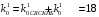 Количество информации в сообщении первой строки кодов ТУ 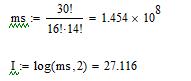 I = 27.116 бит Таким образом, при заданном распределении единиц и нулей в сообщении длиной 30 бинарных символов содержится в среднем 27,116 бит информации. Средняя энтропия сообщения в канале ТУ 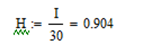 НTY = 0.904 бит/символ 6.1.2 Максимальная средняя энтропия источников ТС и ТИ Таблица максимальных кодов ТС
Таблица максимальных кодов ТИ
Здесь максимальная средняя энтропия 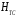 и и 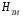 вычисляется по таблицам максимальных кодов ТС и ТИ. Процедура вычислений аналогична представленной выше. вычисляется по таблицам максимальных кодов ТС и ТИ. Процедура вычислений аналогична представленной выше.Максимальная средняя энтропия 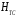 : :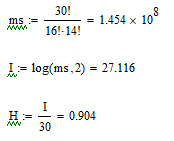 Максимальная средняя энтропия 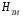 : :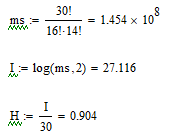
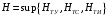 = 0.904 бит/символ (6.6) = 0.904 бит/символ (6.6)
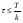 , , 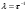 (6.7) (6.7)где 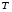 - наибольшее допустимое время передачи блока данных в каналах ТУ, ТС и ТИ - наибольшее допустимое время передачи блока данных в каналах ТУ, ТС и ТИ 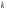 - количество элементарных сигналов (символов) в блоке сообщений (длина блока). В нашем случае - количество элементарных сигналов (символов) в блоке сообщений (длина блока). В нашем случае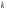 =30. Получим =30. ПолучимT = 875 мкс 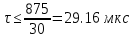 . .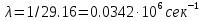 6.3. Полоса частот канала связи 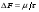 , (6.8) , (6.8)где 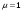 - коэффициент формы для видеоимпульса, - коэффициент формы для видеоимпульса, 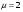 - коэффициент формы для радиоимпульса в случае амплитудной, частотной или фазовой манипуляции. - коэффициент формы для радиоимпульса в случае амплитудной, частотной или фазовой манипуляции.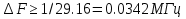 Принимаем 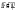 34кГц 34кГц6.4 Требуемая скорость передачи информации. 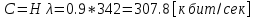 . . |

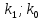
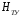 ,
,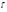 и интенсивность
и интенсивность