«ОБРАБОТКА РЕЗУЛЬТАТОВ НЕСКОЛЬКИХ СЕРИЙ ИЗМЕРЕНИЙ». КП ПРОКИНА АННА 620591. Курсовой проект по теме обработка результатов нескольких серий измерений
 Скачать 200.02 Kb. Скачать 200.02 Kb.
|
Министерство образования и Науки РоссииФГБОУ ВО ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТКУРСОВОЙ ПРОЕКТ по теме: «ОБРАБОТКА РЕЗУЛЬТАТОВ НЕСКОЛЬКИХ СЕРИЙ ИЗМЕРЕНИЙ» Вариант № 13
Тула, 2020Содержание Подготовка результатов наблюдений в отдельных сериях измерений к совместной обработке………………………………………………………. 4 Расчет числовых характеристик законов распределения вероятности (ЗРВ) результатов измерения (РИ)………………………………………4 Первая серия………………………………………………………………5 Вторая серия………………………………………………………………5 Третья серия………………………………………………………………5 Исключение промахов……………………………………………………6 Проверка гипотезы об однородности результатов серий измерений……8 Проверка гипотезы о совпадения средних арифметических значений результатов наблюдений в сериях………………………………………8 Проверяем первую пару средних: 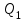 и и 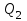 ……………………………9 ……………………………9Проверяем первую пару средних: 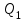 и и 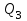 ……………………………10 ……………………………10Проверяем первую пару средних: 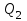 и и 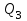 ……………………………11 ……………………………11Проверка гипотезы об однородности дисперсий серий измерений (равноточности или равнорассеяности результатов серий) …………13 Проверяем однородность наибольшей и наименьшей дисперсий …14 Обработка результатов неравноточных серий измерений……………….15 Расчет оценки среднего значения 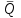 измеряемой физической величины………………………………………………………………….16 измеряемой физической величины………………………………………………………………….16Расчет оценки СКО 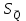 среднего взвешенного значения среднего взвешенного значения 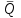 измеряемой физической величины…………………………………………………….17 измеряемой физической величины…………………………………………………….17Запись результата измерения в принятом виде…………………………18 Список литературы…………………………………………………………..19 Дисциплина — Метрология, стандартизация и сертификация Часть I — Обработка результатов нескольких серий измерений Группа № 620591, номер по журналу — 13, студент — __Прокина Анна Сергеевна___ Шифр задания 620591 0 G 0 .16 44.9 Результаты первой серии измерений 45.02 44.99 44.89 44.98 44.94 45.05 45.15 44.85 45.03 44.84 45.07 44.75 44.85 45.04 45.14 Результаты второй серии измерений 45.03 45.01 44.94 44.85 44.81 44.43 44.84 44.84 45.06 44.90 44.41 45.26 44.59 44.85 44.72 Результаты третьей серии измерений 44.97 44.90 44.67 45.58 45.01 45.26 44.87 44.74 45.10 45.13 44.76 44.85 44.47 Записать результат с доверительной вероятностью P = 0.91 1. ПОДГОТОВКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ В ОТДЕЛЬНЫХ СЕРИЯХ ИЗМЕРЕНИЙ К СОВМЕСТНОЙ ОБРАБОТКЕ Расчет числовых характеристик законов распределения вероятности (ЗРВ) результатов измерения (РИ) Даны три серии измерений. Для каждой серии необходимо найти среднее арифметическое значение, среднее квадратическое отклонение (в дальнейшем СКО) и среднее квадратическое отклонение среднего арифметического. Среднее арифметическое находим по формуле: 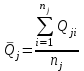 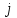 - порядковый номер серии измерений, - порядковый номер серии измерений,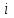 - порядковый номер измерения (наблюдения) в серии, - порядковый номер измерения (наблюдения) в серии,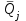 -среднее арифметическое (СА) результатов наблюдений в j-й серии, -среднее арифметическое (СА) результатов наблюдений в j-й серии,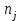 -число измерений в j-й серии. -число измерений в j-й серии.СКО находим по формуле: 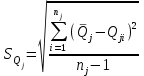 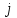 - порядковый номер серии измерений, - порядковый номер серии измерений,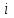 - порядковый номер измерения (наблюдения) в серии, - порядковый номер измерения (наблюдения) в серии,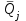 -среднее арифметическое (СА) результатов наблюдений в j-й серии, -среднее арифметическое (СА) результатов наблюдений в j-й серии,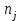 -число измерений в j-й серии, -число измерений в j-й серии,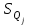 - оценка среднего квадратического отклонения (СКО) результатов - оценка среднего квадратического отклонения (СКО) результатовнаблюдений в j-й серии. СКО среднего арифметического находим по формуле: 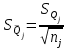 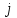 - порядковый номер серии измерений, - порядковый номер серии измерений,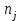 -число измерений в j-й серии, -число измерений в j-й серии,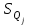 - оценка среднего квадратического отклонения (СКО) результатов - оценка среднего квадратического отклонения (СКО) результатовнаблюдений в j-й серии. 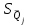 -оценка СКО СА результатов наблюдений в j-й серии. -оценка СКО СА результатов наблюдений в j-й серии.Первая серия. Среднее арифметическое первой серии: 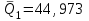 Среднее квадратическое отклонение первой серии: 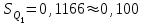 Среднее квадратическое отклонение среднего арифметического первой серии: 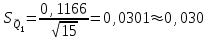 Вторая серия. Среднее арифметическое второй серии: 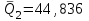 Среднее квадратическое отклонение второй серии: 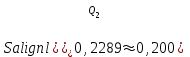 Среднее квадратическое отклонение среднего арифметического второй серии: 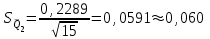 Третья серия. Среднее арифметическое третий серии: 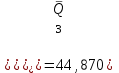 Среднее квадратическое отклонение третий серии: 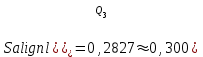 Среднее квадратическое отклонение среднего арифметического третий серии: 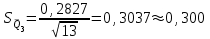 Исключение промахов Исключение промахов проводится так же, как при обработке результатов прямых равноточных многократных измерений. При незамеченном нарушении условий опыта или ошибки экспериментатора при снятии показаний с прибора и т.д. могут возникнуть грубые ошибки (промахи) или, как их еще называют, резко выделяющиеся наблюдения. Такие наблюдения следует исключить из результатов измерений. Отличить грубые промахи от случайных разбросов можно с помощью r-критерия: 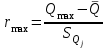 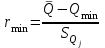 Расчетные 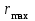 и и 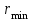 сравниваются с табличным значением r-критерия. сравниваются с табличным значением r-критерия. Результат опыта считается грубым промахом, если: 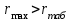 или или 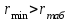 Допускаемые значения r-критерия зависят от числа степеней свободы f и уровня значимости α = 1 - P. Число степеней свободы определяется как: 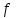 = n – 2 = n – 2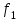 = 15 − 2 = 13 = 15 − 2 = 13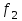 = 15 − 2 = 13 = 15 − 2 = 13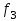 = 13− 2 = 11 = 13− 2 = 11Закон распределения нормальный, поэтому доверительная вероятность: P =0,95 тогда уровень значимости для всех серий будет равен: α = 1 - 0,95=0,05 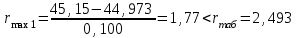 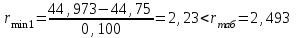 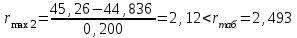 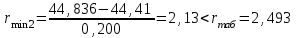 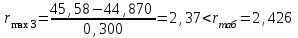 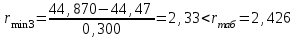 Условия выполняются значит в данной серии измерений грубых промахов нет. ПРОВЕРКА ГИПОТЕЗЫ ОБ ОДНОРОДНОСТИ РЕЗУЛЬТАТОВ СЕРИЙ ИЗМЕРЕНИЙ. Проверка гипотезы о совпадения средних арифметических значений результатов наблюдений в сериях Проверка гипотезы проводится попарно для всех возможных сочетаний пар серий. Ее идея заключается в следующем. Если модуль разности сравниваемых СА результатов наблюдений в сериях оказывается меньше, чем случайная погрешность, с которой эту разность можно определить, то расхождение СА результатов наблюдений в сериях признается случайным, а сами средние значения совпадающими с принятой доверительной вероятностью Р. Формально эта проверка сводится к проверке выполнения условия: 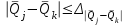 k — порядковый номер одной из сравниваемых серий измерений, j ≠ k, 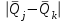 — модуль разности СА сравниваемых серий, — модуль разности СА сравниваемых серий,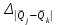 — случайная погрешность модуля разности СА сравниваемых серий, — случайная погрешность модуля разности СА сравниваемых серий,Данную проверку необходимо выполнить для всех возможных парных сочетаний серий измерений. Т.е. для наших трех серий проверяем следующие пары средних: 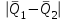 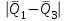 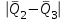 Оценка СКО модуля разности СА результатов наблюдений в сравниваемых сериях определяется по формуле: 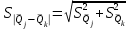 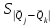 — оценка СКО модуля разности СА результатов наблюдений в сравниваемых сериях. — оценка СКО модуля разности СА результатов наблюдений в сравниваемых сериях.k — порядковый номер одной из сравниваемых серий измерений, j ≠ k. Учитывая нормальность распределения погрешности ∆, запишем ее значение в следующем виде: 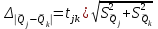 k — порядковый номер одной из сравниваемых серий измерений, j ≠ k, 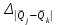 — случайная погрешность модуля разности СА сравниваемых серий, — случайная погрешность модуля разности СА сравниваемых серий,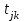 — относительная величина доверительного интервала случайной погрешности модуля разности СА сравниваемых серий — относительная величина доверительного интервала случайной погрешности модуля разности СА сравниваемых серийВ формуле неизвестной осталась величина 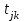 – относительная ширина доверительного интервала. – относительная ширина доверительного интервала.Число степеней свободы 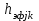 определяется по формуле: определяется по формуле: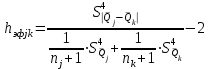 Так как числа степеней свободы h в таблицах, описывающих закон распределения Стьюдента, задаются целыми числами, приходится t определять, используя линейную интерполяцию, по одной из формул: 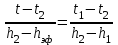 Проверяем первую пару средних: 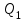 и и 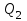 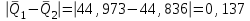 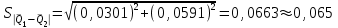 Находим 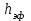 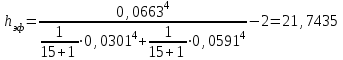 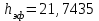 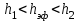 , то есть , то есть 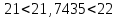 При заданной доверительной вероятности по таблице распределения Стьюдента находим: 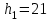 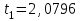 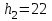 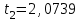 Определяем ширину доверительного интервала 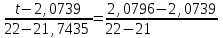 Отсюда 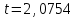 Вычисляем погрешность разности средних 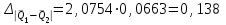 Проверяем условие 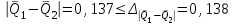 Условие выполняется, делаем вывод о совпадении средних значений первой и второй серий Проверяем вторую пару средних: 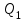 и и 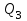 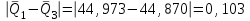 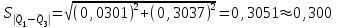 Находим 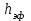 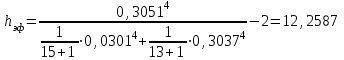 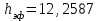 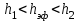 , то есть , то есть 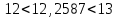 При заданной доверительной вероятности по таблице распределения Стьюдента находим: 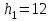 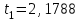 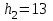 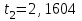 Определяем ширину доверительного интервала 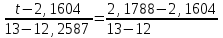 Отсюда 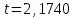 Вычисляем погрешность разности средних 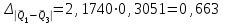 Проверяем условие 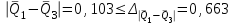 Условие выполняется, делаем вывод о совпадении средних значений первой и третьей серий Проверяем третью пару средних: 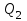 и и 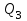 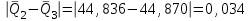 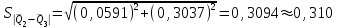 Находим 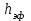 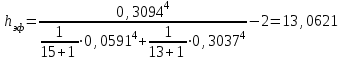 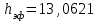 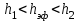 , то есть , то есть 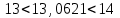 При заданной доверительной вероятности по таблице распределения Стьюдента находим: 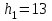 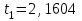 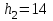 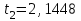 Определяем ширину доверительного интервала 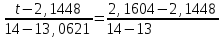 Отсюда 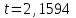 Вычисляем погрешность разности средних 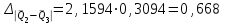 Проверяем условие 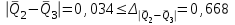 Условие выполняется, делаем вывод о совпадении средних значений второй и третьей серий Проверка гипотезы об однородности дисперсий серий измерений (равноточности или равнорассеянности результатов серий) Проверку совпадений дисперсий чаще всего проводят с использованием двух статистических критериев: 1. G-критерия Кохрэна; 2. F-критерия Фишера. Необходимым условием для использования критерия Кохрэна является то, что число измерений во всех сериях должно быть одинаковым. Это условие не соблюдается, поэтому будем использовать критерий Фишера. Проверка однородности дисперсий по критерию Фишера осуществляется следующим образом. Рассчитывается значение критерия Фишера по формуле: 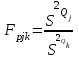 при 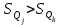 . Т.к. значение критерия Фишера всегда больше 1, поэтому в числителе должна находиться наибольшая из двух сравниваемых дисперсий. . Т.к. значение критерия Фишера всегда больше 1, поэтому в числителе должна находиться наибольшая из двух сравниваемых дисперсий.Как видно из формулы, критерий Фишера подразумевает попарное сравнение дисперсий. Поэтому, если серий больше двух, необходимо рассчитывать значение дисперсий. Поэтому, если серий больше двух, необходимо рассчитывать значение критерия Фишера для всех возможных парных сочетаний дисперсий. Две дисперсии считаются однородными, если выполняется следующее условие: 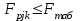 Критическое значение F-критерия выбирается по таблицам, исходя из значения доверительной вероятности P и чисел степеней свободы в сериях, которые определяются как: 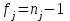 или или 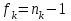 Проверяем однородность наибольшей и наименьшей дисперсий 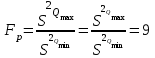 Определяем число степеней свободы первой и третьей серий измерений 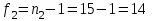 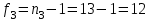 Из таблицы находим 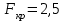 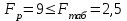 Условие не соблюдается, значит, максимальные и минимальные дисперсии не совпадают между собой, значит, серии признаются не равноточными. ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ СЕРИЙ ИЗМЕРЕНИЙ Неравноточные измерения вместе объединять нельзя, поэтому схема обработки результатов несколько иная. Среднее значение из нескольких серии измерений определяется, как среднее взвешенное: 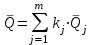 Где m — количество серий измерений; 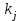 — j-й весовой коэффициент, учитывающий метрологическую ценность результата j-й серии. — j-й весовой коэффициент, учитывающий метрологическую ценность результата j-й серии.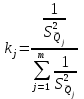 Сумма всех коэффициентов равна 1 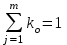 Для проверки правильности за счетом среднего взвешенного полезно использовать неравенство: 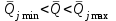 Оценка среднего квадратического 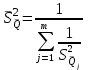 Доверительный интервал записывается в обычной форме 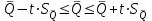 где t –ширина доверительного интервала Если число прямых измерений невелико, то параметр t выбирают по таблице распределения Стьюдента в зависимости от прямого уровня доверительной вероятности P и эффективного числа степеней свободы 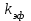 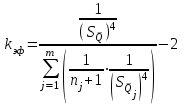 Так как числа степеней свободы k в таблицах, описывающих закон распределения Стьюдента, задаются целыми числами, приходится t определять, используя линейную интерполяцию, по одной из формул: 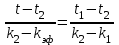 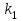 и и 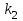 -числа степеней свободы, между которыми находятся значение -числа степеней свободы, между которыми находятся значение 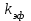 Расчет оценки среднего значения 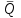 измеряемой физической величины измеряемой физической величины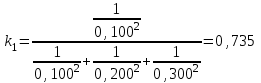 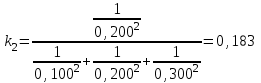 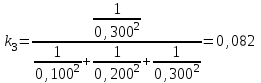 Проверяем сумму коэффициентов: 0,735+0,183+0,082=1,000 Решения верны Среднее взвешенное: 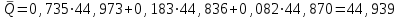 Имеем: 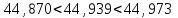 Расчет оценки СКО 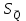 среднего взвешенного значения среднего взвешенного значения 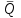 измеряемой физической величины 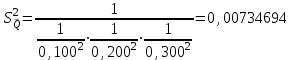 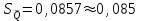 Находим 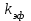 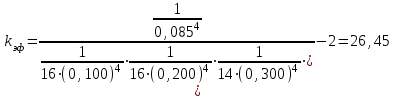 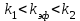 , то есть , то есть 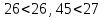 При заданной доверительной вероятности по таблице распределения Стьюдента находим: 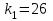 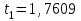 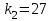 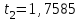 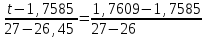 Отсюда 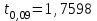 Запись результата измерения в принятом виде Записываем доверительный интервал в форме 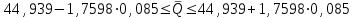 Окончательный результат: 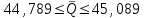 Список литературы Соловьев С. И. Методические указания по выполнению курсового проекта по дисциплине «Метрология» |
