курсовая работа. курсовой ТОЕ. Курсовой тое для электрической цепи, соответствующей номеру варианта и изображённой на рисунке 1, выполнить следующее
 Скачать 150.18 Kb. Скачать 150.18 Kb.
|
Курсовой ТОЕДля электрической цепи, соответствующей номеру варианта и изображённой на рисунке 1, выполнить следующее:Составить на основании законов Кирхгофа систему уравнений для расчёта токов во всех ветвях схемы. Определить токи во всех ветвях схемы методом контурных токов. Определить токи во всех ветвях схемы методом узловых потенциалов. Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить их между собой. Составить баланс мощностей в исходной схеме (схеме с источником тока), вычислив отдельно суммарную мощность источников и суммарную мощность нагрузок (сопротивлений). Определить ток, указанный в таблице 1, в заданной по условию схеме с источником тока, использую теорему об эквивалентном генераторе. Начертить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС. Таблица 1
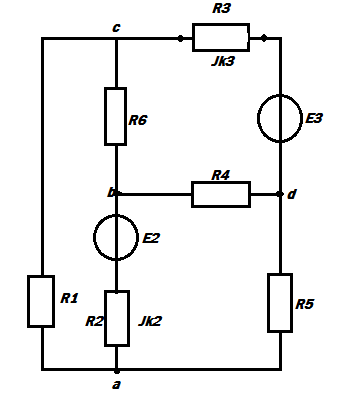 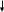 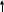       Рисунок 1 – Исходная схема для расчёта Решение: Нарисуем эквивалентную схему. Для упрощения расчётов преобразуем источник тока в источник ЭДС. 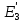 = Jk3·R3 = 1∙5 = 5 В = Jk3·R3 = 1∙5 = 5 ВE3Э = E3 + 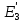 = 30 + 5 = 35 В = 30 + 5 = 35 В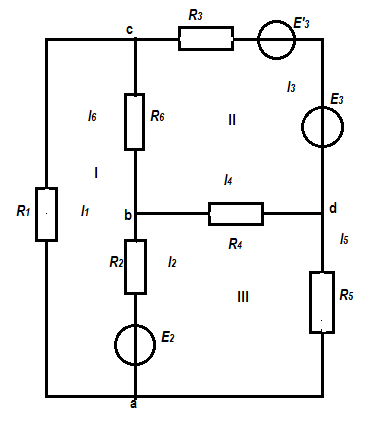          Рисунок 2 – Эквивалентная расчётная схема Анализ схемы: Число узлов p = 4. Число ветвей n = 6. Число уравнений, которое необходимо составить по двум законам Кирхгофа: N1,2 = n = 6. Число уравнений, которое необходимо составить по первому закону Кирхгофа: N1 = p –1 = 4 – 1 = 3. Число уравнений, которое необходимо составить по второму закону Кирхгофа: N2 = N1,2 –N1 = 6 – 3 = 3. Составление системы уравнений по двум законам Кирхгофа Первыйзакон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю. Выбираем условно положительные направления токов (на схеме указаны стрелками). Если ток направлен к узлу, он входит в выражение со знаком «+». Если от узла – со знаком «–». Дляузла «a»: I5 – I2 – I1 = 0 Дляузла«b»: I2 – I4 – I6 = 0 Дляузла«c»:I1 + I6 – I3 = 0 Дляузла«d»: I3+ I4 – I5 = 0 Второй закон Кирхгофа: алгебраическая сумма падений напряжений на всех участках замкнутого контура равна алгебраической сумме ЭДС, действующих в этом контуре. Для составления недостающих уравнений, выбираем направление обхода контура (против часовой стрелки). Все токи на участках, совпадающие с направлением обхода, считаются положительными, несовпадающие – отрицательными. Далее необходимо учитывать правило знаков для ЭДС источников: если направление действия электродвижущей силы в источнике совпадает с направлением обхода участка (стрелка внутри источника), то при подсчёте ЭДС этого источника считается положительной, в противном случае – отрицательной. Составляем уравнения, пользуясь вторым законом Кирхгофа 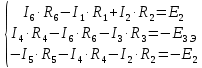 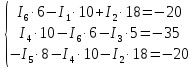 Найдём все токи в ветвях электрической цепи, пользуясь методом контурных токов. Для этого изобразим расчётную схему. Приписываем каждому независимому контуру свой контурный ток.        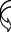      Рисунок 3 – Эквивалентная расчётная схема с контурными токами Система уравнений для этих контурных токов 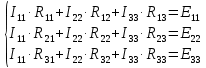 Собственные сопротивления контуров (контурные сопротивления) 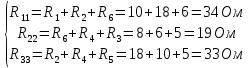 Взаимные сопротивления контуров 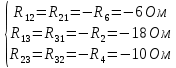 Суммарные ЭДС контуров (контурные ЭДС) 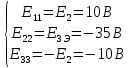 Подставляя численные значения ЭДС, источника тока и сопротивлений, получим систему уравнений: 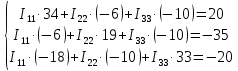 Полученная система уравнений рассчитывается по методу Крамера I11= 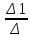 , I22= , I22=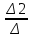 , I33= , I33= , , где Δ–общий определитель системы уравнений. Решим систему трёх уравнений первой степени с тремя неизвестными Δ 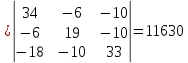 0 Соответствующие контурные определители Δ1, Δ2, Δ3, получаемые из Δ путём замены первого, второго и третьего столбцов столбцом контурных ЭДС, равны: Δ1 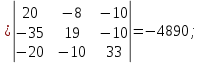 Δ2 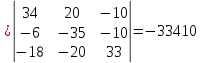 ; ;Δ3 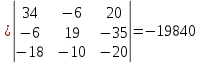 Значение контурных токов I11= 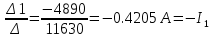 ; ;I22= 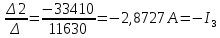 ; ;I33= 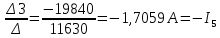 . .Значение токов в ветвях находится как алгебраическая сумма соответствующих контурных токов. 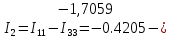 ) )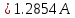 ; ;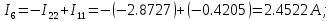 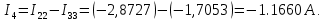 Метод узловых потенциалов Заземлим узел «а». Заземление любой точки схемы свидетельствует о том, что потенциал этой точки принимается равным нулю: φа= 0.  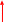      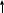 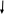  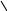 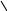  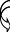 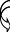 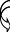  Рисунок 4 – Эквивалентная расчётная схема с заземлением Записываем систему уравнений метода в общем виде 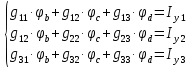 Узловые проводимости с одинаковыми индексами находим как сумму проводимостей всех ветвей, подключенных к узлу с таким же индексом (сумма проводимостей ветвей, сходящихся в узле). 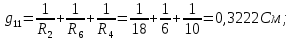 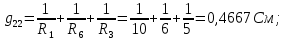 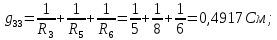 Недиагональная проводимость с разными индексами (например, g12) равна взятой со знаком минус проводимости всех ветвей, соединяющих узлы 1 и 2. 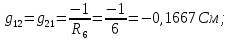 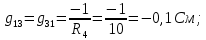 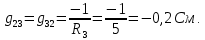 Узловые токи находим, как алгебраическую сумму, подключенных к данному узлу источников напряжения, делённых на сопротивления ветвей, в которых они находятся. Со знаком плюс записываем величину эдс источников, направленных к узлу, и, знак минус, если стрелка ЭДС направлена от узла. 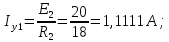 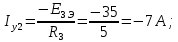 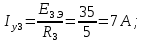 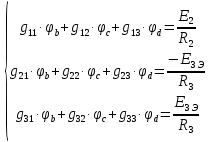 Подставим численные значения 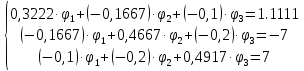 Полученная система уравнений рассчитывается по методу Крамера φb = 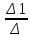 , φc = , φc = 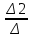 , φd = , φd =  , , где Δ–общий определитель системы уравнений. Решим систему трёх уравнений первой степени с тремя неизвестными Δ 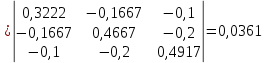 ; ;Соответствующие узловые определители Δ1, Δ2, Δ3, получаемые из Δ путём замены первого, второго и третьего столбцов столбцом узловых токов, равны: Δ1 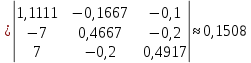 ; ;Δ2 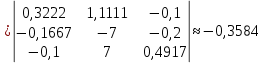 ; ;Δ3 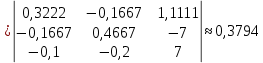 . .Значение потенциалов φb = 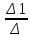 = =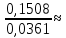 4,176 В; 4,176 В;φc = 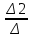 = = 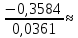 - 9.981 В; - 9.981 В;φd =  = = 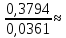 10,51 В. 10,51 В.Значение токов в ветвях I1= 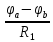 = =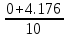 = =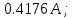 I2= 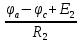 = =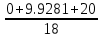 = =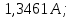 I3= 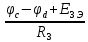 = =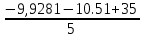 = =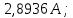 I4= 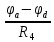 = =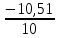 = =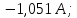 I5= 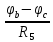 = =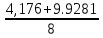 = =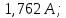 I6= 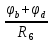 = = 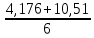 = = 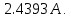 Результаты расчётов двумя методами Таблица 2
Баланс мощностей Алгебраическаясумма мощностей,потребляемых пассивными элементами электрической цепи, должна быть равна алгебраической сумме мощностей,вырабатываемых источниками электрической энергии. 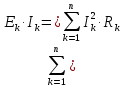 Рассчитываем мощность, потребляемую пассивными элементами электрической цепи 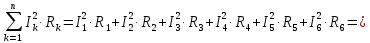 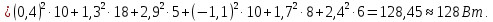 Рассчитаем мощность, выделяемую источниками ЭДС 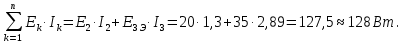 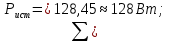 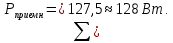 Вывод: баланс мощностей соблюдается. Определим ток I1 методом эквивалентного генератора Размыкаем ветвь с неизвестным током (устраняем резистор R1из исходной схемы), находим напряжение холостого хода Uabxx на зажимах разомкнутой ветви и входное сопротивление Rвх. 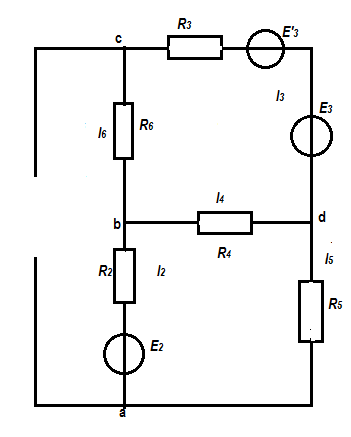      Рисунок 5 – Эквивалентная расчётная схема с разомкнутым током I1 Для определения входного сопротивления Rвх устраняем все источники 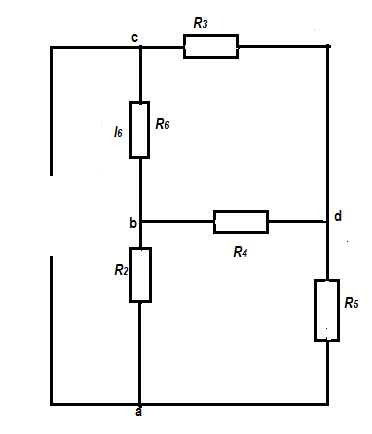 Рисунок 6 – Эквивалентная расчётная схема без источников Uxx  Преобразуем треугольник сопротивлений R6, R3, R4 в звезду Rс, Rd, Rb  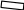   Рисунок 7 – Схема для определения Rвх Найдём величину сопротивлений Rс, Rd, Rb, соединённых по схеме «звезда» 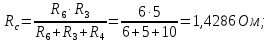 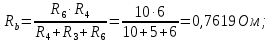 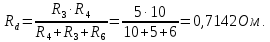 С учётом лучей «звезды» сопротивлений нарисуем эквивалентную схему 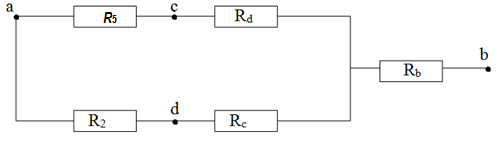 Рисунок 8– Эквивалентная схема для определения входного сопротивления Рассчитываем входное сопротивление 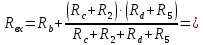 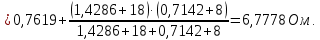 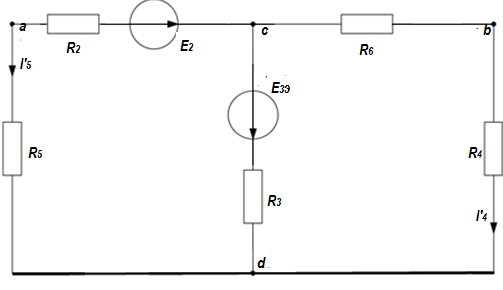 Рисунок 9 – Схема для определения Ucdxx По методу двух узлов определим напряжение 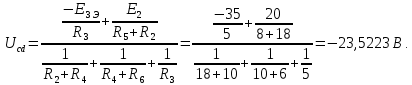 Из выражения: 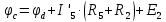 следует, что следует, что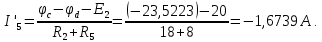 Из выражения: 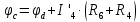 следует, что следует, что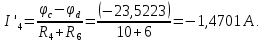 Из выражения: 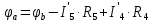 следует, что следует, что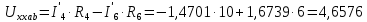 В. В.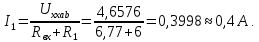 Потенциальная диаграмма для замкнутого контура «amcfkda» Заземлим узел «d», условнопринимая потенциал этой точки равным нулю и обходим контур, содержащий все ЭДС от этой точки. Таким образом φd= 0. 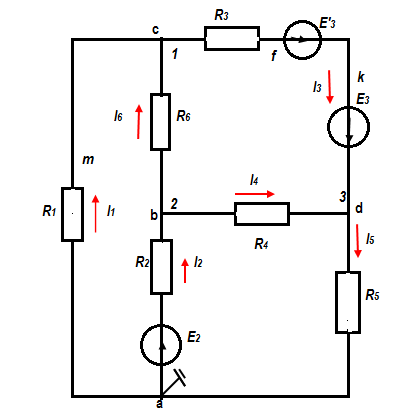    Рисунок 10 – Контур для построения потенциальной диаграммы По методу узловых потенциалов ( 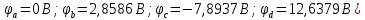 Рассчитываем потенциальную диаграмму 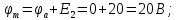 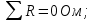 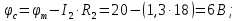 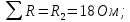 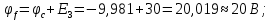 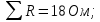 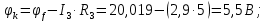 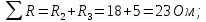 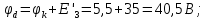 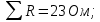 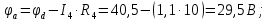 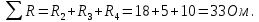 Строим потенциальную диаграмму. На оси абсцисс откладываем сопротивления участков в той последовательности, как они встречаются при обходе контура от узла с нулевым потенциалом. По оси ординат откладываем рассчитанные потенциалы соответствующих узлов. 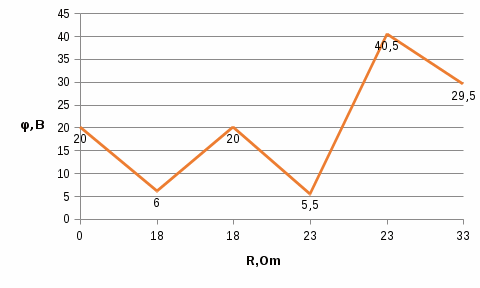 Рисунок 11– Потенциальная диаграмма для выбранного контура |
