Интерполяция. интерполяция. Кусочнолинейная интерполяция
 Скачать 0.73 Mb.
|
|
Кусочно-линейная интерполяция 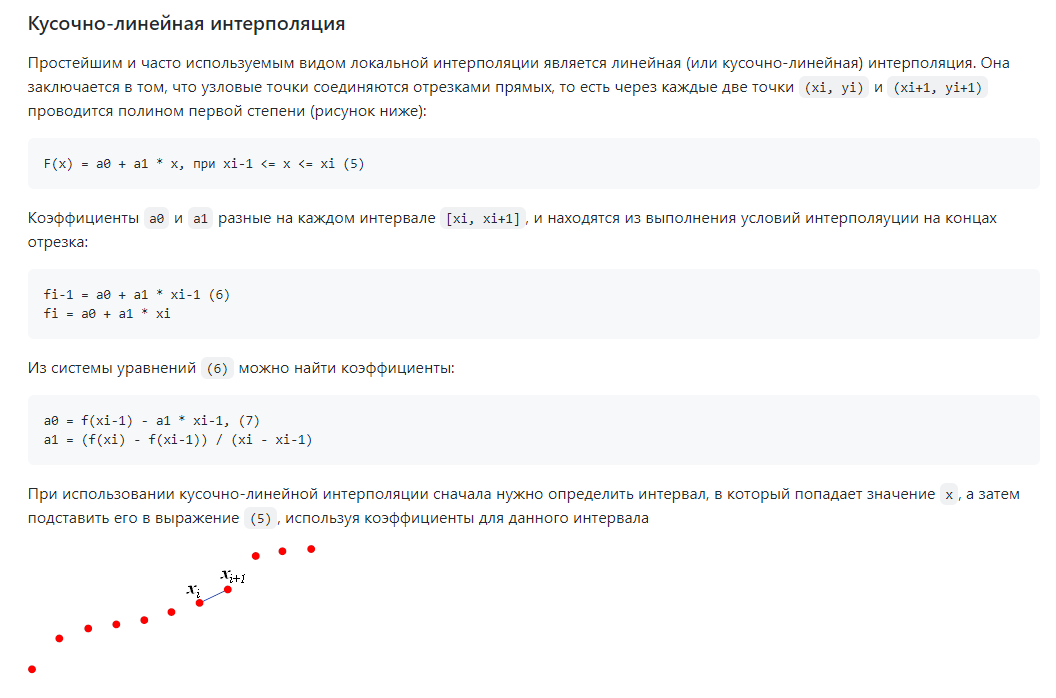 Для функции y=f(x), заданной таблично осуществим кусочно-линейное интерполирование:
Интервал 0 ≤ x ≤ 0,5 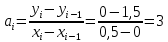 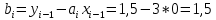 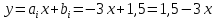 Интервал 0,5 ≤ x ≤ 1 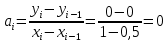 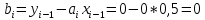 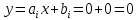 Интервал 1 ≤ x ≤ 2 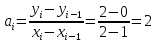 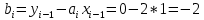 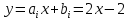 Интервал 2 ≤ x ≤ 3 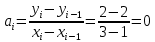 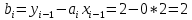 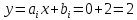 Интервал 3 ≤ x ≤ 4 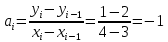 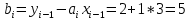 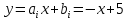 Интервал 4 ≤ x ≤ 5 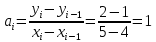 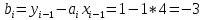 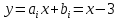 S1(x) = 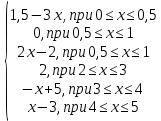 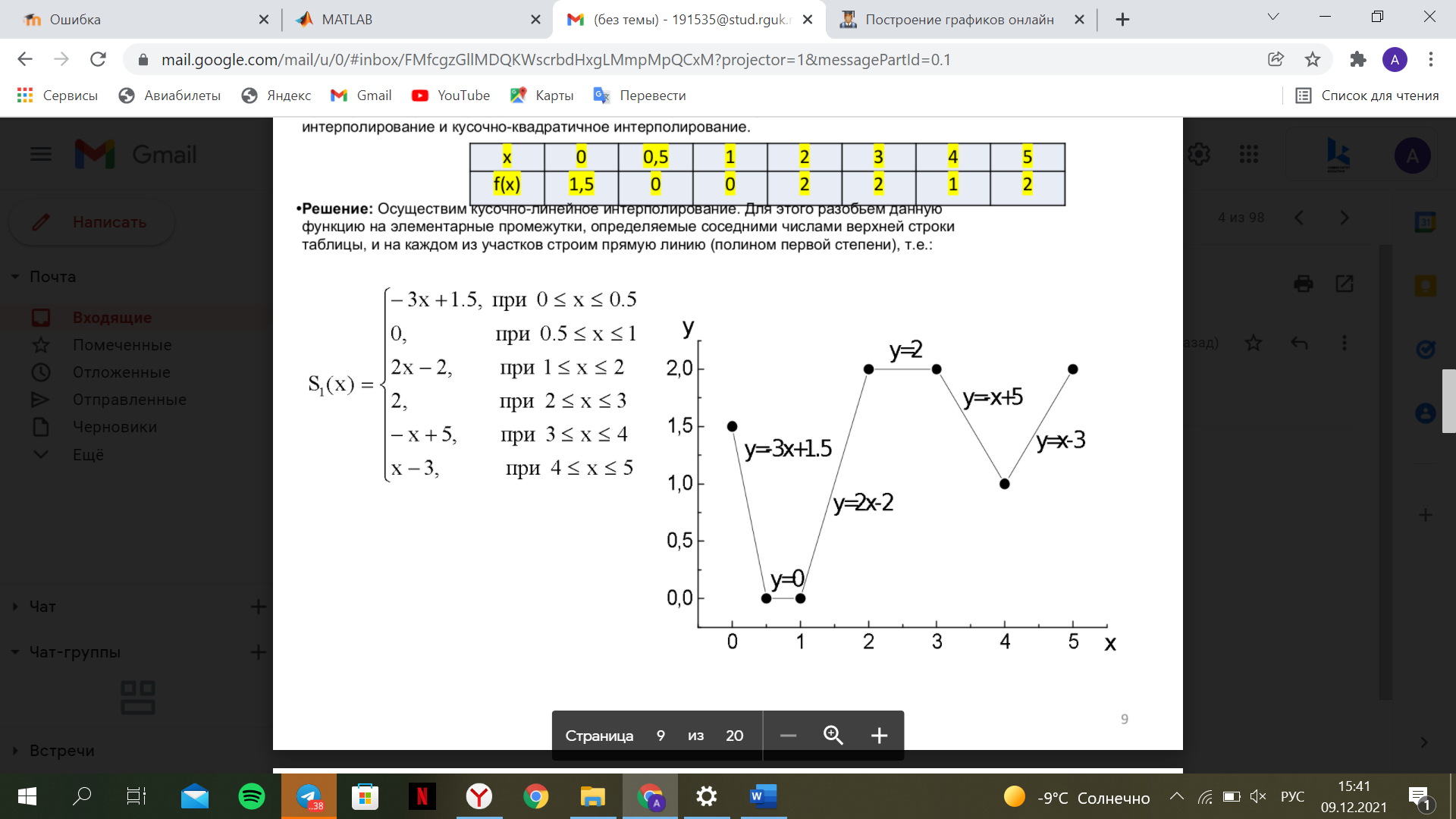 Кусочно-квадратичная интерполяция  Для функции y=f(x) осуществим кусочно-квадратичное интерполирование Рассмотрим тройки известных точек отрезков: [0;1], [1;3], [3;5]. На каждом из отрезков по известным точкам построим полином второй степени На интервале 0 ≤ x ≤1 найдем константы: 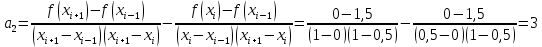 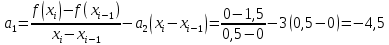 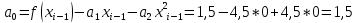 Квадратное уравнение 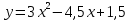 Интервал 1 ≤ x ≤ 3 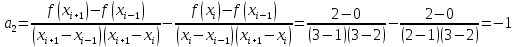 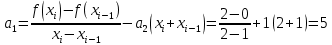 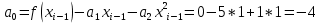 Квадратное уравнение 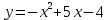 Интервал 3 ≤ x ≤ 5 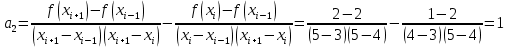 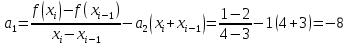 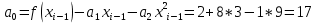 Уравнение 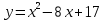 S2(x) = 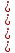 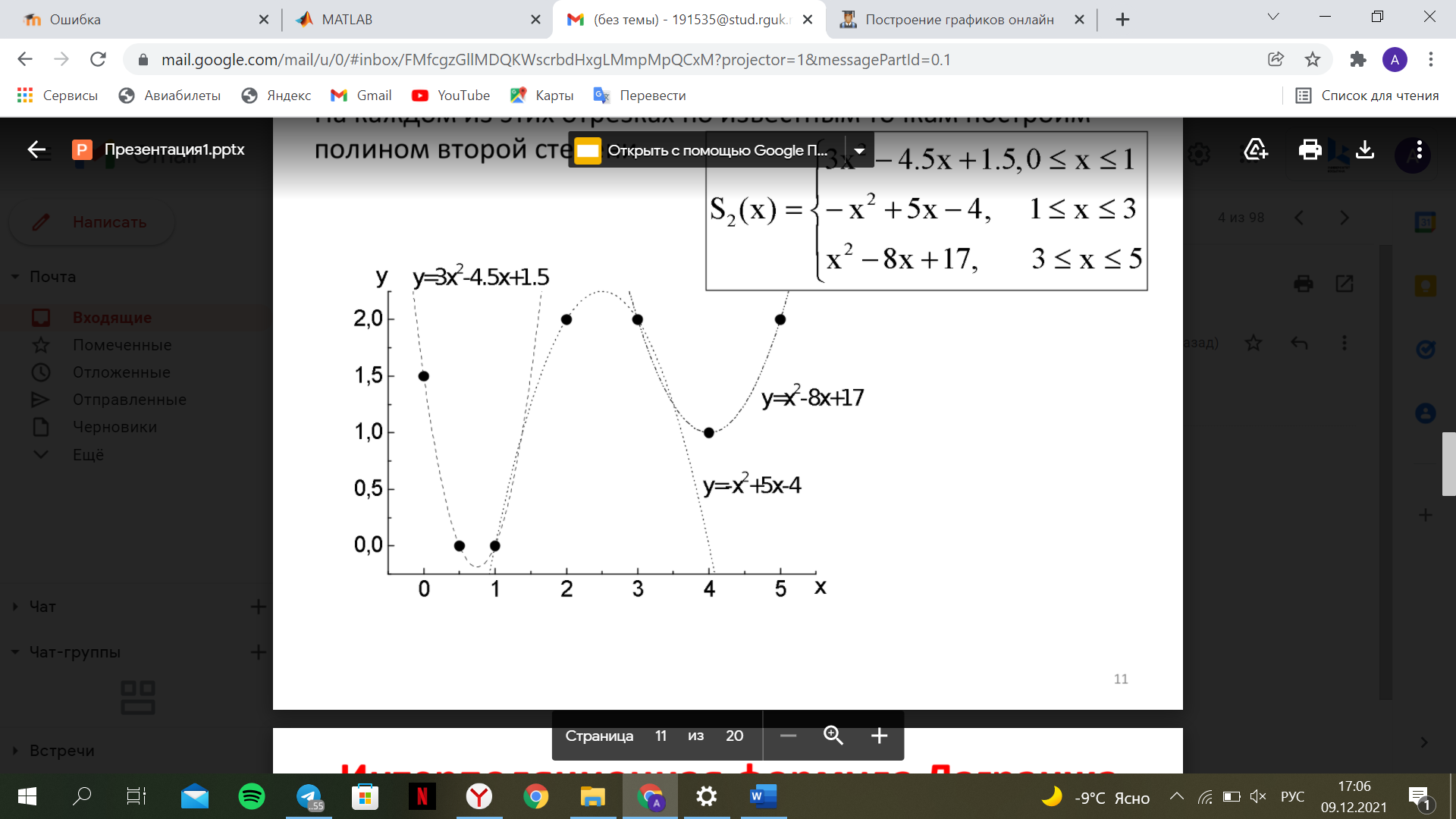 Интерполяционная формула Лагранжа 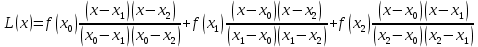 Построим интерполяционный многочлен Лагранжа для функции, заданой таблично:
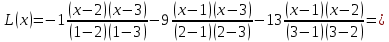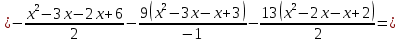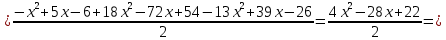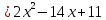    Вывод: интерполяция или интерполирование — приближенное или точное нахождение какой-либо величины по известным отдельным значениям этой же величины, или других величин, с ней связанных. Линейная интерполяция – простейший и часто используемый вид интерполяции. Она состоит в том, что заданные точки с координатами xi , yi при i=0, 1, 2, ... n соединяются прямолинейными отрезками, а функцию y(x) можно приближенно представить в виде ломаной. Квадратичная интерполяция — если интерполирующая функция - многочлен второго порядка, то интерполяция называется квадратичной. Интерполяционный многочлен в форме Лагранжа – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений. |