математика. Математика 1 курс 2 сем. Практическое занятие 6. Квадратные и иррациональные уравнения и неравенства. Метод интервалов. Степенная, показательная и логарифмическая функции. Решение тригонометрических уравнений и неравенств. Производная функции

Название	Квадратные и иррациональные уравнения и неравенства. Метод интервалов. Степенная, показательная и логарифмическая функции. Решение тригонометрических уравнений и неравенств. Производная функции
Анкор	математика
Дата	16.01.2023
Размер	1.2 Mb.
Формат файла
Имя файла	Математика 1 курс 2 сем. Практическое занятие 6.doc
Тип	Программа #888683
страница	1 из 3

1 2 3

Автономная некоммерческая профессиональная образовательная организация «Национальный социально-педагогический колледж»

Программа среднего профессионального образования

44.02.02 Преподавание в начальных классах

Дисциплина: Математика.

Практическое занятие 6

Преподаватель:

Пермь-2022

Темы: Квадратные и иррациональные уравнения и неравенства. Метод интервалов. Степенная, показательная и логарифмическая функции. Решение тригонометрических уравнений и неравенств. Производная функции. Исследование функции с помощью производной. Неопределенный интеграл. Определенный интеграл. Многогранники и площади их поверхностей. Объем многогранников. Элементы математической статистики.

Цель занятия: закрепление навыков решения квадратных, дробно-рациональных и иррациональных уравнений и неравенств, нахождения значений показательных и логарифмических выражений; закрепление навыков решения тригонометрических уравнений и неравенств, а также задач дифференциального исчисления и интегрального исчисления; нахождения площади поверхности и объема многогранника; овладение навыками решения простейших задач математической статистики.

Задание 1.

Решите предложенные уравнения, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):

А)

Это уравнение можно решить, используя равенство рациональной дроби нулю: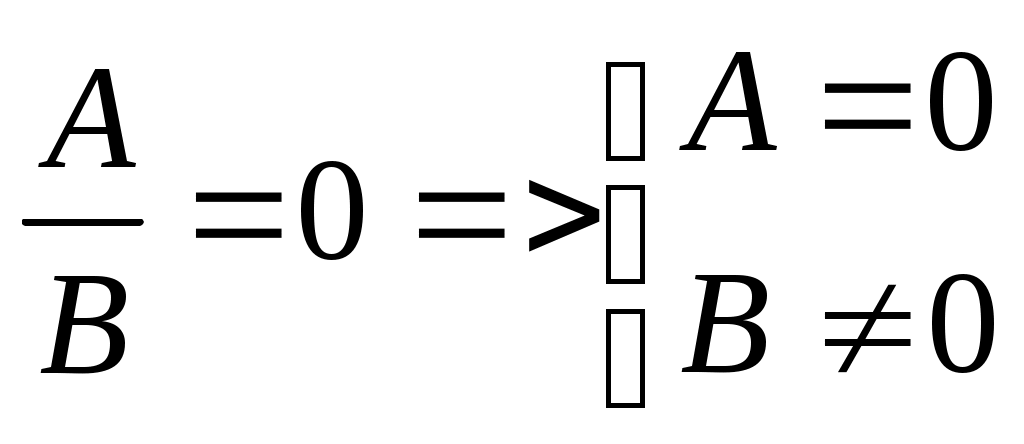

Перенесём всё левую часть уравнения.

Найдем общий знаменатель:

(5x+1)*(x+5)

Умножим обе части уравнения на общий знаменатель и подведём под одну дробь:

Составим систему уравнений и решим её:

Решим первое уравнение. Вынесем общий множитель (2х+6) за скобку:

(2х+6)(х+5)-(5х+1)=0

Раскроем внутренние скобки:

(2х+6)(х+5-5х-1)=0

Сократим необходимое:

(2х+6)(4-4х0=0

Вынесем за скобку общие множители из каждой скобки:

2*(х+3)*4(1-х)=0

Уравнение равно нулю, если обе части уравнения или одна из них равно нулю:

Х+3=0 или 1-х=0

Х₁=-3 х₂=1

Решим второе неравенство.

(х+5)(5х+1)

Найденные значения х₁, х₂ – корни уравнения, не обращают дробь в ноль.

Ответ: -3;1.

Б)

Решим уравнение, используя формулу. Возведём во вторую степень обе части уравнения:

Возведём снова во вторую степень:

12-4х=16. Решим полученное уравнение.

-4х=16-12

-4х=4

Х=-1

Подставим в исходное уравнение:

2=2 - верно

Ответ: -1.

Задание 2.

Решите предложенные неравенства методом интервалов, подробно описывая ход решения:

А) 2-х-3х²<0

Найдем корни многочлена. Для этого приравняем левую часть неравенства к нулю.

2-х-3х²=0

А=-3, b= -1, c=2

D=b²-4ac=(-1)²-4*(-3)*2=1+24=25

Отметим найденные корни на числовой оси и нарисуем интервалы

Определим знак («+» или «-») на одном интервале. Например, при х=0 (это средний интервал). Подставим х=0 в левую часть неравенства:

2-0-3*0=2>0 – положительное число, значит на среднем интервале будет стоять знак «+». На остальных интервалах знаки будут чередоваться.

Осталось записать интервалы с «-». Так как в неравенстве стоит <0. Таких два интервала.

Ответ: (-∞;1)

(

;+∞)

Б)

Приравняем левую часть неравенства к нулю.

Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нолю (т.к. на нуль делить нельзя). Составим систему уравнений и решим её.

Решим первое уравнение. Уравнение произведения равно нулю, если один из множителей многочлена равен нулю.

Х(х+6)=0

Х²=0 или х+6=0

Х₁=0 х₂=-6

Решим второе неравенство.

Отметим найденные числа на числовом промежутке и нарисуем интервалы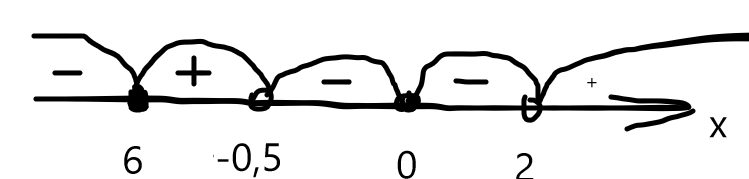

Закрасим кружочки, где значение дроби обращается в нуль. Подставим значения для определения знаков постоянства на промежутке.

При х=-7:

Значит самый левый промежуток будет иметь знак «-».

Подставим значение х=1

, значит четвертый интервал будет иметь знак «-».

Подставим значение х=-1

, значит второй интервал будет иметь знак «+».

Подставим значение х=-0,2

, значит третий интервал будет иметь знак «-».

Подставим значение х=3.

, значит пятый интервал будет иметь знак «+».

Осталось записать интервалы с «+». Ответ:

∞)

Задание 3.

Найдите значение выражений, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):

Решение:

В знаменателе разложим на множители согласно правилу действий со степенями

Вычислим значения степени с одинаковым основанием. Для этого вычтем из степени числителя степень знаменателя, по правилу деления степенных чисел с одним основанием

ⁿ^-^m

Запишем промежуточные расчеты.

Представим

в виде значения со степенью

В числителе сложим показатели степени по правилу умножения степенных чисел с одним основанием:

Для этого приведем их к общему знаменателю.

Далее из показателя степени числителя вычтем показатель степени знаменателя (по правилу деления показателя степени чисел с одинаковым основанием):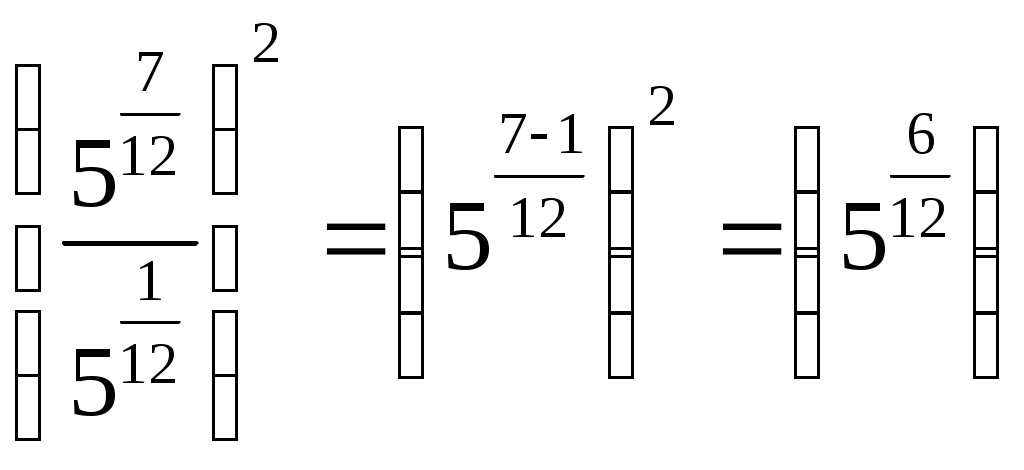

²

Сократим показатель степени и представим в виде числа с корнем.

Ответ: 5.

По определению логарифма:

Подставим полученные значения в выражение, Таким образом 4+2-4=2.

Ответ:2.

Воспользуемся формулой log_aa=1 и представим число 1 в виде логарифма:

Воспользуемся формулой:

.Для этого разделим два подлогарифмических выражения с одним основанием и в результате представим подлогарифмические выражении в виде числа, равному основанию, со степенью:

Воспользуемся формулой:

.Для этого показатель степени подлогарифмического выражения вынесем впреди логарифма, как множитель:

Воспользуемся формулой логарифма с новым основанием для первого логарифма и впоследствии сократим:

Ответ:1.

Задание 4

Решите предложенные уравнения, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты

Решение:

Представим вторую часть уравнения в виде числа со степенью:

Тогда показатели степени с одним основанием равны:

Сделаем проверку:

Верно

Ответ:5.

Разложим показательные числа на множители:

Перенесём в левую часть уравнения все числа и переменные:

Сделаем замену. Пусть 4^x=t

Получаем квадратное уравнение:

Домножим уравнение на 4:

Разложим квадратное уравнение на множители, для этого(–t) представим в виде (-2t+t):

t-2=0 или t+1=0

t=2 t=-1

Сделаем обратную замену:

Представим пол логарифмическое выражение в виде показательного числа:

По определению логарифма и по формуле вычислим:

У нас, а=x-3, b=2

Х-3=3, x=3+3, x=6

Сделаем проверку, для этого подставим в исходное уравнение.

2=2-верно.

Ответ: 6.

Воспользуемся формулой:

Тогда:

Если,

, значит под логарифмическое выражение из уравнения будет равно 2:

Перенесём всё в левую часть уравнения:

Приведём к одному знаменателю:

Решим уравнение, как систему уравнений. Так как дробь равна нулю, когда знаменатель не равен нулю, а числитель равен нулю:

Сделаем проверку, для этого подставим в исходное уравнение:

Воспользуемся формулой:

1=1-верно

Ответ:

.

Задание 5.

Решите предложенные неравенства, подробно описывая ход решения (указывайте формулы и положения, которыми пользуетесь, записывайте промежуточные результаты):

Решение:

Это показательное уравнение имеет вид:

Запишем неравенство в таком виде:

Логарифмирование:

Теперь возьмём от обоих частей неравенства логарифм по основанию 3. Мы имеем право это делать, так как обе части неравенства больше нуля. Основание логарифма больше единицы, поэтому знак неравенства не изменится.