Квант. Квантовая оптика. Лабораторный практикум.. Квантовая оптика
 Скачать 3.97 Mb. Скачать 3.97 Mb.
|
|
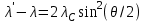 | | (1.1) |
где λ и
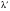 - соответственно, длины волн до и после рассеяния; θ – угол рассеяния; λС - так называемая комптоновская длина волны электрона, равная λС = 2,4·10-12 м.
- соответственно, длины волн до и после рассеяния; θ – угол рассеяния; λС - так называемая комптоновская длина волны электрона, равная λС = 2,4·10-12 м.
Рис.1.1. Схема комптоновского рассеяния
Эффект Комптона представлен на диаграмме рис. 1.1, иллюстрирующей закон сохранения импульса при упругом рассеянии фотонов на свободных электронах. До столкновения электрон покоится. Его импульс ре =0. После столкновения электрон отдачи имеет импульс
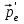 ;
; 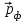 и
и 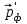 - импульс налетающего и рассеянного фотонов;
- импульс налетающего и рассеянного фотонов; 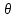 - угол рассеяния фотона; φ – угол, под которым летит электрон отдачи относительно направления падающего фотона (угол отдачи).
- угол рассеяния фотона; φ – угол, под которым летит электрон отдачи относительно направления падающего фотона (угол отдачи). В рентгеновском диапазоне длин волн и для гамма-излучения энергия фотонов соизмерима с собственной энергией электрона
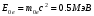 . Так как при рассеянии фотонов такой высокой энергии электрон может приобрести значительную кинетическую энергию, при рассмотрении эффекта Комптона необходимо использовать законы релятивистской механики.
. Так как при рассеянии фотонов такой высокой энергии электрон может приобрести значительную кинетическую энергию, при рассмотрении эффекта Комптона необходимо использовать законы релятивистской механики.Если
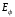 и
и 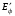 энергия фотона, а
энергия фотона, а 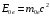 и
и 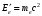 - энергия электрона, соответственно, до и после столкновения, то исходная система уравнений, описывающих упругое столкновение фотона со свободным электроном включает закон сохранения энергии
- энергия электрона, соответственно, до и после столкновения, то исходная система уравнений, описывающих упругое столкновение фотона со свободным электроном включает закон сохранения энергии 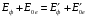 или или 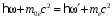 , , | | (1.2) |
где
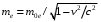 , и закон сохранения импульса (рис.1.1)
, и закон сохранения импульса (рис.1.1) 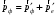 или или 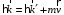 , , | | (1.3) |
где
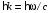 ,
,  . Для фотона как частицы с нулевой массой покоя энергия и импульс связаны соотношением
. Для фотона как частицы с нулевой массой покоя энергия и импульс связаны соотношением 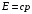 . Тогда закон сохранения примет вид
. Тогда закон сохранения примет вид 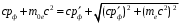 . . | | (1.4) |
Из закона сохранения импульса по теореме косинусов получим:
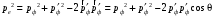 . . | | (1.5) |
Возведем в квадрат левую и правую часть закона сохранения энергии (1.4):
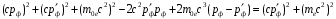 . . | | |
Учитывая (1.5) и упрощая выражение, запишем
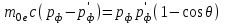 , или
, или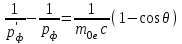 .
.Тогда, подставляя
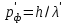 и
и 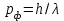 , имеем
, имеем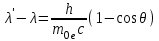 . (1.6)
. (1.6)Коэффициент
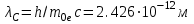 носит название комптоновской длины волны.
носит название комптоновской длины волны.МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ
Запустить программу Labvisual ФЯЛ-02.
С помощью пульта управления установить необходимый угол измерения, при этом активный датчик отмечается световым сигналом. Выбрать удобную для измерения интенсивность сигнала.

Рис.1.2. Внешний вид установки «Наблюдение эффекта Комптона».
Пульт управления
Регистрирующее устройство.
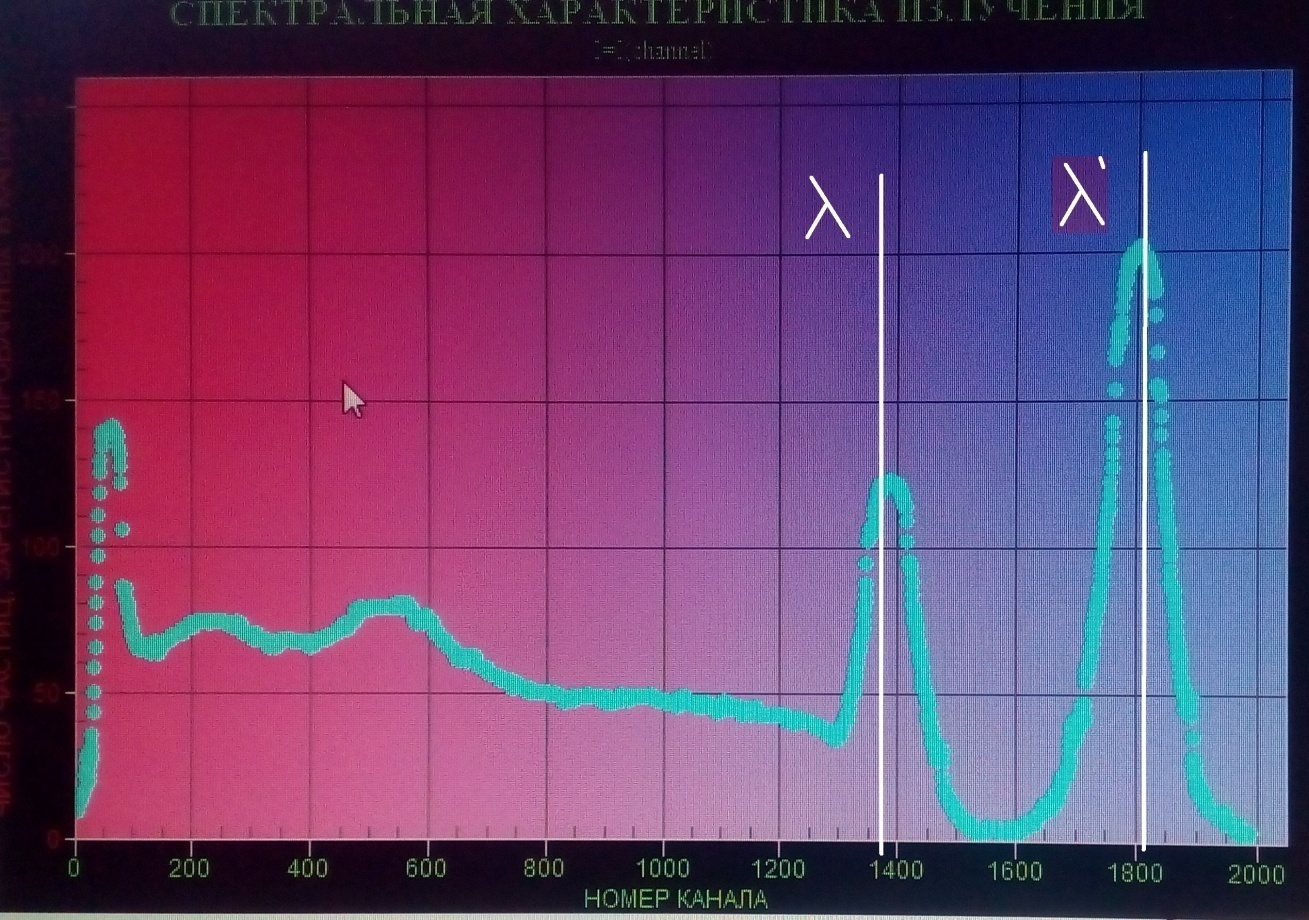
Рис. 1.3. Вид окна сканирования спектра.
Таблица 1.1.
| № | θ | (1-cosθ) | λ | 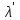 | λC | <λC> |
| 1 | 00 | | | | | |
| 2 | 100 | | | | | |
| 3 | 200 | | | | | |
| 4 | 300 | | | | | |
| 5 | 400 | | | | | |
| 6 | 500 | | | | | |
| 7 | 600 | | | | | |
| 8 | 700 | | | | | |
| 9 | 800 | | | | | |
| 10 | 900 | | | | |
В меню программы выбрать «Автоматическое сканирование и набор спектра». Нажать «Автоскан+» или «Автоскан-». Справа поставить флажок в окне «Показать набираемый спектр» и нажать «Визуализировать данные».
Измерить длины волн
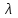 и
и 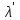 , как показано на рис.1.3. Заполнить соответствующую строку таблицы 1.1.
, как показано на рис.1.3. Заполнить соответствующую строку таблицы 1.1.Повторить пп.2-4 для других углов измерения, согласно Вашему варианту.
Вычислить и записать в табл. 1.1 величины (1 – cos). Построить график зависимости изменения длины волны (
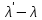 ) для каждой серии измерений.
) для каждой серии измерений.Определите по наклону графика значение комптоновской длины волны электрона
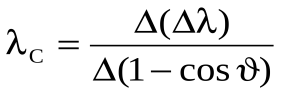 .
.Запишите результат и сделайте вывод.
Вопросы и задания для самоконтроля
Что означает «корпускулярно-волновой дуализм»? Опишите модели, с помощью которых описываются свойства квантовых частиц.
Что такое луч? Что такое гармоническая волна? Сформулируйте связь между характеристиками электромагнитной волны в волновой и квантовой моделях.
Опишите модель взаимодействия падающего рентгеновского фотона и свободного электрона вещества. Какие законы сохранения выполняются при взаимодействии фотона с электроном в эффекте Комптона?
Сравните поведение фотонов после взаимодействия с электронами в эффекте Комптона и фотоэффекте.
Что такое комптоновская длина волны частицы?
Почему эффект Комптона не наблюдается при рассеянии фотонов на электронах, сильно связанных с ядром атома?
Как меняется энергия фотона при его комптоновском рассеянии? Что происходит с электроном после рассеяния на нем фотона?
Чем отличается масса частицы от массы покоя? Когда они совпадают?
Напишите формулу импульса фотона.
Изобразите чертеж взаимодействия фотона с электроном в эффекте Комптона. Выведите формулу (1.6).
Напишите формулу для комптоновской длины волны электрона.
ЛАБОРАТОРНАЯ РАБОТА № 2
ОПЫТ ФРАНКА И ГЕРЦА
ЦЕЛЬ РАБОТЫ:
изучение процесса возбуждения атомов металла электронами, измерение первого потенциала возбуждения.
КРАТКАЯ ТЕОРИЯ
Еще в античные времена Демокрит высказал идею о том, что Вселенная состоит из маленьких неделимых частиц — атомов. Это представление о строении вещества сохранилось до конца XIX столетия, когда достоверно было установлено, что в состав каждого атома входят электроны. Приоритет в открытии электрона принадлежит английскому физику Джозефу Джону Томсону. Тогда же стало известно, что атом электрически нейтрален. Следовательно, отрицательный заряд электронов должен компенсироваться положительным зарядом неизвестных частиц, входящих в заряд атома.
В 90-х годах XIX века получила широкое распространение модель атома Томсона в виде однородной положительной сферической среды, в которой, как изюминки в булке, рассредоточены отрицательно заряженные электроны. Атомная модель Томсона подобна кексу. Однако вскоре автор «кексовой» модели высказал предположение о нестатическом положении электронов в атоме.
Наиболее реальной представлялась ядерная или планетарная модель атома Э. Резерфорда, предложенная английским физиком в 1911г. Планетарная модель явилась результатом выполненных Э. Резерфордом и его сотрудниками экспериментов по рассеянию α-частиц. Опыты состояли в следующем. Пучок положительно заряженных α-частиц направляется на тонкий лист золотой фольги. За фольгой находился экран, покрытый сцинтиллятором — веществом, которое испускает свет в той точке, в которую ударялась α-частица. Исходя из модели Томсона, следовало ожидать, что α-частицы не будут отклоняться на большие углы, так как электроны гораздо легче α-частиц. И, действительно, опыты показали, что большинство α-частиц свободно проходили сквозь лист фольги, как если бы он представлял собой в основном пустое пространство. И все же часть α-частиц отклонялась на небольшие углы, причиной чего было взаимодействие с положительным зарядом атома. Но неожиданным и ошеломляющим оказалось то, что небольшое количество α-частиц рассеивалось на большие углы, достигающие 180°. Такое могло происходить только в том случае, если положительно заряженные α-частицы испытали отталкивание массивного положительного заряда, сконцентрированного в малой области пространства.
По модели Э. Резерфорда атом состоит из массивного, положительно заряженного ядра, в котором сосредоточено 99,94 % массы атома. Величина положительного заряда оценивается произведением ze, где z— порядковый атомный номер химического элемента в таблице Менделеева; е — элементарный заряд. Вокруг ядра внутри сферы с наружным диаметром 10-10 м по замкнутым эллиптическим орбитам вращается z электронов, образуя электронную оболочку атома. Электроны не могут покоиться в атоме, так как в этом случае они упали бы на ядро под действием кулоновского притяжения. По оценкам Э. Резерфорда, размеры ядра должны быть порядка 10-15—10-14м. Сравнивая размеры ядра и атома, приходим к выводу о том, что электроны должны находиться от ядра на расстоянии в 104 -105 больше, чем размер ядра. И отсюда второй вывод: основную часть атома составляет пустое пространство.
Недостаток модели Э. Резерфорда состоит в невозможности объяснить факт исключительной устойчивости атома: во-первых, при столкновениях с другими атомами; во-вторых, по законам классической физики вращение электронов вокруг ядра не может быть устойчивым, так как оно должно сопровождаться электромагнитным излучением, как всякое ускоренное движение заряженных частиц. По законам классической физики электроны, двигаясь по окружности, обладают центростремительным ускорением. Центростремительная, сила, удерживающая электрон на орбите радиусом r, представляет кулоновскую силу притяжения электрона к ядру:
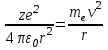 ,
,где εо= 8,85 • 10-12Ф/м — электрическая постоянная;
 ; v— скорость электрона на орбите. На создание электромагнитного поля расходуется энергия. Энергия электрона должна постепенно убывать, а вместе с ней и скорость вращения электрона вокруг ядра. Электрон в конце концов должен упасть на ядро. Однако атомы — достаточно устойчивые образования и могут существовать миллиарды лет. В-третьих, по модели Э. Резерфорда спектр излучения атома должен быть сплошным. Опыты же показали, что спектр излучения конкретного атома является дискретным.
; v— скорость электрона на орбите. На создание электромагнитного поля расходуется энергия. Энергия электрона должна постепенно убывать, а вместе с ней и скорость вращения электрона вокруг ядра. Электрон в конце концов должен упасть на ядро. Однако атомы — достаточно устойчивые образования и могут существовать миллиарды лет. В-третьих, по модели Э. Резерфорда спектр излучения атома должен быть сплошным. Опыты же показали, что спектр излучения конкретного атома является дискретным.Нильс Бор пришел к убеждению в том, что планетарная модель атома в основном верна и что законы классической физики неприменимы к внутриатомным процессам. Усовершенствовав модель Э. Резерфорда, Бор создал квантовую теорию строения атома, в основу которой положены три постулата, названные постулатами Бора.
Согласно первому постулату Бора атом может длительное время (по атомной шкале времени) находиться только в определенных, так называемых стационарных состояниях, которые характеризуются дискретными значениями энергии Е1, Е2, Е3, ... В этих состояниях, вопреки классической электродинамике, атом не излучает энергию.
Второй постулат (правило частот) гласит, что при переходе атома из стационарного состояния с большей энергией Е2 в стационарное состояние с меньшей энергией Е1 происходит излучение кванта света (фотона) с энергией
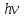 :
: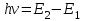 (2.1)
(2.1)Третий постулат Бора: переход электрона с одной стационарной орбиты на другую сопровождается излучением или поглощением атомом кванта энергии
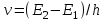 .
.Иными словами, частота излучаемых или поглощаемых электромагнитных волн зависит не от частоты вращения электрона, а от разности энергий разрешенных состояний атома.
Опыты Франка и Герца дали прямое доказательство дискретности атомных состояний, т. е. принесли экспериментальное подтверждение постулатов Бора.В 1925 г. за открытие законов столкновений электронов с атомами Джеймс Франк и Густав Людвиг Герц были удостоены Нобелевской премии.
Идея опытов заключается в следующем. При неупругих столкновениях электрона с атомом происходит передача энергии от электрона атому. Если внутренняя энергия атома изменяется непрерывно, то атому может быть передана любая порция энергии. Если же состояния атома дискретны, то его внутренняя энергия при столкновении с электроном должна изменяться также дискретно - на значения, равные разности внутренней энергии атома в стационарных состояниях.
 | Следовательно, при неупругом столкновении электрон может передать атому лишь определенные порции энергии. Измеряя их, можно определить значения внутренних энергий стационарных состояний атома. |
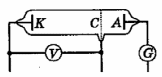
| Рис.2.1. Схема установки Франка и Герца |
Принципиальная схема установки, примененной Франком и Герцем, представлена на рис. 2.1. В баллоне с парами ртути под давлением порядка 1 мм рт. ст. (130 Па) имелись три электрода: К - катод, С - сетка и А - анод. Электроны, испускаемые горячим катодом вследствие термоэлектронной эмиссии, ускорялись разностью потенциалов U между катодом и сеткой. Величину U можно было плавно менять. Между сеткой и анодом создавалось слабое тормозящее поле с разностью потенциалов около 0,5 В.
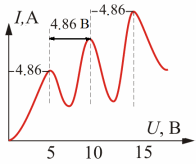 | Таким образом, если электрон, проходящий сквозь сетку, имеет энергию меньше 0,5 эВ, то он не долетит до анода. Электроны, долетевшие до анода, образуют анодный ток, доступный измерению. На опыте исследовалась вольт-амперная характеристика (рис. 2.2). Оказалось, что при увеличении ускоряющей разности потенциаловU вплоть до 4,86 В сила анодного тока возрастает монотонно, проходит через максимум (4,86 В), затем резко падает и возрастает вновь. |
| Рис.2.2. Вольт-амперная характеристика триода для Hg в опыте Франка и Герца |
Дальнейшие максимумы наблюдаются при 2·4,86=9.72 В; 3·4,86=14.58 В и т. д.
Такой вид кривой объясняется тем, что первое возбужденное состояние атома ртути отстоит от основного по шкале энергий на
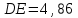 эВ, и атомы действительно могут поглощать лишь дискретные порции энергии, равные этой величине. При энергии электронов, меньшей 4,86 эВ, они испытывают только упругие столкновения и передают атомам малую часть своей энергии (пропорциональную отношению массы электрона m к массе атома M, а т.к. m << M, то потеря кинетической энергии ничтожна). Когда же ускоряющее напряжение U становится равным 4,86 В, электроны начинают испытывать вблизи сетки неупругие столкновения, отдавая атому ртути всю энергию, и уже не могут преодолеть тормозящую разность потенциалов между сеткой и анодом. Значит на анод могут попасть только те электроны, которые не испытали неупругого столкновения. Поэтому, начиная с ускоряющего напряжения 4,86 В, анодный ток будет уменьшаться.
эВ, и атомы действительно могут поглощать лишь дискретные порции энергии, равные этой величине. При энергии электронов, меньшей 4,86 эВ, они испытывают только упругие столкновения и передают атомам малую часть своей энергии (пропорциональную отношению массы электрона m к массе атома M, а т.к. m << M, то потеря кинетической энергии ничтожна). Когда же ускоряющее напряжение U становится равным 4,86 В, электроны начинают испытывать вблизи сетки неупругие столкновения, отдавая атому ртути всю энергию, и уже не могут преодолеть тормозящую разность потенциалов между сеткой и анодом. Значит на анод могут попасть только те электроны, которые не испытали неупругого столкновения. Поэтому, начиная с ускоряющего напряжения 4,86 В, анодный ток будет уменьшаться.При дальнейшем росте ускоряющего напряжения достаточное число электронов после неупругого столкновения успевает приобрести энергию, необходимую для преодоления тормозящего поля за сеткой. Начинается новое возрастание силы тока. Когда ускоряющее напряжение увеличится до значения 2·4,86 В, электроны после одного неупругого столкновения достигают сетки с энергией 4,86 эВ, достаточной для второго неупругого столкновения. При втором неупругом столкновении электроны опять теряют почти всю свою энергию и не достигают анода. Поэтому анодный ток начинает опять уменьшаться (второй максимум на рис. 2.2). Аналогично объясняются и последующие максимумы. Практически, однако, следующие максимумы менее резко выражены и постепенно кривая становится просто плавно возрастающей, т.к. статистически для одного электрона вероятность испытать каждое следующее неупругое столкновение с атомом уменьшается.
Аналогичные опыты были проведены в дальнейшем с атомами других газов. И для них были получены характерные разности потенциалов, соответствующие переходу атома из основного состояния в ближайшее возбужденное. Такие характерные разности потенциалов называют первыми потенциалами возбуждения.
Таблица 2.1. Значения потенциалов возбуждения газов.
| Элемент | He | Ne | Ar | Kr | Xe | Hg | Na | K | Cs |
| Uвозб , В | 20,9 | 16,6 | 11,6 | 10,0 | 8,5 | 4,9 | 2,1 | 1,6 | 1,4 |
Итак, все опыты такого рода приводят к заключению, что состояние атомов изменяются лишь дискретно.
Опыты Франка и Герца подтверждают также и второй постулат Бора - правило частот. Оказывается, что при достижении ускоряющего напряжения 4,86 В пары ртути начинают испускать ультрафиолетовое излучение с длиной волны 253,6 нм. Это излучение связано с обратным переходом атомов ртути из первого возбужденного состояния в основное. Используя это значение, по правилу частот можно получить значение первого потенциала возбуждения, хорошо согласующееся с предыдущими измерениями:
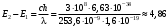 эВ (2.2)
эВ (2.2)К вышеизложенному необходимо добавить два замечания. Во-первых, поскольку столкновения ускоренных электронов с атомами носят статистический характер, т.е. существует определенная вероятность возбуждения атомов как до первого, так и до второго и других потенциалов возбуждения. Следовательно, на графике вольт-амперной характеристики теоретически могут появляться и другие максимумы, соответствующие более высоким потенциалам возбуждения. Но если концентрация атомов в объеме достаточно велика, то такие максимумы возникать не будут, т.к. длина свободного пробега электрона между двумя неупругими соударениями с атомами будет недостаточной для приобретения такой кинетической энергии, которой бы хватило для возбуждения более высоких энергетических состояний.
Во-вторых, в силу того, что электроды, как правило, изготавливаются из разных металлов, между ними дополнительно возникает внешняя контактная разность потенциалов. Ее наличие приводит смещению кривой зависимости анодного тока от ускоряющего напряжения влево или вправо на величину этой контактной разности потенциалов. При этом интересующее нас расстояние между соседними максимумами на графике не меняется.
Несколько причин приводят к тому, что провалы экспериментальной зависимости I(U) не являются идеально резкими, и происходит некоторый сдвиг максимумов на кривой в сторону меньших энергий:
1.Существенный разброс энергии электронов из-за наличия области пространственного заряда в прикатодной области и высокой температуры термоэмиссионного катода (для данного случая справедлива максвелловская функция распределение частиц по скоростям и энергиям);
2. Падение напряжения на катоде прямого накала при протекании по нему тока накала, приводящее к различным значениям потенциала для разных точек катода;
3. Зависимость сечения возбуждения атомов ртути либо инертного газа от энергии электрона;
4. Разброс продольной составляющей скорости электронов после неупругого столкновения, величина которой определяет возможность преодоления задерживающего поля анод-сетка.

