Квант. Квантовая оптика. Лабораторный практикум.. Квантовая оптика
 Скачать 3.97 Mb.
|
|
Приборы и оборудование. Метод возбуждения атомов потоком электронов особенно пригоден для инертных газов и паров металла, поскольку атомы этих веществ не обладают электронным сродством, т.е. не проявляют склонности к захвату электронов и образованию отрицательных ионов. В данной работе используется трехэлектродная лампа с парами ртути.
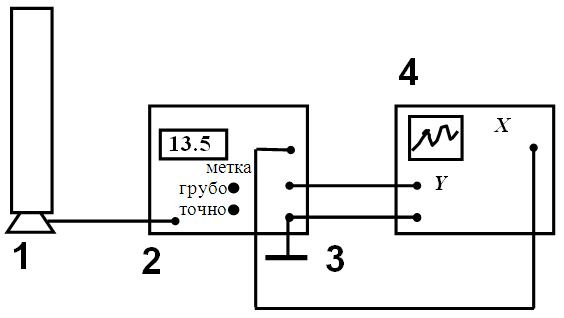
Это же напряжение подается на вход Х 3 осциллографа 4, создавая развёртку луча на экране. На вход У осциллографа подаётся напряжение, пропорциональное анодному току триода. Тогда зависимость У(Х) в определенном масштабе представляет собой искомую функциональную связь I = f(U). Масштабы изображения по осям Х и У можно легко изменять, пользуясь соответствующими регулировками усиления осциллографа. В результате на экране наблюдается вольт-амперная характеристика триода, повторяющая форму рисунка 2.2. Порядок выполнения работы.
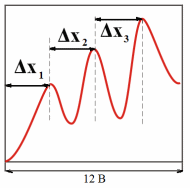
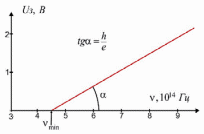
где N – число клеток экрана осциллографа по оси абсцисс. 1. Включить источник питания 2 в цепи сетка-анод. Установить напряжение UСА = 2,5 В). 2. Включить осциллограф в сеть. Установить на передней панели осциллографа масштабные коэффициенты 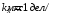 ,  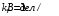. 3. С помощью осциллограммы определить первый и второй потенциал возбуждения, как показано на рис.2.4, и заполнить таблицу 2.2. Оценить погрешности δх и δU как погрешность прямых измерений, а δλ – как погрешность косвенных измерений. Таблица 2.2.
4. Используя формулу 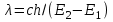 и зная величину первого потенциала возбуждения, определить длину волны испускаемого атомами ртути излучения.Вопросы и задания для самоконтроля В чем сущность опытов Франка и Герца? Какие основные выводы можно сделать на основании опытов Франка и Герца? Какие столкновения электронов с атомами называются упругими и неупругими? На каких участках графика вольт-амперной характеристики имеют место упругие, а на каких – неупругие столкновения? С какой целью на анод подается задерживающее напряжение, и из каких соображений оно выбирается? Что такое первый потенциал возбуждения? Какое состояние атома называется основным, а какое – возбужденным? Чем объясняется тот факт, что даже при отсутствии подачи ускоряющего напряжения UСК наблюдается анодный ток в цепи нагрузки? В чем причина возникновения смещения графиков UR= f(UСК) с изменением величины задерживающего напряжения? При каком ускоряющем потенциале будет наблюдаться резкое падение анодного тока в аналогичном опыте, если лампу заполнить атомарным водородом? Почему не наблюдается свечения ртути в объеме лампы несмотря на то, что возбужденные атомы снова переходят в основное состояние и при этом испускают кванты электромагнитной энергии? Почему на данной установке невозможно измерить третий, четвертый и т.д. потенциалы возбуждения ртути? ЛАБОРАТОРНАЯ РАБОТА № 3 ФОТОЭФФЕКТ ЦЕЛЬ РАБОТЫ: Изучение основных законов внешнего фотоэффекта на основе измерения световой и вольтамперной характеристик вакуумного фотоэлемента. КРАТКАЯ ТЕОРИЯ Фотоэлектрический эффект был открыт в 1887 году немецким физиком Г.Герцем и в 1888–1890 годах экспериментально исследован А.Г.Столетовым. Наиболее полное исследование явления фотоэффекта было выполнено Ф.Ленардом в 1900 г. К этому времени уже был открыт электрон (1897 г., Дж. Томсон), и стало ясно, что внешний фотоэффект состоит в вырывании электронов из вещества под действием падающего на него света.
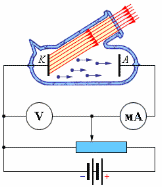
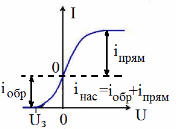
На рис.3.2 изображены типичные кривые такой зависимости, полученные при двух значениях интенсивности светового потока, падающего на катод. По мере увеличения напряжения U фототок постепенно возрастает, т.е. все большее количество фотоэлектронов достигает анода. Пологий характер кривых показывает, что электроны вылетают из катода с различными скоростями. Максимальное значение тока Iнас – фототок насыщения – определяется таким значением U, при котором все электроны, испускаемые катодом, достигают анода: Iнас. = en, где n – число электронов, испускаемых катодом в 1 секунду, e заряд электрона.
максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой v. Для каждого вещества существует красная граница фотоэффекта, т. е. минимальная частота v0 света (зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен. Тщательные измерения показали, что ток насыщения Iн прямо пропорционален интенсивности падающего света. Трудности объяснения фотоэффекта Как можно было бы объяснить фотоэффект с точки зрения классической электродинамики и волновых представлений о свете? Известно, что для вырывания электрона из вещества требуется сообщить ему некоторую энергию A, называемую работой выхода электрона. В случае свободного электрона в металле - это работа по преодолению поля положительных ионов кристаллической решётки, удерживающего электрон на границе металла. В случае электрона, находящегося в изолированном атоме, работа выхода есть работа по разрыву связи электрона с ядром. В переменном электрическом поле световой волны электрон начинает совершать колебания. И если энергия колебаний превысит работу выхода, то электрон будет вырван из вещества. Однако в рамках таких представлений невозможно понять второй и третий законы фотоэффекта. Действительно, почему кинетическая энергия выбитых электронов не зависит от интенсивности излучения? Ведь чем больше интенсивность, тем больше напряжённость электрического поля в электромагнитной волне, тем больше сила, действующая на электрон, тем больше энергия его колебаний и с тем большей кинетической энергией электрон вылетит из катода. Логично? Логично. Но эксперимент показывает иное. Откуда берётся красная граница фотоэффекта? Чем «плохи» низкие частоты? Казалось бы, чем больше интенсивность света, тем больше сила, действующая на электроны; поэтому даже при низкой частоте света электрон рано или поздно будет вырван из вещества — когда интенсивность достигнет достаточно большого значения. Однако красная граница ставит жёсткий запрет на вылет электронов при низких частотах падающего излучения. Кроме того, непонятна безынерционность фотоэффекта. При освещении катода излучением сколь угодно слабой интенсивности (с частотой выше красной границы) фотоэффект начинается мгновенно — в момент включения освещения. Между тем, казалось бы, электронам требуется некоторое время для «расшатывания» связей, удерживающих их в веществе, и это время «раскачки» должно быть тем больше, чем слабее падающий свет. Аналогия такая: чем слабее вы толкаете качели, тем дольше придётся их раскачивать до заданной амплитуды. Выглядит логично, но опыт — единственный критерий истины в физике! — этим доводам противоречит. Так на рубеже XIX и XX столетий в физике возникла тупиковая ситуация: электродинамика, предсказавшая существование электромагнитных волн и великолепно работающая в диапазоне радиоволн, отказалась объяснять явление фотоэффекта. Выход из этого тупика был найден Альбертом Эйнштейном в 1905 году. Он нашёл простое уравнение, описывающее фотоэффект. Все три закона фотоэффекта оказались следствиями уравнения Эйнштейна. Главная заслуга Эйнштейна состояла в отказе от попыток истолковать фотоэффект с позиций классической электродинамики. Эйнштейн привлёк к делу гипотезу о квантах, высказанную Максом Планком пятью годами ранее. Электромагнитная энергия излучается и поглощается не непрерывно, а дискретно отдельными порциями — квантами. Энергия кванта пропорциональна частоте излучения:
Cоотношение (3.1) называется формулой Планка, а коэффициент пропорциональности h — постоянной Планка. Успешность гипотезы Планка наводила на мысль, что законы классической физики неприменимы к малым частицам вроде атомов или электронов, а также к явлениям взаимодействия света и вещества. Подтверждением данной мысли как раз и послужило явление фотоэффекта. Гипотеза Планка говорила о дискретности излучения и поглощения электромагнитных волн, то есть о прерывистом характере взаимодействия света с веществом. При этом Планк считал, что распространение света — это непрерывный процесс, происходящий в полном соответствии с законами классической электродинамики. Эйнштейн пошёл ещё дальше: он предположил, что свет в принципе обладает прерывистой структурой: не только излучение и поглощение, но также и распространение света происходит отдельными порциями — квантами, обладающими энергией E = hν. Планк рассматривал свою гипотезу лишь как математический трюк и не решился опровергнуть электродинамику применительно к микромиру. Кванты электромагнитного излучения (в частности, кванты света) стали впоследствии называться фотонами. Таким образом, свет состоит из особых частиц — фотонов, движущихся в вакууме со скоростью c. Каждый фотон монохроматического света, имеющего частоту ν, несёт энергию hν. Фотоны могут обмениваться энергией и импульсом с частицами вещества; в таком случае мы говорим о столкновении фотона и частицы. В частности, происходит столкновение фотонов с электронами металла катода. Поглощение света — это поглощение фотонов, то есть неупругое столкновение фотонов с частицами (атомами, электронами). Поглощаясь при столкновении с электроном, фотон передаёт ему свою энергию. В результате электрон получает кинетическую энергию мгновенно, а не постепенно, и этим объясняется безынерционность фотоэффекта. Уравнение Эйнштейна для фотоэффекта есть не что иное, как закон сохранения энергии. На что идёт энергия фотона hν при его неупругом столкновении с электроном? Она расходуется на совершение работы выхода A по извлечению электрона из вещества и на придание электрону кинетической энергии:
Слагаемое mv2/2 называется максимальной кинетической энергией фотоэлектронов. Почему максимальной? Электроны в металле могут быть свободными и связанными. Свободные электроны «гуляют» по всему металлу, связанные электроны «сидят» внутри своих атомов. Кроме того, электрон может находиться как вблизи поверхности металла, так и в его глубине. Ясно, что максимальной кинетическая энергия фотоэлектрона будет в том случае, когда фотон попадёт на свободный электрон в поверхностном слое металла — тогда для выбивания электрона достаточно одной лишь работы выхода. Во всех других случаях придётся затрачивать дополнительную энергию — на вырывание связанного электрона из атома или на «протаскивание» глубинного электрона к поверхности. Эти лишние затраты приведут к тому, что кинетическая энергия вылетевшего электрона окажется меньше. Энергия квантовых частиц часто измеряется во внесистемных единицах «электрон-вольтах». 1 электрон-вольт (эВ) = 1.6·10-19 Дж. Красной границей фотоэффекта называется минимальная частота излучения, при которой всё ещё наблюдается фотоэффект
Таблица 3.1. Значения работы выхода электронов для различных материалов фотокатодов
У большинства чистых металлов «красная граница» лежит в ультрафиолетовой части спектра.
Запирающим (задерживающим) напряжением называется минимальное тормозящее напряжение между анодом вакуумной лампы (фотоэлемента) и фотокатодом, при котором отсутствует ток в цепи этой лампы, т.е. фотоэлектроны не долетают до анода. При таком напряжении кинетическая энергия электронов у катода равна потенциальной энергии электронов у анода
Описание установки Внешний фотоэффект используется в приборах, которые называются фотоэлементами (ФЭ). В данной работе используется вакуумные фотоэлементы Ф-08 и Ф-13. 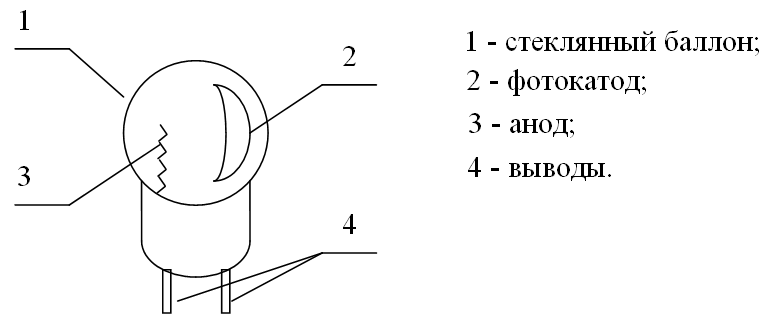 Рис.3.4. Схематичное изображение фотоэлемента Фотоэлемент Ф-13 измерительный вакуумный с массивным мультищелочным катодом на алюминиевой пластине, с предварительно нанесенным слоем сурьмы. Оптический вход торцевой Диаметр катода 27±1 мм Диаметр колбы без штенгеля, не более 40 мм Высота фотоэлемента без штырьков 50±2 мм Область спектральной чувствительности 350 — 700 нм Спектральная чувствительность на длине волны 600 нм составляет не менее 17 % от максимума, на длине волны 700 нм — не менее 1 % от максимума. Рабочее напряжение 300 В при импульсных потоках излучения и 100 В при постоянном во времени световом потоке. Относительная неравномерность чувствительности катода не превышает ±30 % от его среднего значения. Среднее отклонение фототока от его среднего значения в серии 20 световых импульсов при длительности (3-10) мкс не превышает ±2 % при повторных импульсах, происходящих раз в 60 сек. Внешний вид экспериментальной установки изображен на рис.3.5.  Рис.3.5. Экспериментальная установка К корпусу 1, в котором находится источник излучения, прикреплен усилитель фототока, на верхнюю крышку которого устанавливаются сменные фотоприемники с фотоэлементами Ф-8 или Ф-13 (2). При установке фотоприемников их приемное окно совмещают с выходным окном осветителя и закрывают при помощи бленды. 3 - измерительный блок. Порядок работы 1. Получить у преподавателя или инженера номера фотоэлемента и используемых светофильтров. Установить на объект исследования фотоприемник с исследуемым фотоэлементом и соединить бленду осветителя с окном фотоэлемента. 2. Включить объект исследования выключателем «СЕТЬ» на его передней панели. Дайте лампе осветителя прогреться в течение 15 минут. 3. Подключите сетевые шнуры измерительного устройства к сети, нажмите тумблер «СЕТЬ» на его задней панели. При этом должен загореться индикатор «ОБРАТНАЯ». На индикаторе вольтметра должны установиться нули (допускается индикация до значения 2 младшего разряда). После пятиминутного прогрева ручками «УСТАНОВКА НОЛЯ» на объекте исследования установить нулевое значение на индикаторе амперметра. ВНИМАНИЕ! РЕЖИМ РАБОТЫ УСТАНОВКИ ПРЕРЫВИСТЫЙ – ЧЕРЕЗ КАЖДЫЕ 45 МИНУТ РАБОТЫ ПЕРЕРЫВ 15 МИНУТ. 4. Установить необходимый светофильтр. 5. С помощью кнопки «ПРЯМАЯ-ОБРАТНАЯ» выбрать режим измерения обратной вольт-амперной характеристики. 6. Изменяя значения напряжения с помощью кнопок «+» и «-», измерьте вольт-амперную характеристику в обратном направлении. Не забудьте указать знак напряжения и силы тока. 7. Выбрать режим «ПРЯМАЯ» и повторить пп.5,6 для прямой вольтамперной характеристики. Результаты измерения занести в таблицу 3.2. Таблица 3.2.
8. Снять прямые и обратные вольт-амперные характеристики с другими светофильтрами и фотоэлементами, согласно Вашему варианту. По окончании измерений отключить питание установки. 9. Выбрав удобный масштаб, построить на миллиметровой бумаге семейство измеренных вольт-амперных характеристик. Для каждой из них определить токи насыщения и задерживающий потенциал, как показано на рис.3.6. Значения занести в таблицу 3.3. Вычислить работу выхода для каждого фотоэлемента. Используя таблицу 3.1, определить материал катода. Таблица 3.3.
Вопросы и задания для самоконтроля В чём заключается сущность явления фотоэффекта? Объясните принцип работы фотоэлемента с внешним фотоэффектом. Что такое «красная граница» фотоэффекта? Чем обусловлено её наличие и положение на шкале длин волн? Объясните причину различия вольтамперных характеристик в прямом направлении для разных световых потоков. При каких условиях возникает ток насыщения? Изобразите вольтамперную характеристику фотоэлемента, включенного в обратном направлении. Объясните ее. ЛАБОРАТОРНАЯ РАБОТА № 4 ИЗУЧЕНИЕ СПЕКТРА АТОМА ВОДОРОДА И ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА ЦЕЛЬ РАБОТЫ: Провести калибровку спектрометра; исследовать спектр атомарного водорода и неона; вычислить постоянную Ридберга. КРАТКАЯ ТЕОРИЯ Оптические свойства атомов определяются состоянием валентных электронов. Согласно современным представлениям, электроны в атомах могут находиться лишь в неких стационарных состояниях, которым соответствуют строго определенные дискретные значения энергии, называемые энергетическими уровнями. В простейшем случае, в атоме водорода имеется единственный электрон, который является валентным электроном. Состояние атома в квантовой механике описывается волновой функцией φn, его энергия Еn. В случае простейшего атома – атома водорода, состоящего из протона и электрона, квантовая механика позволяет получить точные решения уравнения Шредингера
где m – масса электрона, Е – полная энергия, 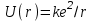 - энергия взаимодействия электрона с ядром, е – заряд электрона, 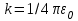 ,  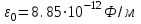- электрическая постоянная. Решения уравнения (4.1) для атома водорода являются набором дискретных уровней энергии. Для связанных состояний (Еn<0):
где 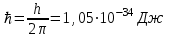 , n =1,2,3,…- главное квантовое число.С ростом числа n уровни энергии атома сближаются, в пределе при 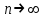 дискретный спектр приближается к непрерывному, а квантовая система к классической. Это и есть принцип соответствия Бора, который позволяет выразить энергию электронов в атоме через фундаментальные постоянные. Для простоты Бор принял, что в атоме водорода электроны вращаются вокруг протона по окружности радиусом r с циклической частотой ω:
Согласно правилу квантования момента импульса электрона в атоме:
Решение уравнений (4.3) и (4.4) дает выражение для радиусов круговых орбит электронов в атоме водорода:
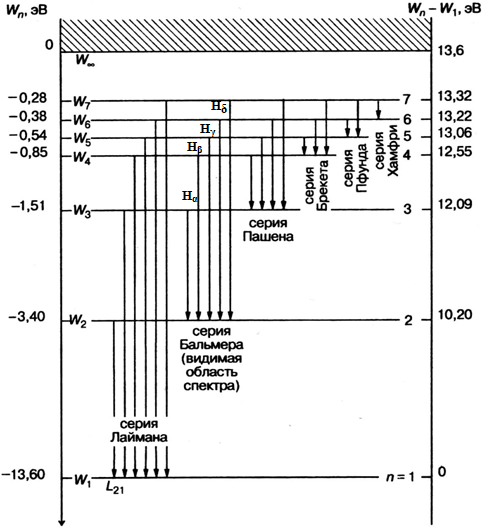 Рис.4.1. Энергетическая диаграмма атома водорода Таким образом, при переходе атома водорода из состояния n2 c энергией Е2 в состояние n1 с энергией Е1 действует правило частот Бора:
то есть испускается фотон с частотой ω и длиной волны λ
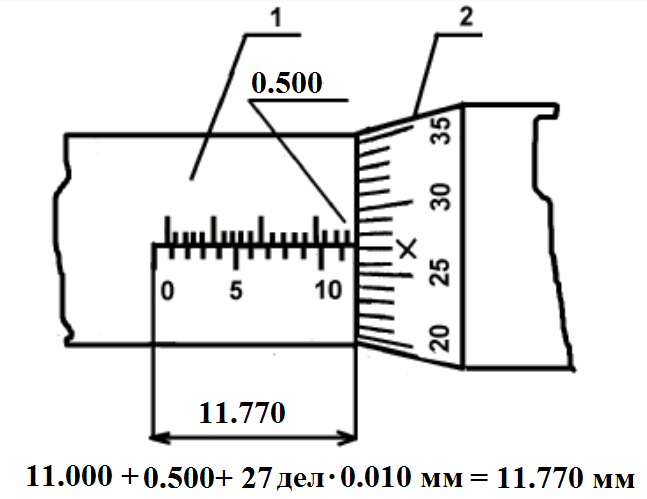
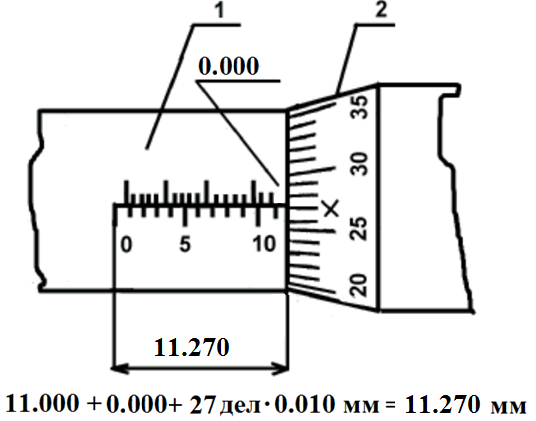
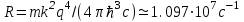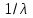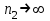Здесь введено обозначение  - постоянная Ридберга. Формула (4.8) называется формулой Бальмера-Ритца. В этой формуле с увеличением n2 и n1 разность между волновыми числами  уменьшается, стремясь при  к предельному значению 0. При этом линии сближаются, и уменьшается их интенсивность. Совокупность длин волн (или частот), излучаемых телом, называют спектром излучения этого тела. Как мы видим, вследствие квантования энергетических уровней электронов в атомах атомарные спектры излучения состоят из дискретного набора длин волн (частот). Такие спектры называются линейчатыми. Совокупность спектральных линий, т.е. длин волн или частот, соответствующих переходам на один и тот же энергетический уровень n1 образует серию линий: - совокупность переходов в основное состояние (n1 =1) образует серию Лаймана; - переходы в состояние с n1 =2 образуют серию Бальмера; - переходы в состояние с n1 =3 образуют серию Пашена. Визуально мы можем наблюдать только серию Бальмера: для водорода – n1 = 2, n2 = 3,4,5…(рис.4.1). Выполнение работы: Внешний вид установки для определения спектральных характеристик атомов показан на рис. 4.2. На оптической скамье 1 соосно установлены источник света (поочередно ртутная, неоновая и водородная лампы) и приемник-анализатор 3 с микрометрическим винтом 4, задающим исследуемую длину волны, и окуляром для наблюдения 5. Измерения с помощью микрометрического винта Микрометрический винт имеет два отсчетных устройства. Первое отсчетное устройство состоит из шкалы с ценой деления 0,500 мм, нанесенной на стебле 1 , как показано на рис.4.3, и указателя, которым является торец барабана 2. Второе отсчетное устройство состоит из шкалы, с ценой деления 0,010 мм, нанесенной на конусной поверхности барабана 2, и указателя в виде продольного штриха, нанесенного на стебле 1. Шаг микровинта S = 0,500 мм, следовательно, одному обороту микровинта и жестко скрепленного с ним барабана соответствует линейное перемещение торца барабана на одно деление, равное 0,500 мм. Круговая шкала барабана имеет число делений n=50 и следовательно, поворот барабана с микровинтом на одно деление относительно продольного штриха стебля 1 рис.2 будет соответствовать величине 0.500/50 10 мкм. Это цена деления прибора. Для проведения измерений производят отсчеты по двум отсчетным устройствам и суммируют их. Примеры отсчета показаны на рис.4.3.  Рис.4.2. Вид установки для измерения постоянной Ридберга
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, 
, 
.
.
.
, 
,
.
.
.
,
,
.
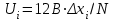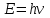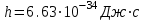
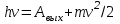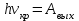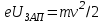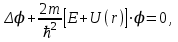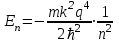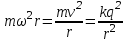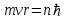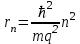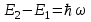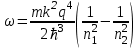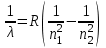