Призма Френеля. ЛабаАвито6. Лабараторная работа 6 Определение длины световой волны при помощи бипризмы Френеля по дисциплине оптика
 Скачать 2.32 Mb. Скачать 2.32 Mb.
|
|
Лабараторная РАБОТА №6 Определение длины световой волны при помощи бипризмы Френеля по дисциплине «ОПТИКА» Направление «» Студента Калининград 2023 Цель работы: Экспериментально определить длины световых волн, пропускаемых светофильтрами. Приборы и принадлежности: виртуальная оптическая скамья, вклюающая: источник света со щелевой диафрагмой, светофильтры, бипризму Френеля, собирающую линзу, окуляр-микрометр. Описание виртуальной установки 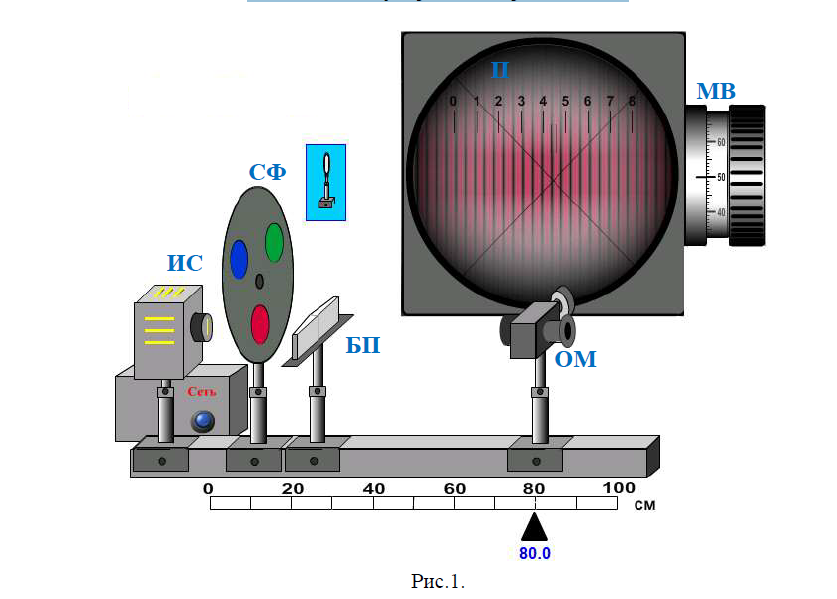 Бипризма БП представляет собой две одинаковые прямоугольные призмы с малыми преломляющими углами, сложенные своими основаниями. Пучок света, падающий на бипризму от источника света ИС с диафрагмой в виде щели, вследствие преломления в бипризме, разделяется на два перекрывающихся пучка, исходящие как бы от двух мнимых источников. За бипризмой, во всей области наложения пучков света, будет наблюдаться интерференционная картина в виде чередующихся параллельных светлых и темных полос (рис. 1). В случае белого света полосы будут радужными, что затрудняет наблюдение. Поэтому в установке используется нохроматический источник света. Длина волны света определяется одним из трех светофильтров СФ, установленных на турели. Для наблюдения и измерения интерференционной картины используется окуляр-микрометр ОМ, увеличенное поле зрения которого П показано вверхнем правом углу установки. Измерение производится с помощью микрометрического винта МВ, как описано ниже. Для определения расстояния между мнимыми источниками между оку- ляр-микрометром и бипризмой помещают собирающую линзу Л, после чего в поле зрения окуляр-микрометра появляется несфокусированное изображе- ние двух мнимых источников (щелей). Перемещением линзы вдоль оптиче- ской скамьи добиваются получения их четкого изображения в поле зрения окуляр-микрометра (рис.2).    Обработка экспериментальных результатов. 1.
2. Запустите ролик с флэш-анимацией (виртуальная установка Biprism.swf). 3. Кликнув по кнопке «Сеть», включите осветитель. В поле зрения окуляр- микрометра возникнет интерференционная картина в виде чередующихся светлых и темных полос. 4. Установите на оптическую скамью линзу кнопкой и, передвигая ее, добейтесь как можно более четкого изображения двух мнимых источников в поле зрения окуляр-микрометра. Занесите значения l (положение окуляр-микрометра) и f (разность положений окуляр-микрометра и линзы) в таблицу. 5. Измерьте расстояние между мнимыми источниками D с помощью окуляр микрометра. Для этого поместите визир сначала на изображение одной, а затем другой щели, и найдите разность координат. Занесите значение D в таблицу. 6. Для измерения ширины интерференционной полосы x удалите линзу с оптической скамьи кнопкой . В поле зрения окуляр-микрометра вновь возникнет интерференционная картина. НЕ ПЕРЕМЕЩАЙТЕ ОКУЛЯР- МИКРОМЕТР ДО ЗАВЕРШЕНИЯ ИЗМЕРЕНИЙ. 7. Для повышения точности измерения ширины полосы измерьте ширину группы из пяти соседних полос x5. Ширину одной полосы x вычислите по формуле x = x5 /5 и занесите это значение в таблицу. 8. Установите последовательно два оставшихся светофильтра и повторите для каждого из них пункт 7. Пункты 4-6 можно не повторять, так как фокусное расстояние линзы не зависит от длины волны. 9. Вычислите и занесите в таблицы значения , погрешностей и средних величин по формулам (3), (4), (5) для всех светофильтров. (3) 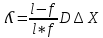 (4)Ꜫ= 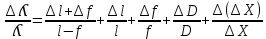 (5) 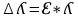 Вывод : в ходе лабораторной работы экспериментально определил длины световых волн, пропускаемых светофильтрами ,их значения близки к значениям в интернете . ЭЛЕКТРОМАГНЕТИЗМ 1) Магнитное поле — поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения; магнитная составляющая электромагнитного поля. 2)  3)   4) Закон Био-Савара-Лапласа гласит: Магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока. B ⇀ = ∑ B ⇀ i i. Элементарный участок d l с током I создает магнитную индукцию: B = μ 0 4 π I d l sin α r 2. Здесь альфа — угол между радиусом-вектором и направлением тока в проводнике. 5)   6)  Для определения положения точки Р проведем координатную ось х вдоль оси симметрии, а начало отсчета поместим в центр контура. При этом расстояние R от точки А до точки Р будет связано с координатой х последней соотношением  Найдем вектор dB магнитной индукции ноля, создаваемого выделенным элементом тока dl в точке Р. По определению векторного произведения из закона Био - Савара - Лапласа следует, что вектор dB перпендикулярен и вектору dl , и вектору R . При этом с учетом того,  что векторы dl и R образуют прямой угол, модуль вектора dB будет равен Так как рассматриваемая система обладает осевой симметрией, вектор В магнитной индукции поля, создаваемого всем контуром, на оси симметрии будет направлен вдоль этой оси. Следовательно, только проекция на ось х этого вектора будет отлична от нуля во всех точках этой оси:  где В - модуль вектора магнитной индукции. В силу принципа суперпозиции проекция на ось х вектора В будет  где dBx - проекция на ось х вектора dB . Используя подобие прямоугольных треугольников на рис. 6.9, находим, что  Подставив выражение (6.23) в формулу (6.22), с учетом (6.21) получим  Все величины под знаком интеграла не зависят от того, где на контуре С расположен векторный элемент dl , и могут быть вынесены за интеграл. Так как интеграл от dl равен длине 2тга окружности, придем к формуле  Подставив в эту формулу выражение (6.20), получим следующую зависимость магнитной индукции от координаты х точки Р:  7)  8) Земля в целом представляет собой огромный шаровой магнит. Магнитное поле Земли имеет внутриземное происхождение. Ядро Земли является жидким и состоящим из железа; в нем циркулируют круговые токи, которые и порождают земное магнитное поле: вокруг токов всегда есть магнитное поле. Оно не является симметричным. Магнитные бури — это значительные изменения магнитного поля Земли под действием усиленного солнечного ветра, в результате вспышек на Солнце и сопровождающих их выбросов потоков заряженных частиц.  \ \ 9) Тангенциальный гальванометр - один из первых гальванометров, использовавшихся для измерения электрического тока. Он работает с помощью компаса, который используется для сравнения магнитного поля создаваемого неизвестным током с магнитным полем Земли. Свое название он получил от тангенциального закона магнетизма, в котором говорится, что тангенс угла наклона магнитной стрелки пропорционален соотношению сил двух перпендикулярных магнитных полей. 10)   |
