Оптическое устройство. Лабораторная работа Исследование оптического анализатора спектра
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 2. Исследование оптического анализатора спектра Вариант 4 Цель работы: Изучение структуры и принципа работы оптического анализатора пространственного спектра, а также возможностей его применения для моделирования диаграмм направленности плоских апертур. 1 Краткие теоретические сведения Из теории дифракции известно, что поле излучателя в дальней зоне в плоскости, перпендикулярной оптической оси, можно представить как преобразование Фурье возбуждающего поля на излучателе только для точек вблизи оптической оси, угол наблюдения θ которых со стороны излучателя очень мал (рис.1), так что можно с небольшой погрешностью положить cosθ ≈ 1. Такое приближение в оптике принято называть параксиальным приближением. 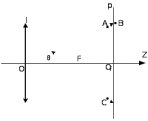 Рисунок 1 – К пояснению погрешности дифракционных формул. В теории антенн показано, что в дальней зоне поле излучения соответствует преобразованию Фурье возбуждающего поля только в точках на поверхности сфе - ры, центр которой совпадает с излучателем, и которая касается плоскости наблюдения в точке, лежащей на оптической оси (рис. 1). При переходе к оптическому анализатору спектра плоскость наблюдения перемещается из дальней зоны в частотную плоскость pанализатора (рис. 1) с сохранением пространственной структуры поля при соответствующем изменении масштаба по координатным осям в частотной плоскости. При этом упомянутая выше сфера также сжимается, и её радиус становится равным фокусному расстояниюFлинзы. На рисунке 4 дуга АОfС является частью окружности, получающейся в сечении сферы плоскостью рисунка. На рисунке 2 представлено соотношение между графиками распределения интенсивности света, излучаемого плоской апертурой. 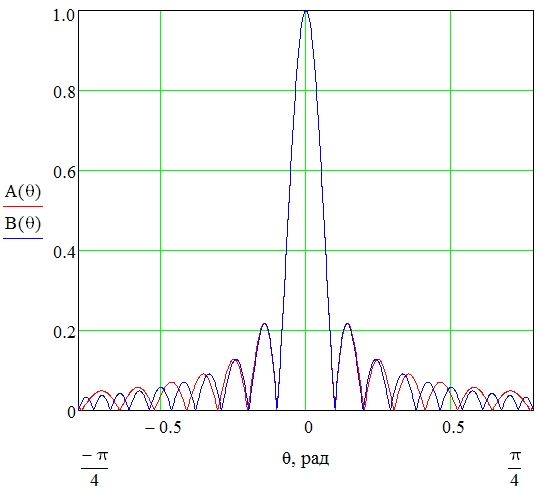 Рисунок 2 – Соотношение между графиками распределения интенсивности света, излучаемого плоской апертурой. Из сравнения графиков на рисунке 2 видно, что они достаточно хорошо совпадают только в области главного и двух первых боковых максимумов (точнее в центре спектральной картины), а далее их расхождение быстро возрастает. Это подтверждает сделанное выше замечание, что распределение интенсивности света на выходе анализатора спектра хорошо описывается пространственным преобразованием Фурье только в центральной части спектральной картины (параксиальное приближение). Расхождение графиков на рисунке 2 можно оценить функцией погрешности, которая равна относительному смещению по оси абсцисс θ соответствующих максимумов (или минимумов) на этих графиках, выраженному в процентах: 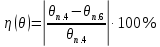 , (1) , (1) где θn.4, θn.6 – абсциссы n-го максимума (или минимума) на графиках рисунков 4 и 6 соответственно; при этом максимумы и минимумы отсчитываются от начала координат вправо (в положительном направлении оси углов θ); главному максимуму соответствует номерn = 0 и учитывается количество максимумов и минимумов, имеющееся на рисунке 6 в интервале углов 0 ≤ θ ≤ π/2. На практике сложные функции амплитудного и фазового распределения возбуждения заменяют близкими к ним, но более простыми аппроксимирующими функциями, которые существенно упрощают процедуру вычисления поля излучения в дальней зоне. Одной из таких достаточно простых функций, часто используемой для аппроксимации спадающего к краям плоской апертуры нормированного амплитудного распределения является функция «косинус на пьедестале», которая записывается в виде: 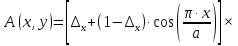 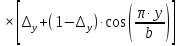 , (2) , (2)где Δxи Δy– высота «пьедестала» по координатам x и y соответственно; a, b - размеры апертуры. Параметры Δxи Δyопределяют уровень возбуждения на краю апертуры и могут изменяться в диапазоне значений от нуля до единицы. Различные виды фазового распределения возбуждающей функции можно аппроксимировать следующим выражением: 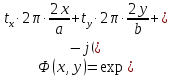 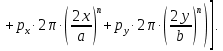 (3) (3)Выражение (3) при определённых значениях параметров tx, ty, px, py и nпозволяет задавать различные законы распределения фазы на излучающей апертуре, перечисленные в таблице 1. Таблица 1 Законы фазового распределения, реализуемые функцией Ф(x,y)
С помощью значений параметров tx, ty, px, py можно задавать максимальный сдвиг фазы на краю апертуры по соответствующей координатной оси по сравнению с её центром, управляя, таким образом, законами линейного, квадратичного и кубичного распределения фазы по апертуре. Комплексное амплитудно-фазовое распределение (АФР) возбуждения на поверхности плоской апертуры получается перемножением функций A(x, y) и Ф(x, y). Варьируя параметрами Δx, Δy, tx, ty, px, py, n, можно задавать различные амплитудно-фазовые распределения во входной плоскости (x, y) оптического анализатора спектра на основе однолинзового Фурье-процессора. В антенной технике АФР возбуждения плоской апертуры, при котором амплитуда и фаза во всех точках апертуры постоянны, принято называть неискажённым. Любые отклонения от такого распределения называются искажениями. Искажения могут быть или только амплитудные, или только фазовые, или и те, и другие одновременно. Амплитудные искажения распределения возбуждения могут носить случайный или преднамеренный характер. Случайные искажения связаны с допусками и ошибками при производстве антенн, а также с внешними воздействиями в процессе их эксплуатации. Искажения преднамеренного характера вносятся специально для достижения определённых свойств ДН антенны. Наиболее часто амплитудные искажения заключаются в уменьшении амплитуды возбуждения на краю апертуры. Фазовые искажения возбуждения антенн, как и амплитудные искажения, могут быть как случайными, связанными с особенностями производства и эксплуатации антенн, так и детерминированными вследствие особенностей конструкции антенн или преднамеренно вносимые конструкторами антенных систем при их разработке. В антенной технике наиболее часто встречаются и хорошо изучены квадратичные и кубичные нелинейные фазовые искажения. Квадратичные искажения присущи рупорным антеннам вследствие несоответствия плоской формы излучающей апертуры рупора и сферической формы фазовой поверхности излучаемой волны. В зеркальных параболических антеннах квадратичные искажения возникают из-за смещения облучателя вдоль оси параболоида из фокуса. При смещении облучателя зеркальной антенны из фокуса параболоида перпендикулярно его оси в раскрыве апертуры антенны возникают кубичные искажения. 2 Выполнение работы: Для выполнения работы вводим в программу значения, выданные преподавателем. Значения необходимые для построения диаграммы записаны в таблице 2. Таблица 2 Исходные данные
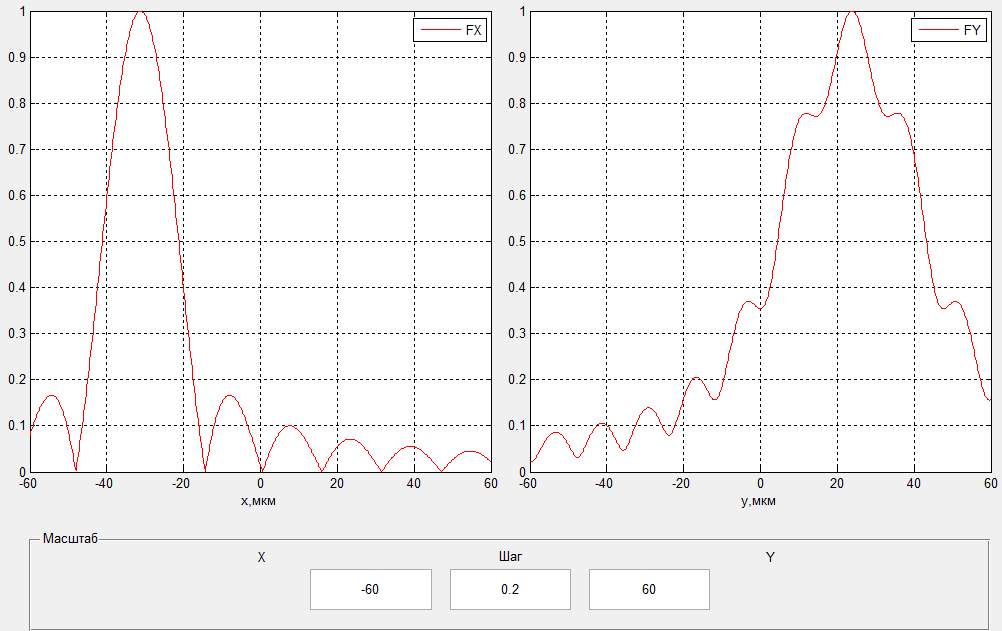 Рисунок 3- диаграмма направленности плоских апертур с неизвестными параметрами амплитудно-фазовых искажений возбуждения Первый этап работы – построение диаграммы направленности только с амплитудными искажениями. Для этого значения tx1, ty1, n, px1, py1 принимаются равными нулю, а значения Δx1, Δy1 принимаем равными 1: 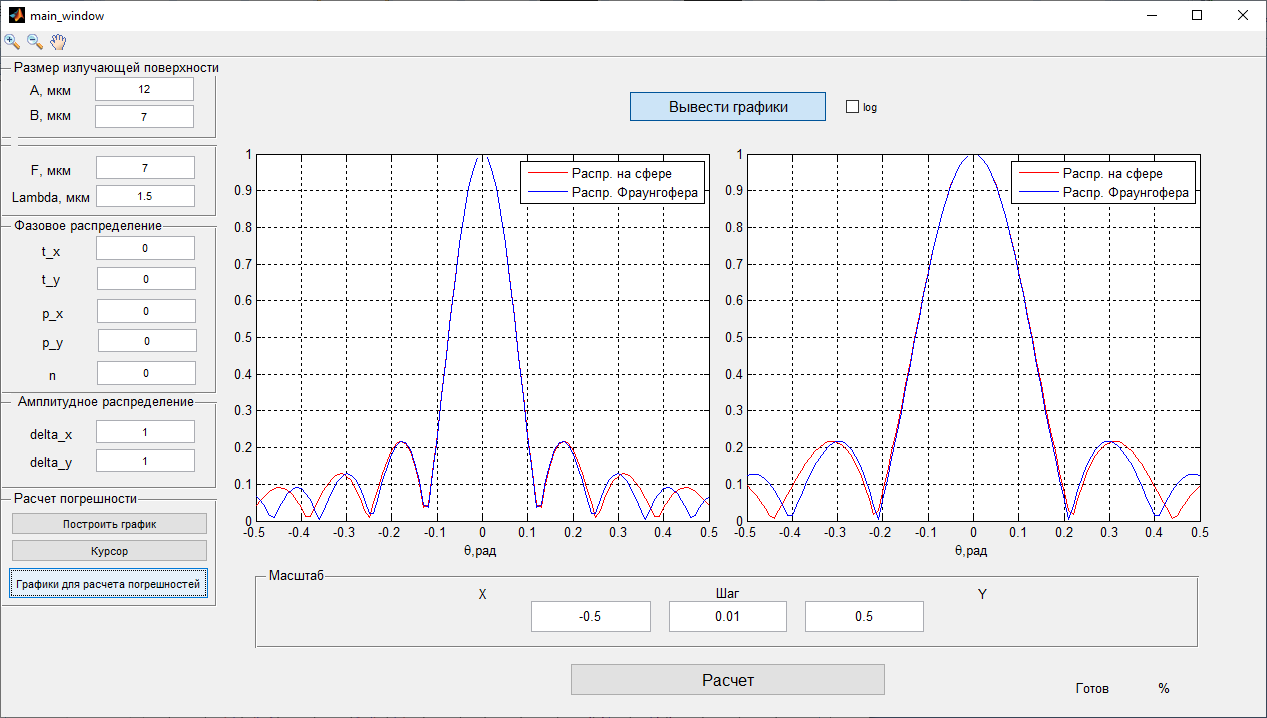 Рисунок 4 – Диаграмма направленности с амплитудными искажениями при значениях Δx1=Δy1=1 Далее по угловым координатам экстремумов этих графиков, имеющих одинаковый номер, построить графики функции погрешности в плоскостях XfZ и YfZи сравнить их между собой: 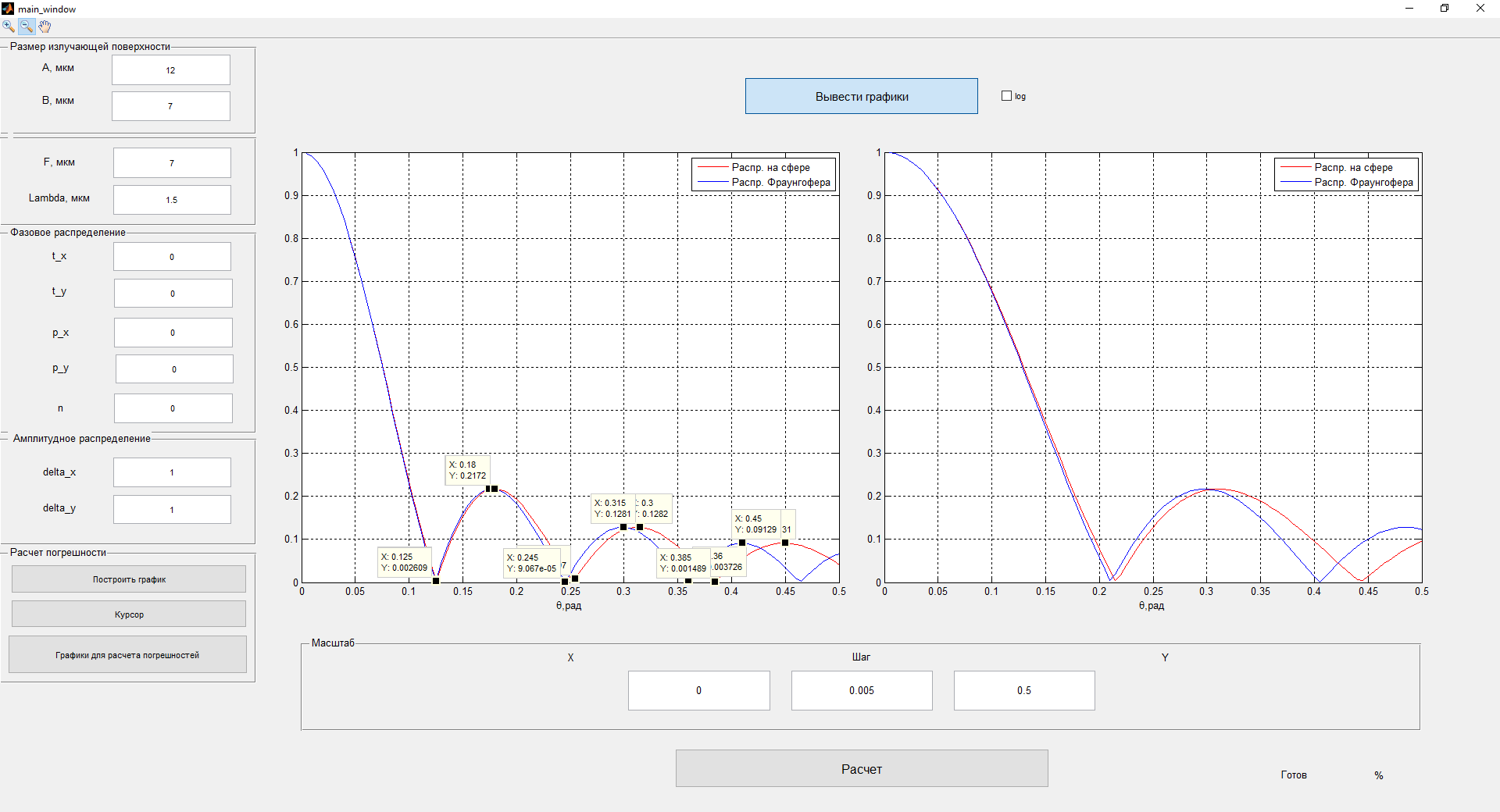 Рисунок 5 – Угловые координаты экстремумов в плоскости XfZ. 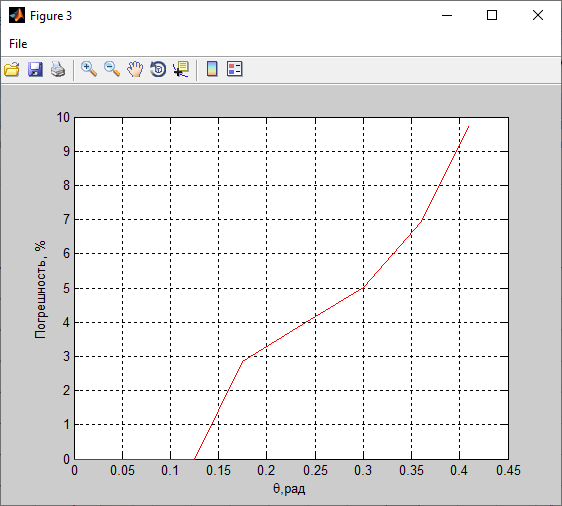 Рисунок 6 – Графики функции погрешности в плоскости XfZ. 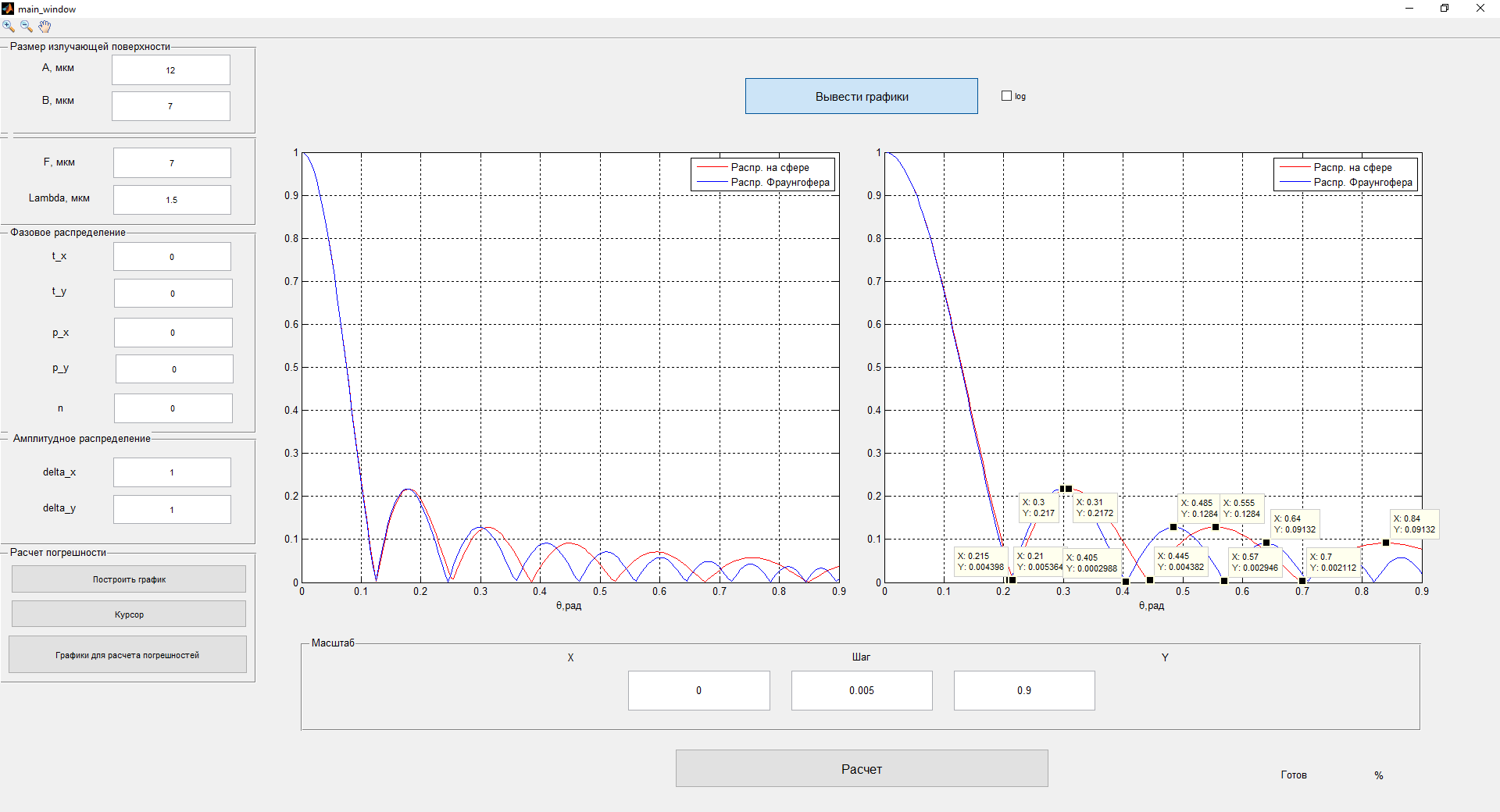 Рисунок 7 – Угловые координаты экстремумов в плоскости YfZ. 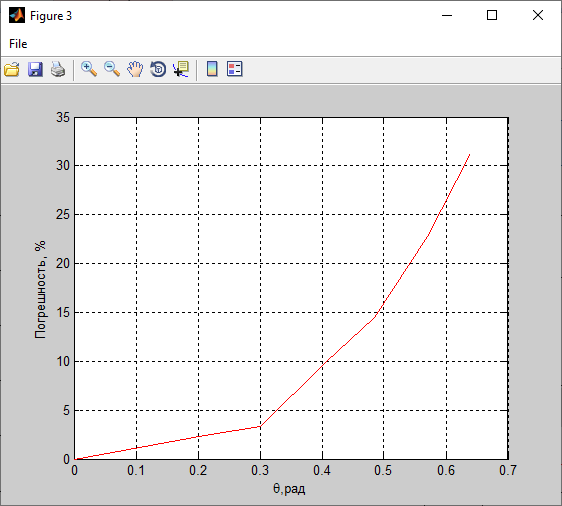 Рисунок 8 – Графики функции погрешности в плоскости YfZ. Пользуясь построенными графиками, определим в плоскостях XfZ и YfZграницы области наблюдения диаграммы направленности (в микрометрах) в частотной плоскости анализатора пространственного спектра, на которых значения функции погрешности η(θ) не превышают значения, приведенного в колонке 5 таблицы 2 для заданного варианта. Переход от угловых границ области наблюдения 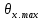 и и 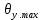 к линейным осуществляется по формулам: к линейным осуществляется по формулам: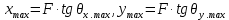 . .где F– фокусное расстояние равное 7 мкм (с учетом варианта), 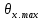 и и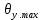 – выбираются из графиков на рисунках 5 и 7 соответственно, приблизительно равны 0,38 рад. – выбираются из графиков на рисунках 5 и 7 соответственно, приблизительно равны 0,38 рад.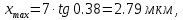 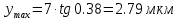 . .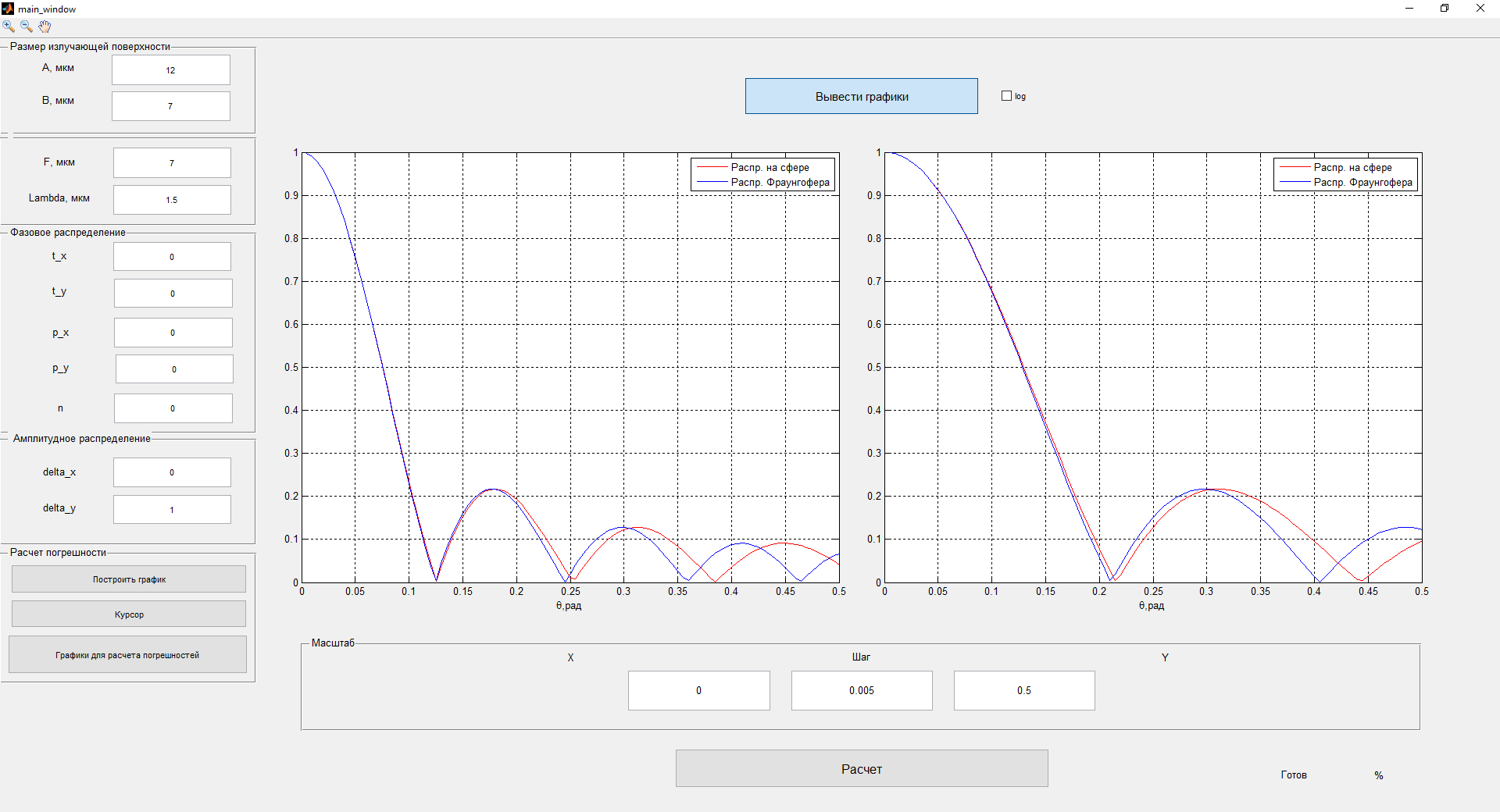 Рисунок 9 – Диаграммы направленности при амплитудных искажениях. 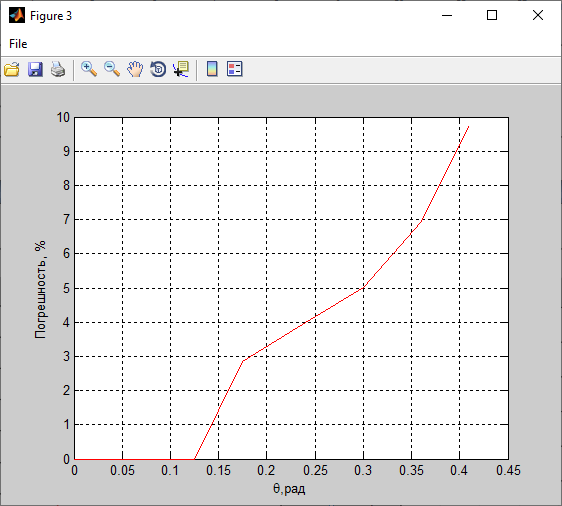 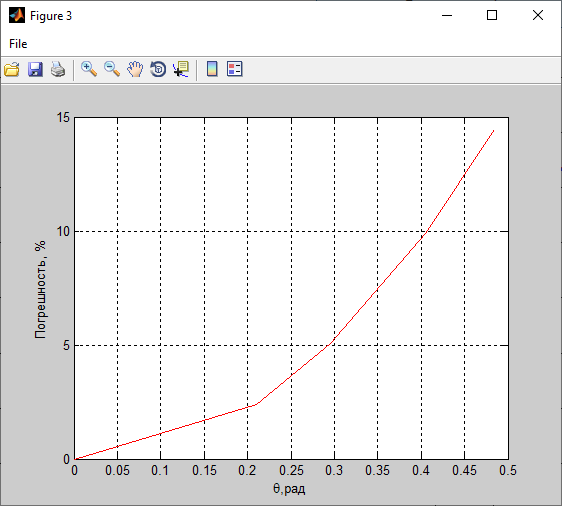 Рисунок 10 – Графики функции погрешности при амплитудных искажениях. 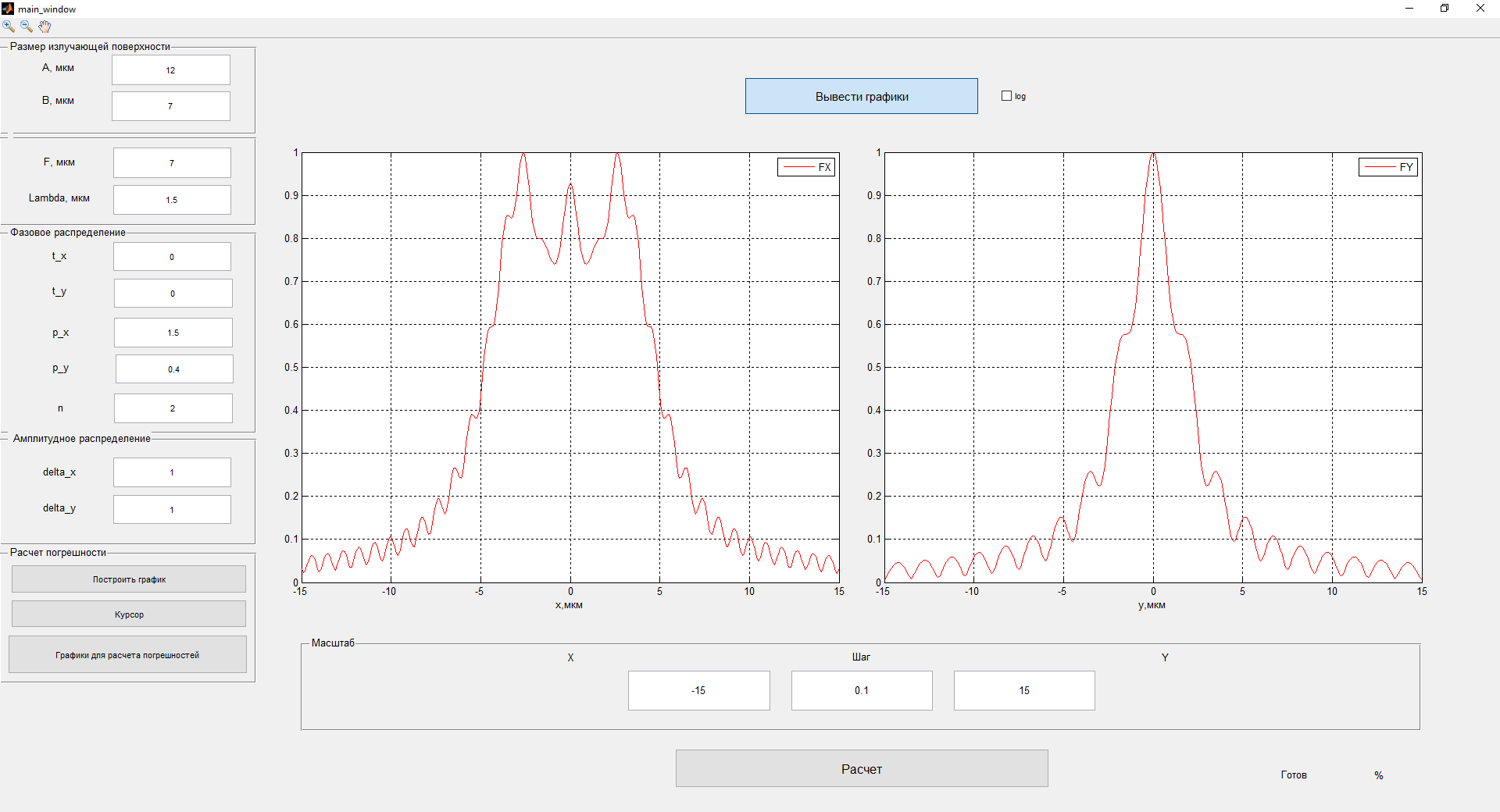 Рисунок 11 – Диаграммы направленности при первом наборе фазовых искажений. 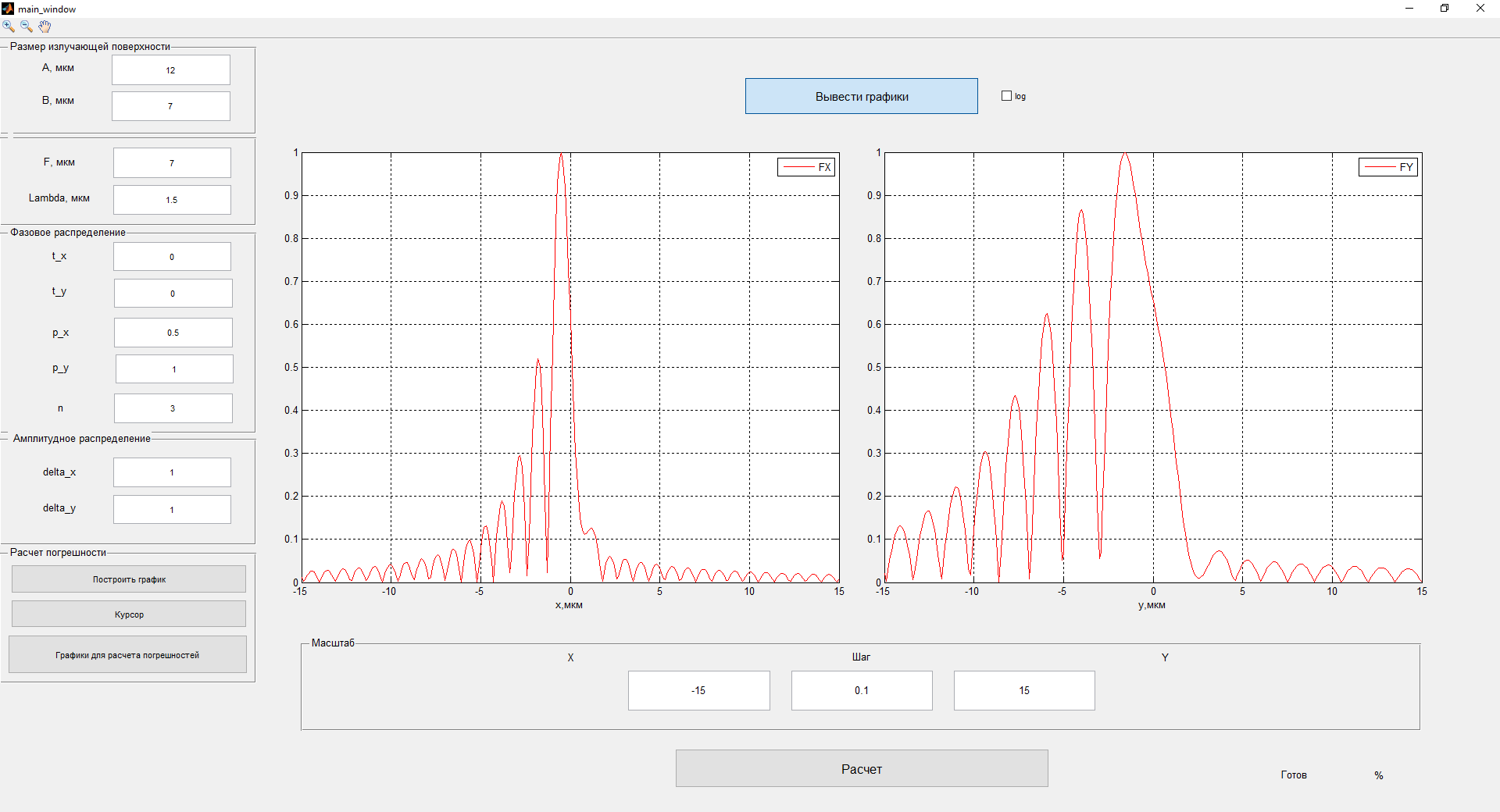 Рисунок 12– Диаграммы направленности при втором наборе фазовых искажений. Делаем вывод, что с ростом значений px1, py1 увеличивается ширина главного лепестка, при этом первые боковые максимумы плохо различимы, уменьшение значений Δx1, Δy1 приводит к росту значений ширины главного лепестка, но при этом уменьшаются значения амплитуд боковых лепестков. При значении n=3 диаграмма направленности перестает быть симметричной. 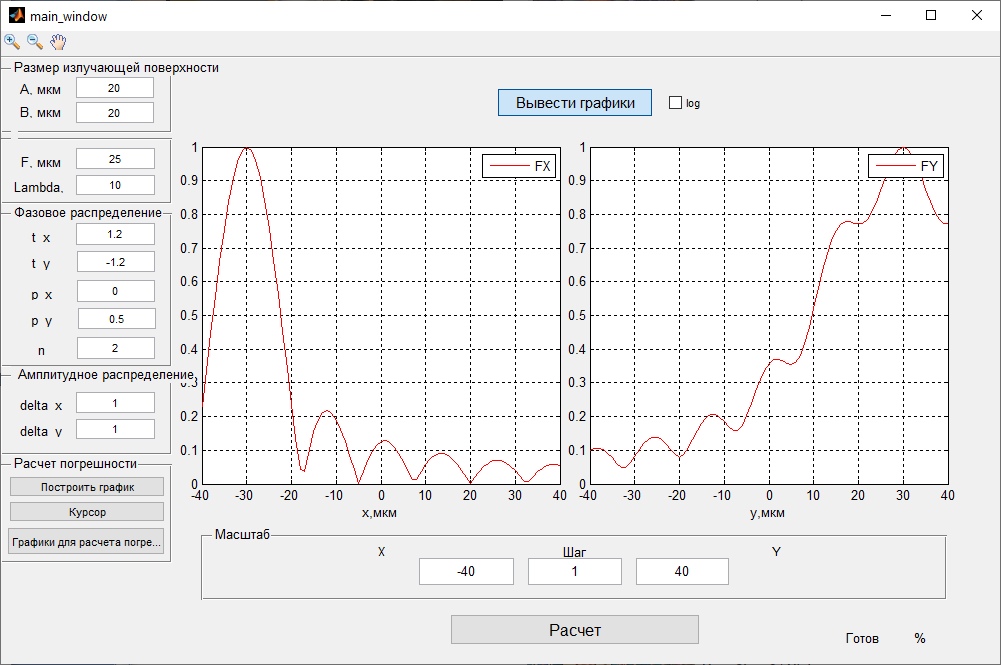 Рисунок 13- диаграмма направленности плоских апертур с известными параметрами амплитудно-фазовых искажений возбуждения На основе полученного графика делаем вывод, что есть линейные фазовые искажения, т.к. графики сдвинуты по оси X, и квадратичные фазовые искажения на графике FY, с коэффициентом <1 Кальченко А.А Окорочков А.И Провер. Листов Дата Подпись № докум. Лист Изм Лист Лит Разраб. Н.контр. Утв. ИСОиП(филиал)ДГТУ кафедра «РЭСиК» | |||||||||||||||||||||||||||||||||||||||||||||||||||
