Лабораторная работа № 1. «Математические модели линейных стационарных систем управления». ЛР 1 МХТ 14. Лабораторная работа Математические модели линейных стационарных систем управления
 Скачать 1.73 Mb. Скачать 1.73 Mb.
|
|
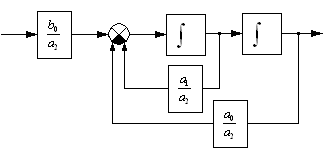
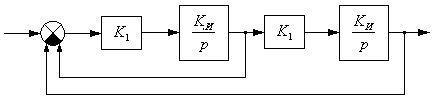
Лабораторная работа № 1. «Математические модели линейных стационарных систем управления» Цель работы:изучить способы математического описания линейных систем управления, освоить основные приёмы моделирования систем управления в среде Simulink. Приборы и оборудование: - Компьютер совместимый с IBM PC,128-512 Мб. ОЗУ; - Операционная система WINDOWS NT, XP, UNIX; - Математический пакет MATLAB Version 7.*. Форма отчётности студентов: индивидуальный отчёт с типовым титульным листом и результатами моделирования. Длительность работы: 4 академических часа. Защита работы: собеседование с преподавателем по контрольным вопросам, выполнение индивидуальных заданий. I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Динамическая система – это весьма широкое понятие, которое охватывает разнообразные физические процессы, протекающие во времени и пространстве. Характер подобного процесса, его закон описывается некоторой системой дифференциальных уравнений (ДУ). Система дифференциальных уравнений, описывающая некоторый пространственно-временной процесс, представляет собой математическую модель динамической системы. Большой класс динамических систем описывается линейными дифференциальными уравнениями. Математические модели непрерывных линейных систем. Классический метод исследования линейных непрерывных систем основан на составлении и последующем решении дифференциальных уравнений, связывающих координаты системы с поступающими воздействиями. Для составления математической модели системы необходимо разбить её на звенья направленного действия. Это звено может являться техническим устройством любой физической природы, конструкции и назначения. Для получения общего уравнения системы рассматривают каждое звено в отдельности и составляют для него уравнения, связывающие вход и выход. Уравнение динамики каждого отдельного звена является предметом соответствующей научной дисциплины (динамика, механика, электротехника, теплофизика, химия и т.д.). Деление системы на отдельные звенья позволяет рассматривать выходной сигнал одного звена в качестве входного для последующего. Дифференциальное уравнение – это первая форма записи математической модели системы. Для качественного анализа широко используются модели линейных систем в форме оператора связи между входом и выходом системы, что позволяет ввести вторую форму записи - передаточную функцию, которая позволяет решить дифференциальное уравнение алгебраически. Математическая модель одной и той же системы может быть различной в зависимости от цели исследования. Математическая модель, с одной стороны, должна как можно полнее отражать свойства оригинала, с другой стороны, быть по возможности простой. Математическое описание систем с помощью ДУ. Рассмотрим детерминированную непрерывную стационарную динамическую систему, состоящую из звеньев, описываемых линейными диф. уравнениями с постоянными коэффициентами. 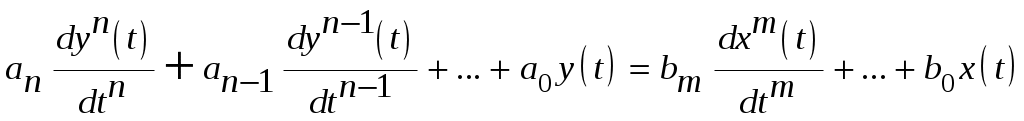 , (1) , (1)Где Число 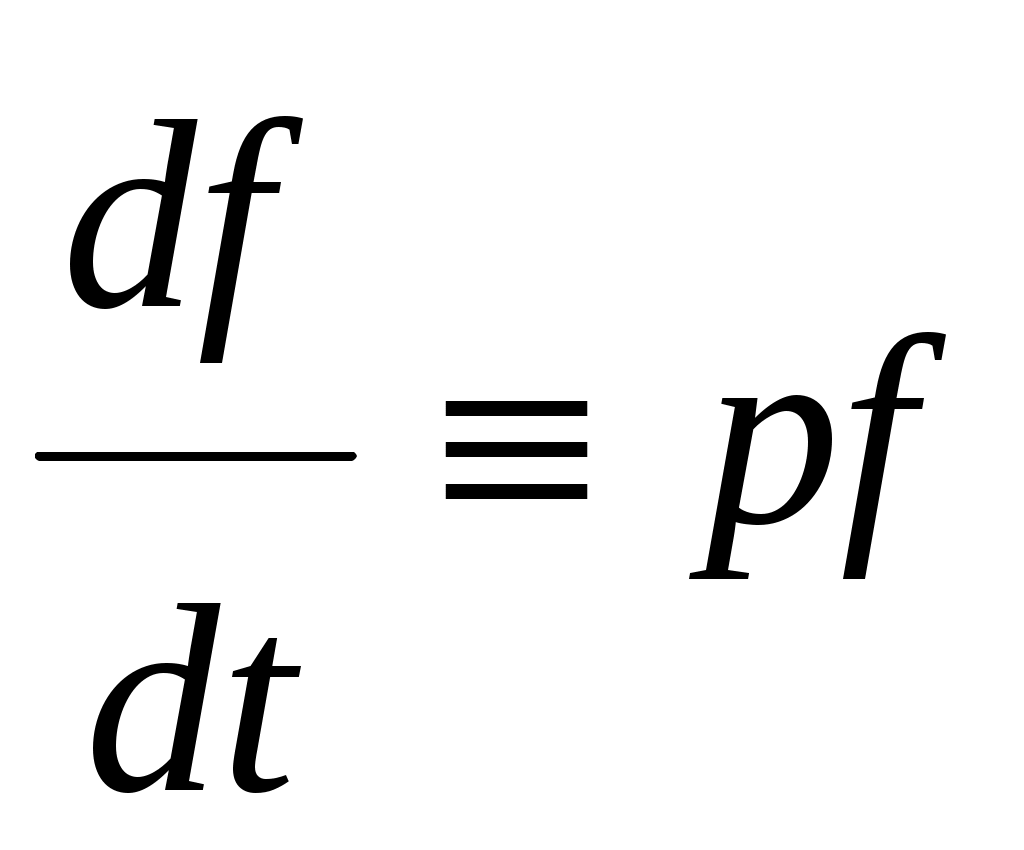 или или 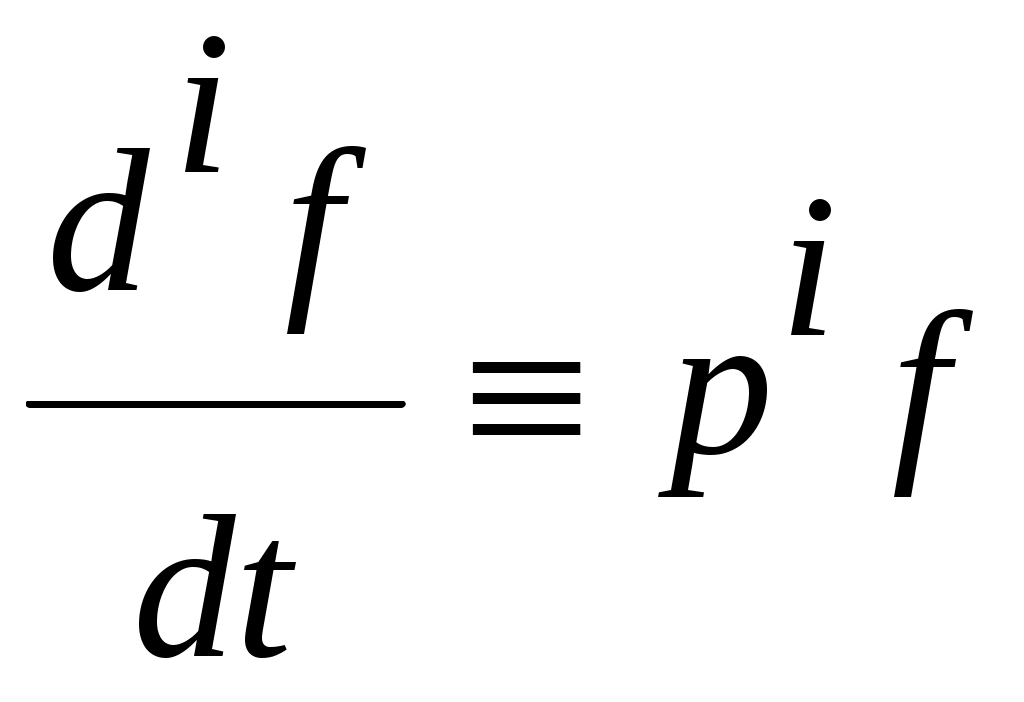 , тогда уравнение (1)запишется в виде: , тогда уравнение (1)запишется в виде:При записи и преобразовании ДУ оператор дифференцирования нужно рассматривать как алгебраический сомножитель, а выражение Учитывая это замечание, вынесем Т.о., мы перешли к форме записи ДУ, которая называется операторной или символической. Линейные ДУ с постоянными коэффициентами записывают в теории управления в стандартной форме. При этом члены, содержащие выходную величину и её производные, записываются в левой части уравнения, а все остальные в правой. В правой части члены, содержащие входную величину и её производные, объединяют в одну группу и коэффициент выносят за скобки. Коэффициенты при выходной и входной величине делают равным 1. Введём обозначения: Это постоянные времени, которые характеризуют инерционные свойства системы. Окончательно получаем уравнение (1) в стандартной форме: Операторная передаточная функция Вернёмся к уравнению (3) и введём обозначения: Тогда уравнение (3) можно записать в компактной форме: Оператор Назовём отношение оператора воздействия к собственному оператору операторной передаточной функцией и будем обозначать Уравнение (7) представляет вторую форму записи ДУ. Замечание. Приведённые выше записи являются символическими, поскольку не дают решения исходного ДУ относительно выходной величины, т.к. не определена операция деления оператора на оператор. Решить эту задачу позволяют правила операционного исчисления, основанные на преобразованиях Лапласа. II. ПРАКТИЧЕСКАЯ ЧАСТЬ Объектом исследования в данной лабораторной работе являются аналитические формы представления динамических процессов, а целью – получение структурных математических моделей типовых линейных звеньев. Модели линейных систем могут быть представлены аналитически в виде: дифференциального уравнения n-го порядка; системы n дифференциальных уравнений первого порядка; передаточной функции, записанной в общем виде; передаточной функции как соединении типовых передаточных функций элементарных звеньев. Линейное дифференциальное уравнение вида (1) и (2) запишем в виде где |

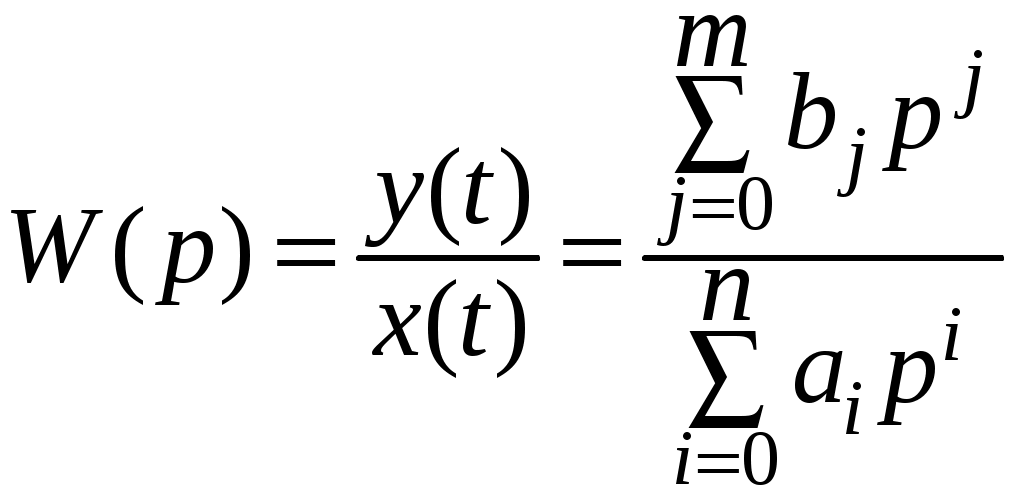
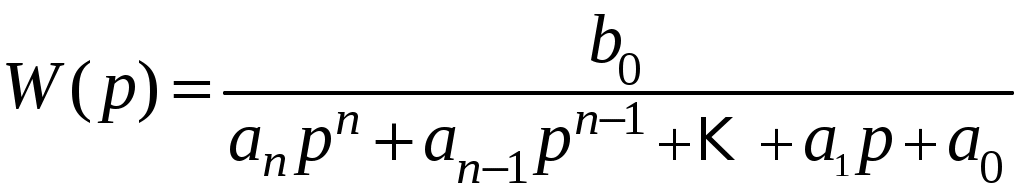
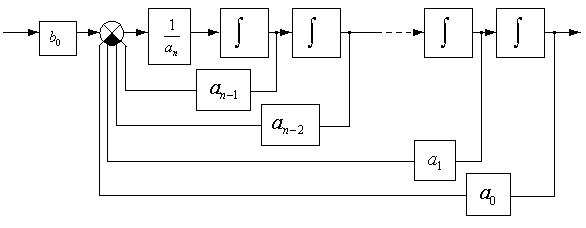
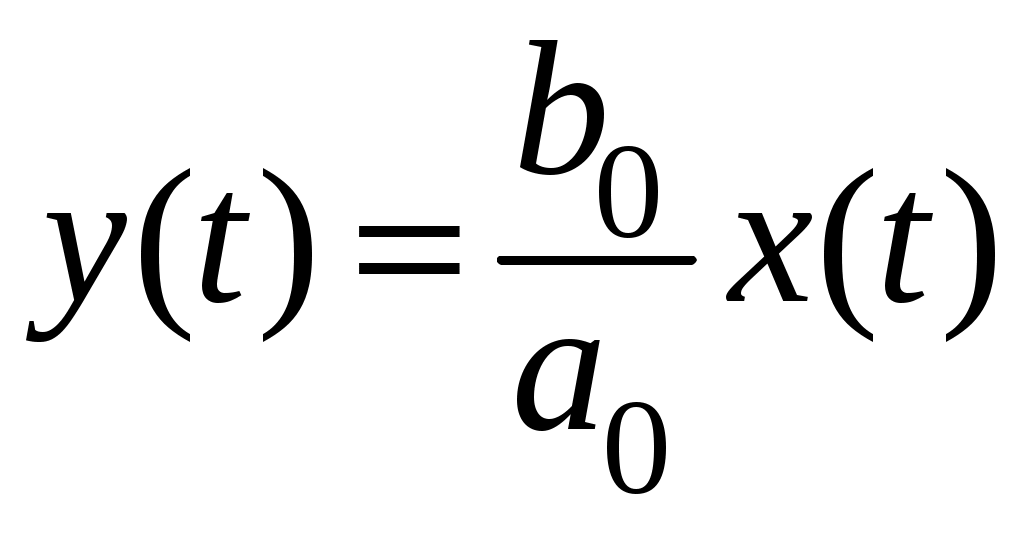 .
. 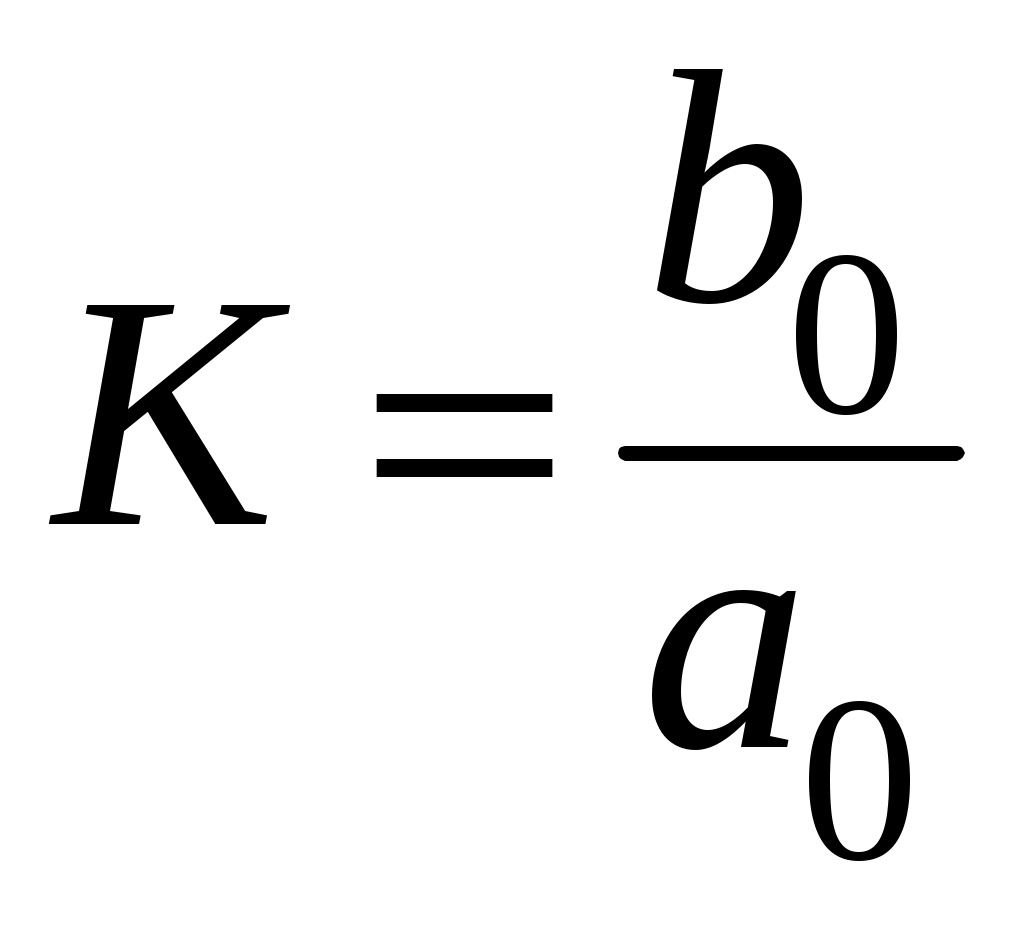 , где К – коэффициент усиления. Передаточная функция системы будет иметь вид
, где К – коэффициент усиления. Передаточная функция системы будет иметь вид 
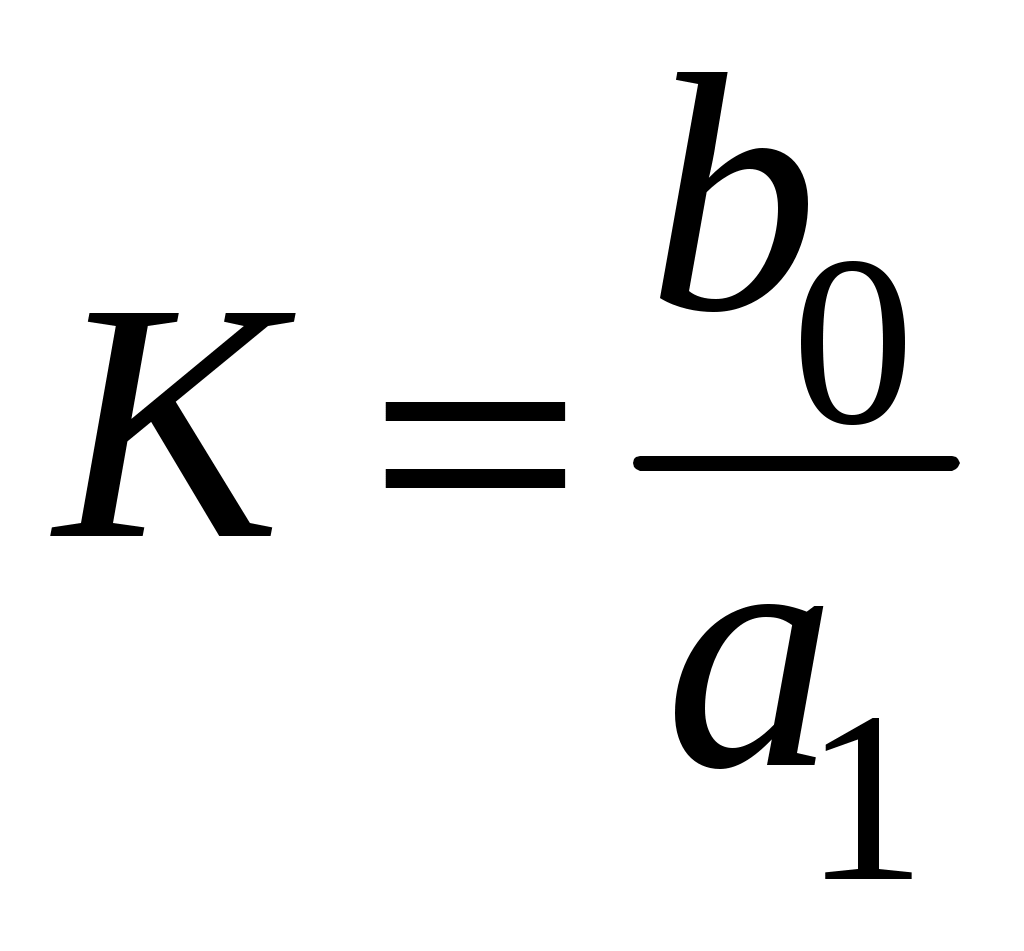 , тогда передаточная функция имеет вид:
, тогда передаточная функция имеет вид: 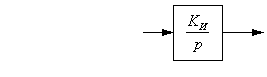
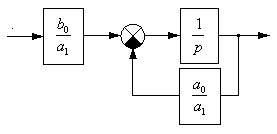
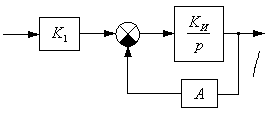
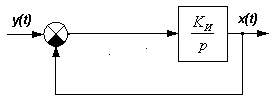
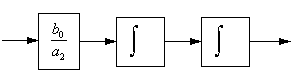
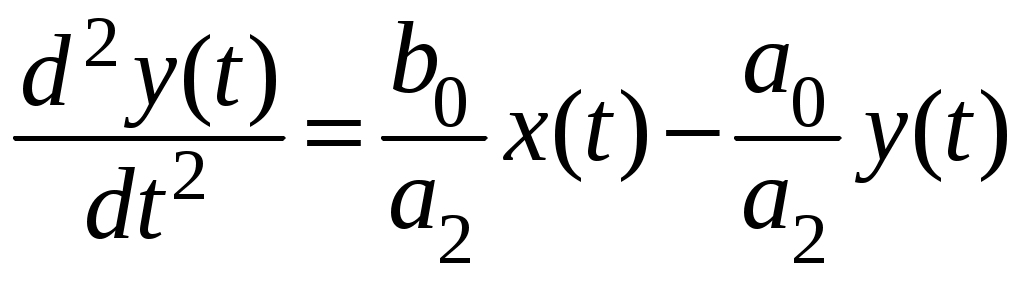 .
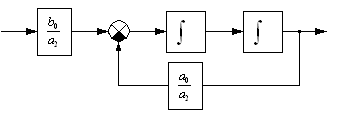
.
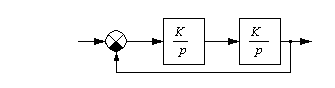
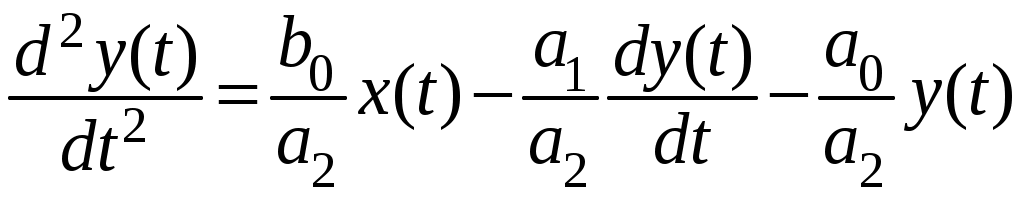 .
.