ответы на вопросы. ответы на билеты тау. Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
|
Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем. В теории управления при анализе и синтезе систем управления имеют дело с их математической моделью. Математическая модель САУ представляет собой уравнения, передаточные или временные(ударение на предпоследнем слоге)функции, которые описывают процессы, протекающие в системе управления. Математическая модель может быть получена аналитически на основе физических законов, которым подчиняются процессы в системе управления, или экспериментально. При математическом описании исходят из противоречивых требований. С одной стороны, математическая модель должна как можно полнее отражать свойства оригинала (исходной системы), а с другой стороны –быть по возможности простой, чтобы не усложнять исследование. Часто полезно на начальном этапе исследования принимать более простую модель, а затем при необходимости усложнять ее, принимая во внимание дополнительные факторы, которые на начальном этапе не учитывались. Под идентификацией (математическим описанием) объекта понимается построение символической модели, устанавливающей закономерность между выходными и входными переменными объекта, которая дает возможность определить с заданной точностью выходную переменную объекта — оригинала по ее входным переменным. Основным методом построения математической модели объекта управления является статистический, т. е. метод, основанный на статистической динамике систем автоматического управления. При проектировании и исследовании САУ необходимо знать уравнения, описывающие их движения. Процессы в САУ описываются дифференциальными, разностными, интегральными и интегро-дифференциальными уравнениями, которые называют ее математической моделью. При исследовании САУ на различных этапах математическая модель может быть различной. Начинают исследования САУ с простейшей математической моделью, а затем ее усложняют, учитывая дополнительные связи и влияния. Такой подход объясняется тем, что к математической модели предъявляются противоречивые требования. Математическая модель должна достаточно полно описывать динамику САУ и при этом быть по возможности простой. В дальнейшем будут рассматриваться только обыкновенные дифференциальные уравнения, в неявной форме которые могут быть записаны или
Уравнения (3.1) и (3.2) могут быть записаны в явной форме, разрешенные относительно старшей производной (например, (3.2)) Данное дифференциальное уравнение в явной форме n-го порядка можно преобразовать в систему n дифференциальных уравнений первого порядка: 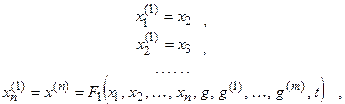 путем введения новых неизвестных Если в дифференциальное уравнение (3.2) входит n неизвестных функций , тогда можно записать систему из n уравнений первого порядка в виде где В векторной форме дифференциальное уравнение будет иметь вид или ,
Широкое применение в ТАУ получила операторная форма записи дифференциального уравнения. Это объясняется тем, что от дифференциального уравнения посредством интегрального преобразования (например, преобразования Лапласа) переходят к операторной форме. Операторное уравнение является алгебраическим и его решение проще, чем дифференциальное. Затем из полученного решения операторного уравнения с помощью обратного преобразования получают решение дифференциального уравнения. Дифференциальное уравнение (3.1) при нулевых начальных условиях в операторной форме можно записать или где 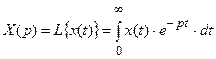 - преобразование Лапласа от ; - преобразование Лапласа от ;- параметр преобразования Лапласа. Операторная форма записи дифференциального уравнения, когда начальные условия по всем переменным равны нулю, совпадает с символической формой, когда 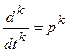 , а p – символ дифференцирования. Поэтому для получения операторной формы записи дифференциального уравнения, когда начальные условия нулевые, применяют приемы символической формы. , а p – символ дифференцирования. Поэтому для получения операторной формы записи дифференциального уравнения, когда начальные условия нулевые, применяют приемы символической формы.Уравнение движения САУ в любой форме полностью описывает весь процесс управления, т.е. процесс изменения управляемых величин как в переходном, так и в установившемся режимах. Под установившимся режимом понимают процесс, при котором регулируемая (управляемая) величина изменяется по закону, определяемому лишь законом изменения задающего воздействия. Установившейся режим САУ, относительно которого рассматривается движение системы в процессе управления, называется исходным. Переходным режимом называется изменение управляемой величины при переходе САУ из одного в другое установившееся состояние. Если в установившемся режиме воздействия после их приложения больше не изменяют своих величин во времени, то в САУ устанавливается так называемый статический режим. Уравнение статики может быть получено из уравнения движения САУ (3.1), если все члены, содержащие производные, приравнять нулю, то есть или , где - коэффициент передачи САУ. Графическое отображение данной зависимости, т.е. зависимости между выходной x и входной g величинами САУ в статическом режиме, называется статической характеристикой (рис. 3.1).
Рис.3.1. Статические характеристики элементов САУ Статические характеристики элементов САУ и систем в целом могут быть как линейными (кривая 1, рис. 3.1), так и нелинейными (кривая 2, рис. 3.1). Если характеристика нелинейная, то необходимо учитывать влияние данной нелинейности на динамику САУ. Операторы преобразования переменных. Классы моделей. Рассмотрение причинно-следственного взаимодействия системы управления со средой связано с обособлением собственно системы S и выделением ее связей со средой через переменные входа f и выхода у (рис.1). Система оказывается звеном в искусственно разорванной цепи причинно-следственных отношений «среда – система – среда». На содержательном уровне объекты и системы управления интерпретируются как устройства получения, передачи и обработки информации. С другой стороны, объекты и системы можно рассматривать как преобразователи сигналов – носителей этой информации. Преобразование сводится к изменению параметров, кодирующих информацию. Свойства системы как преобразователя характеризуются ее оператором, отображающим множество функций времени на входе системы на множество функций выхода:  Оператор линеен, если обладает свойствами однородности и аддитивности, т. е. 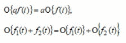 В общем случае линейной комбинации входных воздействий отвечает та же линейная комбинация соответствующих реакций: 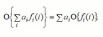 Свойство линейности оператора, выраженное приведенной формулой, иногда называют принципом суперпозиции. Принцип суперпозиции дает возможность выражать реакцию линейной системы на любое воздействие через ее реакцию на определенный вид элементарных воздействий fi(t). При построении моделей стремятся к их простоте при максимальной адекватности оригиналам. В частности, принимают гипотезу о линейности оператора, что принципиально упрощает анализ и синтез. Если принцип суперпозиции не выполняется, то оператор называется нелинейным. Разумеется, класс нелинейных операторов много богаче класса линейных. Оператор стационарен, если его характеристики инвариантны ко времени. Другими словами, при сдвиге во времени входного воздействия без изменения его формы реакция претерпевает такой же сдвиг во времени без изменения своей формы. В ряде случаев модели должны отражать изменение свойств объекта во времени, тогда вводятся в рассмотрение нестационарные операторы  Нестационарность оператора учитывает воздействие среды принципиально иного характера, чем сигнальный вход f(t). В простейшем случае нестационарность сводится к изменению параметров модели, например коэффициентов дифференциального уравнения. В общем случае влияние среды приводит к необходимости изменения структуры оператора, например порядка дифференциального уравнения. Если вариации оператора происходят много медленнее основных процессов, то вместо нестационарного оператора рассматривают множество стационарных операторов, различающихся значениями параметров. Описание объекта множеством равновероятных операторов содержит неопределенность. Если параметры модели заданы с точностью до интервалов значений, то о таких системах говорят, что они интервальные. Оператор может быть детерминированным или стохастичным. В случае стохастичных операторов параметры представляются как случайные величины и задаются их вероятностные характеристики. Объекты управления могут быть с сосредоточенными или распределенными параметрами. В последнем случае они описываются уравнениями в частных производных (разностях). Модель объекта или системы управления принадлежит тому же классу, что и описывающий их оператор преобразования. Выделяют следующие признаки классов систем с непрерывным и дискретным временем: • линейные Л или нелинейные Л; • стационарные С или нестационарные С; • детерминированные Д или стохастичные Д; • сосредоточенные (конечномерные) К или распределенные (бесконечномерные) К. Эти четыре независимых признака биальтернативны, поэтому можно насчитать всего 24 = 16 классов непрерывных и столько же дискретных систем. Простейший класс – ЛСДК – линейные стационарные детерминированные конечномерные системы. Они имеют форму обыкновенных линейных дифференциальных (разностных) уравнений с постоянными детерминированными коэффициентами. Математика разработала весьма развитый аппарат анализа этого класса систем. Более сложные классы операторов получаются при введении одного из альтернативных признаков: ЛСДК; ЛСДК; ЛСДК; ЛСДК. Для таких систем существует незначительное число общих методов аналитического исследования, разработанных только для частных случаев. Операторы второго уровня сложности получаются введением двух отрицаний: ЛСДК; ЛСДК; ЛСДК; ЛСДК; ЛСДК; ЛСДК. При трех отрицаниях получаем операторы третьего уровня сложности: ЛСДК; ЛСДК; ЛСДК; ЛСДК. Операторы четвертого уровня сложности – ЛСДК – нелинейные нестационарные стохастичные бесконечномерные. Им соответствуют нелинейные дифференциальные уравнения в частных производных с переменными случайными параметрами. Для систем, описываемых операторами второго и выше уровней сложности, имеется, как правило, только единственная возможность их анализа и синтеза путем вычислительных экспериментов. Если модель системы образована элементами различных классов, то класс системы определяется классом элемента с максимальным числом отрицаний. Система называется автономной, если на нее не действуют внешние силы, в том числе параметрического типа. Автономные системы, таким образом, стационарны. Изменение их состояния происходит в силу накопленной ранее энергии. На рис.2 модель среды представлена в виде автономной системы, имеющей выходы, но не имеющей входов. Движения автономной системы называют свободными. Дифференциальные уравнения автономных систем включают переменные системы и их производные, но не содержат переменных, описывающих воздействия среды, и имеют постоянные параметры. Это так называемые однородные дифференциальные уравнения 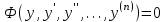 , ,дополняемые начальными условиями 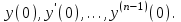 Начальные условия являются следствием предыстории системы и вместе с дифференциальными уравнениями полностью определяют поведение автономной системы. В случае автономных систем с дискретным временем будем иметь однородные разностные уравнения: 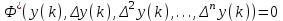 . .Среда на входе системы моделируется автономными системами – генераторами воздействий или преобразователями типовых воздействий – фильтрами. Распространенными типовыми сигналами, моделирующими детерминированное воздействие, являются единичные импульсная и ступенчатая функции. Примером типового случайного воздействия является так называемый «белый шум». Среда может моделироваться динамической системой того же класса, что и сама система управления. Однако часто рассматриваются детерминированные системы со случайными воздействиями на входе. Модели вход-выход. Дифференциальные уравнения, передаточные функции. Простейшая модель системы называется моделью входа-выхода. Она включает в себя блоки входов, выходов и процесса преобразования, который иногда называют «черным ящиком».  Так, система обучения студента с использованием дистанционной технологии посредством данной модели может быть изображена следующим образом. 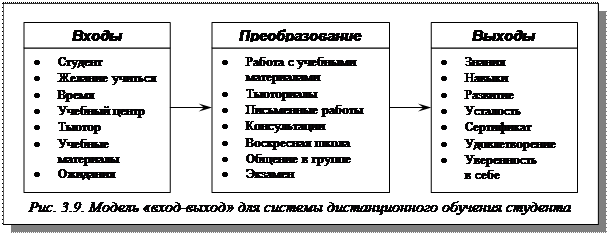 Несмотря на простоту этой модели, она вооружает нас эффективным инструментом анализа функционирования всей системы. Например, если во входах системы (рис. 3.9) будет отсутствовать «желание учиться», то для получения тех же выходов нам необходимо будет радикально изменить само преобразование и ввести подсистему мотивации. Обычно в данном типе схем каждый фактор на входах и выходах пишется над отдельной стрелкой. Но при построении схем с помощью компьютера это довольно неудобно и, если не стоит задача показать источник конкретного входа или дальнейший путь выхода, то лишние стрелки можно опустить. При исследовании и расчете САУ исходят из математического описания, происходящих в них процессах. Для линейных САУ широко используется для этой цели операторный метод. Его сущность в том, что исследуемая система разделяется на звенья направленного действия. Совокупность этих звеньев совместно с линиями связи между ними, характеризующими их взаимодействие, образуют структурную схему САР. Они отражают математически динамические свойства системы. Разбиение системы на звенья существенно облегчает их расчет. Процессы, протекающие в САУ, описываются дифференциальными. уравнениями. Задача составления дифференциальных уравнений системы сводится к составлении системы отдельных звеньев. Любое звено автоматической системы предназначено для измерения, усиления или какого-либо другого преобразования сигнала. В связи с этим для любого элемента характерной являются связи между его входным и выходным сигналом. Именно эта связь и может быть представлена дифференциальными уравнением, которое математически выражает физические процессы в звене, т. е. процессы формирования выходного сигнала элемента, при подаче на его вход входного сигнала. Для облегчения исследования сложных систем дифференциальных уравнений, описывающие поведение системы заменяются алгебраическими, с помощью преобразований Лапласа. Если имеется некоторая функция f(t) независимой вещественной переменной t, то преобразование Лапласа, производимое над этой функцией и обращающее ее в функцию F(x), определяются след соотношением 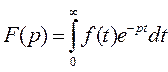 где p-произвольная комплексная величина, имеющая вещественную и мнимую часть. При этом функция f(t) называется оригиналом, а F(p)-изображением функции. Сокращенно преобразования Лапласа обозначаются: Для линейных звеньев связь между входным и выходным сигналом может быть описана линейным дифференциальным уравнением следующего вида: (1) Воспользовавшись преобразованием Лапласа, дифференциальным уравнением (1) может быть представлено в следующем виде: 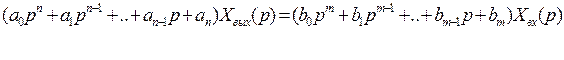 (2) Левая часть равенства в скобках - выходной операторный полином, правая – входной. Передаточной функцией звена или системы автоматического управления называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины. 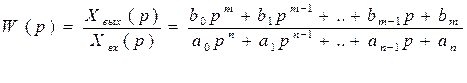 1) При р=0 выражение передаточной функции превращается в коэффициент усиления. W(p)=K. 2) Из выражения передаточной функции видно, что изображение выходной величины равно: Этим выражением можно пользоваться при определении характера переходных процессов, возникающих в системе, при подаче на ее вход любого произвольно меняющегося входного воздействия. Анализ и синтез систем автоматического управления предполагает предварительное получение информации о виде передаточной функции. Для ряда типовых динамических звеньев передаточные функции являются одинаковыми, отличие может состоять в коэффициенте выражений передаточных функций. |

