ответы на вопросы. ответы на билеты тау. Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
|
Переходная функция системы (звена). Переходная характеристика. Методы расчета и построения переходной характеристики. Эта динамическая характеристика используется для описания одноканальных объектов (2.5) с нулевыми начальными условиями Переходной характеристикой (переходной функцией) h(t) называется реакция системы на единичное ступенчатое входное воздействие u(t) = 1(0 при нулевых начальных условиях. 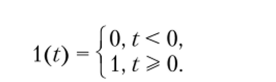 Отметим, что единичная ступенчатая функция — это функция, которая обладает свойством На рис. 2.4 приведен пример переходной характеристики системы. 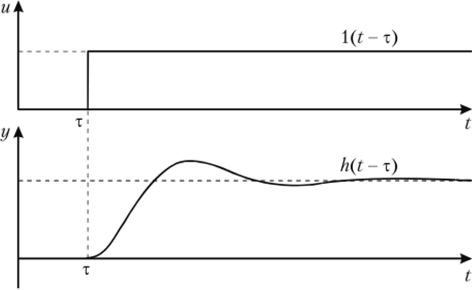 Рис. 2.4. Пример переходной характеристики системы: х — момент возникновения входного воздействия Для аналитического определения переходной функции следует решить дифференциальное уравнение при нулевых начальных условиях и единичном входном воздействии. При исследовании реального объекта переходную характеристику можно получить экспериментальным путем, подавая на его вход ступенчатое воздействие и фиксируя реакцию на выходе. Если входное воздействие представляет собой неединичную ступенчатую функцию u(t) = k 1(?), то выходная величина будет равна y(t) = kh(t), т.е. представляет собой переходную характеристику с коэффициентом пропорциональности k. Зная переходную характеристику, можно вычислить реакцию системы на произвольное входное воздействие с помощью интеграла свертки где т — переменная интегрирования. Изображение переходной функции имеет вид . Оригинал переходной функции может быть получен использованием точных и приближенных методов. Будем рассматривать только точные методы, связанные с применением обратного преобразования Лапласа. Построение переходной функции при использовании таблиц преобразования Лапласа начинается с представления ее изображения в виде произведения передаточных функций типовых звеньев. 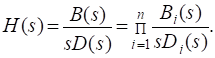 Затем это выражение преобразуется в сумму передаточных функций с неопределенными коэффициентами 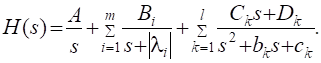 (4) В этом выражении A, Bi, Ck, Dk - неопределенные коэффициенты, i - вещественные корни уравнения D(s)=0, а выражения s2+bks+ck -соответствуют комплексно - сопряженным корням характеристического уравнения. Выражение (4) необходимо привести к общему знаменателю и числитель полученного выражения приравнять числителю изображения исходной переходной функции B(s). Приравнивая члены при одинаковых степенях опрератора s в левой и правой частях, получим систему уравнений относительно неопределенных коэффициентов. Вычислив значения этих коэффициентов, обратимся к таблицам преобразования Лапласа и определим оригиналы слагаемых формулы (4). Отметим, что оригиналы, соответствующие первым двум членам суммы (4), определяются непосредственно из таблиц, определение оригиналов для третьего члена этой суммы могут потребоваться некоторые преобразования. Оригинал переходной функции может быть получен использованием формулы обратного преобразования Лапласа, так называемой формулы разложения. В общем случае формула разложения имеет вид 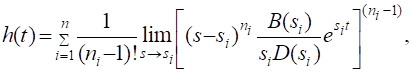 (5) где si - корни уравнения sD(s)=0, ni- кратность корней. В случае только простых корней, когда среди них имеются m вещественных корней и l пар комплексно - сопряженных корней, формула разложения принимает вид 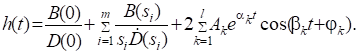 (6) В этом выражении k и k - вещественная и мнимая части комплексно сопряженных корней, а Амплитуда фаза колебательных составляющих определяются следующим образом: 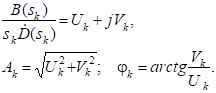 При вычислениях по этим формулам, в первую подставляется только один из пары комплексно - сопряженных корней. При вычислении фазового сдвига необходимо учитывать квадрант, в котором находиться вектор Akejk. Построение переходной функции табличным методом. Изображение переходной функции можно представить в виде: 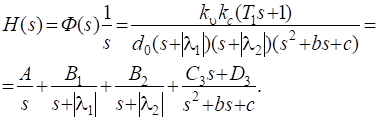 Здесь b=2, c=2+2. Приведем полученное выражение к общему знаменателю и приравняем числитель этого выражения к числителю исходного изображения переходной функции. Приравняв члены при одинаковых степенях оператора s в правой и левой частях, получим систему линейных уравнений относительно неопределенных коэффициентов. Из этой системы сразу определяется А=1, после чего решается система 4-го порядка. 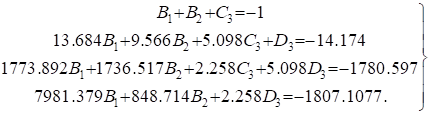 Решение этой системы дает: 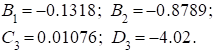 Три первых слагаемых изображения переходной функции являются табличными. Необходимо преобразовать к табличному виду четвертое слагаемое. 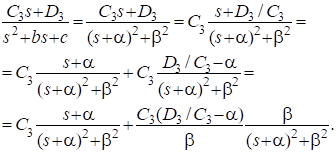 Полученные слагаемые являются табличными. Подставив численные значения параметров и использовав таблицы преобразования Лапласа, получим выражение для переходной функции 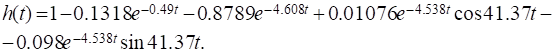 автоматизированный управление качество интегральный Построение переходной функции с использованием формулы разложения. Вначале определим составляющие процесса, соответствующие вещественным корням. 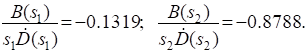 Для колебательной составляющей получим 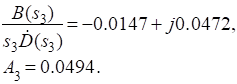 Так как вектор этой составляющей находится во втором квадранте, то Следовательно 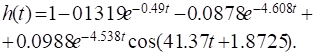 Переходные процессы, полученные различными способами совпадают с точностью до арифметических вычислений. Кривая переходной функции показана на рис. 2. Переходный процесс практически монотонный. Колебательная составляющая фактически ни как себя не проявляет ввиду крайне малой амплитуды. Перерегулирование отсутствует: =0. Время регулирования, определенное при =0.05, приближенно равно 2.2 с., что для системы автоматического регулирования угла тангажа в большинстве случаев является вполне приемлемым. Рис. 2. Переходная функция системы регулирования угла тангажа Импульсная переходная (весовая) функция системы (звена). Построение импульсной переходной характеристики. Связь между весовой и переходной функциями. Весовая функция (импульсная переходная функция) называется функция, которая описывает реакцию системы, когда на ее вход подается  Если в качестве математической модели системы управления принята передаточная функция, то можно получить: 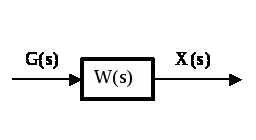 Следовательно, весовая функция Переходной функцией h(t) называется реакция звена на единичное ступенчатое воздействие, т.е. переходный процесс на выходе Х2 при единичном скачке 1(t) на входе звена x1. Следовательно, 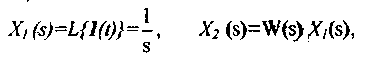 откуда Поскольку известно, что (имея в виду обобщенные функции) 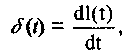 то имеем следующее соотношение между весовой и переходной функциями 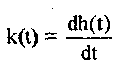 Из определений переходной и весовой функций автоматического управления имеем: Сравнивая эти два равенства нетрудно заметить, что Весовая и переходная функции являются исчерпывающими характеристиками систем автоматического управления при нулевых начальных условиях. По этим характеристикам можно однозначно определить выходную переменную 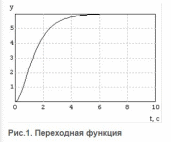 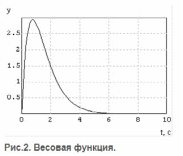 Понятие элементарного (типового) звена. Основные виды типовых звеньев. Пропорциональное (усилительное звено) и его временные и частотные характеристики. Звеном САУ называют математическую модель элемента или соединения элементов любой части системы. Звенья, как и системы, могут описываться дифференциальными уравнениями высокого порядка и в общем случае ихпередаточные функции могут быть представлены как 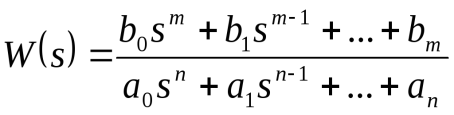 . (4.63) . (4.63)Но их можно представить как соединения типовых или элементарных звеньев, порядок дифференциальных уравнений которых не выше второго. Из курса алгебры на основании теоремы Безу известно, что полином произвольного порядка можно разложить на простые множители вида Поэтому передаточную функцию (4.63) можно представить, как произведение простых множителей вида (4.64) и простых дробей вида Звенья, передаточные функции которых имеют вид простых множителей (4.63) или простых дробей (4.64), называют типовыми или элементарными звеньями. Прежде чем переходить к изучению элементарных звеньев, вспомним формулы для модуля и аргумента комплексного числа. Пусть комплексное число представлено в виде отношения двух произведений комплексных чисел Так как Таким образом, справедливо следующее правило модулей и аргументов комплексных чисел: модуль комплексного числа, представленного в виде отношения двух произведений комплексных чисел, равен отношению произведения модулей сомножителей числителя к произведению модулей сомножителей знаменателя, а его аргумент - разности суммы аргументов сомножителей числителя и суммы аргументов сомножителей знаменателя. Виды типовых звеньев : - Пропорциональное звено - Интегрирующее звено. - Дифференцирующее звено. - Апериодическое звено. - Форсирующее звено - Колебательное звено Пропорциональное (усилительное звено) и его временные и частотные характеристики. Передаточная функция Временные характеристики можно определить по известным характеристикам безынерционного и интегрирующего звеньев – . 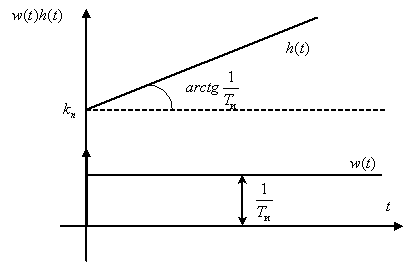 Частотная характеристика 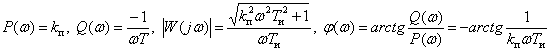 . .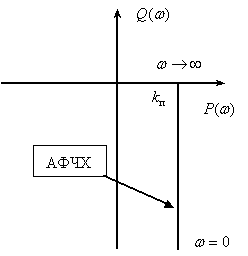 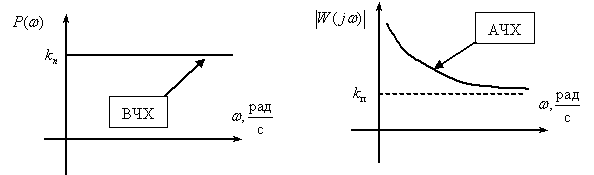 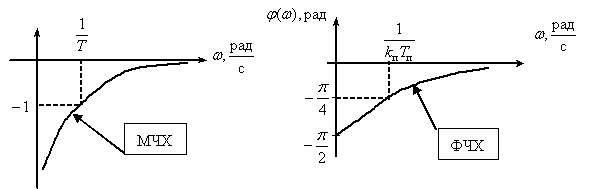 Интегрирующее звено и его временные и частотные характеристики. Передаточная функция Преобразуем передаточную функцию реального дифференцирующего звена для удобства получения временных характеристик – где Временные характеристики можно определить по известным характеристикам интегрирующего и апериодического звеньев – 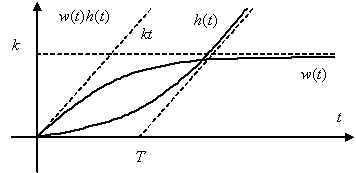 Частотная характеристика  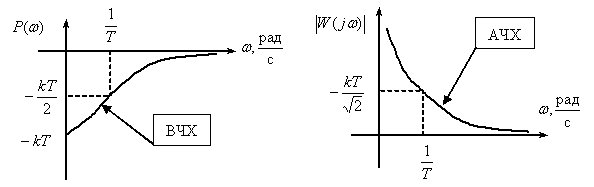 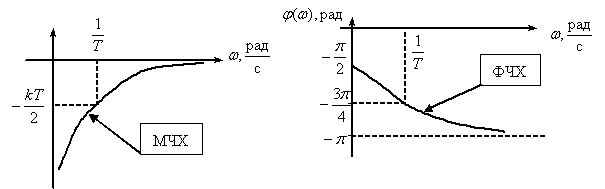 Идеальное дифференцирующее звено и его временные и частотные характеристики. Уравнение идеального дифференцирующего звена y(t) = kx¢(t), (7.15) то есть изменение выходной координаты пропорционально скорости изменения входной координаты. Передаточная функция Частотные характеристики изображены на рис. 7.4: АФХ: W(iw) = k×iw = kweip/2; (7.17) АЧХ: M(w) = kw; (7.18) ФЧХ: j(w) = p/2. (7.19) 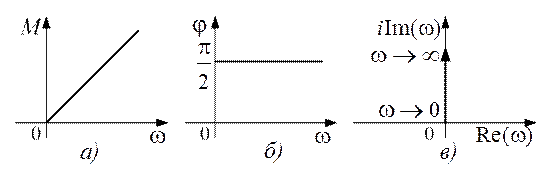 Рис. 7.4. Частотные характеристики идеального дифференцирующего звена: а) АЧХ; б) ФЧХ; в) АФХ АЧХ прямо пропорциональна частоте, а ФЧХ не зависит от частоты и равна π/2. Годограф АФХ совпадает с положительной ветвью мнимой оси. Переходная функция идеального дифференцирующего звена имеет вид: h(t) = k×1¢(t) = kd(t), (7.20) то есть представляет собой δ-функцию с площадью, равной k. Весовая функция представляет собой производную от δ-функция w(t) = kd¢(t). (7.21) Временные характеристики изображены на рис. 7.5. 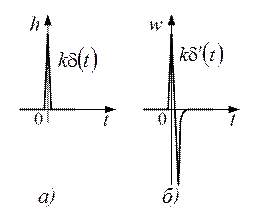 Рис. 7.5. Переходные характеристики идеального дифференцирующего звена: а) переходная функция; б) весовая функция Реальное дифференцирующее звено и его временные и частотные характеристики. Передаточная функция . Преобразуем передаточную функцию реального дифференцирующего звена для удобства получения временных характеристик – Временные характеристики можно определить по известным характеристикам безынерционного и апериодического звеньев – 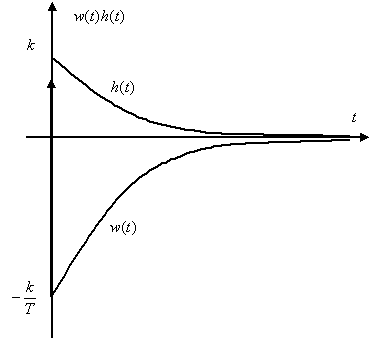 Частотная характеристика 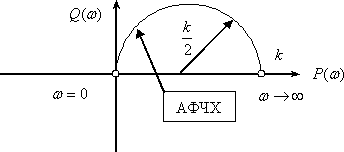 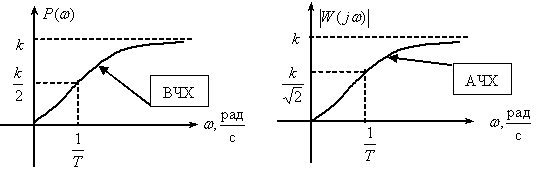 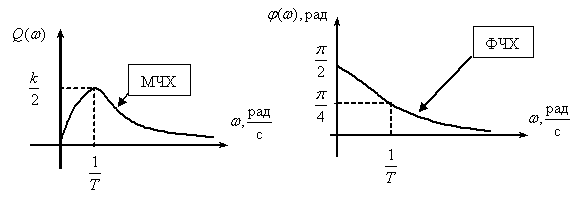 .Апериодическое звено первого порядка, его временные и частотные характеристики.ф Передаточная функция . Временные характеристики 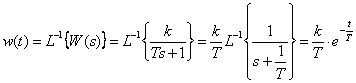 , ,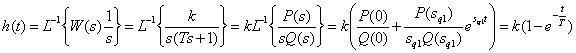 . .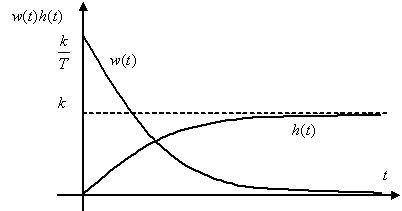 Частотная характеристика 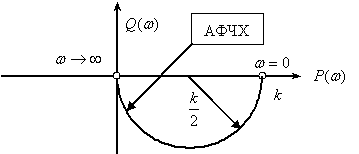 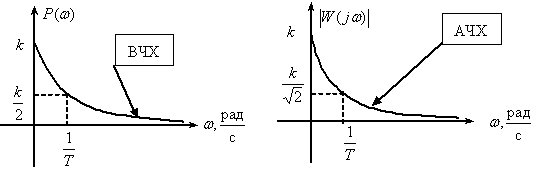 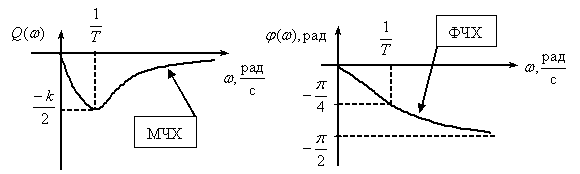 Колебательное звено и его временные и частотные характеристики. Колебательное звено является звеном второго порядка и описывается дифференциальным уравнением второго порядка Характеристическое уравнение звена Передаточная функция 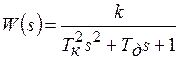 . (8.23) . (8.23)Частотные характеристики изображены на рис. 8.8: АФХ: 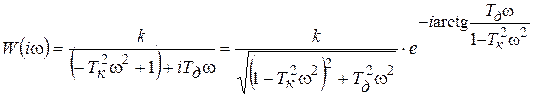 .(8.24) .(8.24)АЧХ: 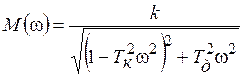 ; (8.25) ; (8.25)ФЧХ: 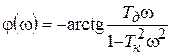 . (8.26) . (8.26)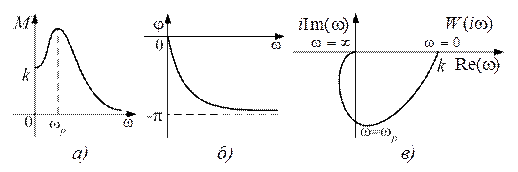 Рис. 8.8 Частотные характеристики колебательного звена: а) АЧХ; б) ФЧХ; в) АФХ При больших значениях Тк/Тд на графике АЧХ появляется максимум и при Tд ® 0 АЧХ терпит разрыв второго рода при значении wр=1/Тк Графики переходных функций изображены на рис. 8.9. Переходная функция h(t)=k[1+Ae−atsin(wt−b)], (8.27) где 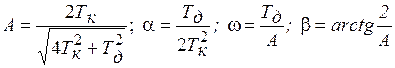 . .Весовая функция w(t)=−Aαe−αtsin(ωt−β)+Aωe−αtcos(ωt−β)=Ae−αt(cos(ωt−β)−α×sin(ωt−β)). (8.28) Частным случаем колебательного звена является консервативное звено, у которого характеристическое уравнение имеет только мнимые корни. В этом случае передаточная функция звена преобразуется к виду 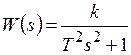 . (8.29) . (8.29)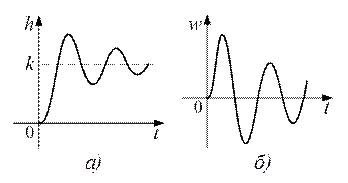 Рис. 8.9. Переходные характеристики колебательного звена: а - переходная функция; б - весовая функция Частотные характеристики (рис. 8.10): АФХ: 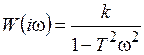 ; (8.30) ; (8.30)АЧХ: 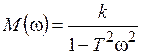 ; (8.31) ; (8.31)ФЧХ: 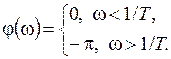 (8.32) (8.32)Годограф АФХ расположен на действительной полуоси комплексной плоскости. 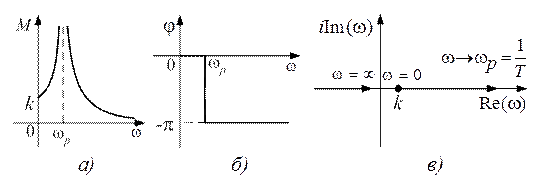 Рис. 8.11. Частотные характеристики консервативного звена: а) АЧХ; б) ФЧХ; в) АФХ Временные характеристики представляют собой гармонические колебания. Частота wp=1/T называется резонансной частотой (рис. 8.12). Переходная функция: 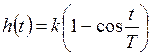 . (8.33) . (8.33)Весовая функция: 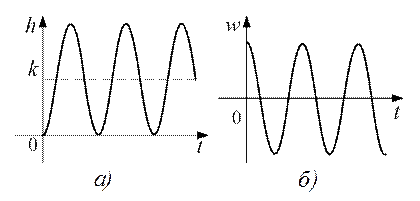 Рис. 8.12 Функции консервативного звена: а) переходная; б) весовая Консервативное звено и его временные и частотные характеристики. Это звено получается при мнимых полюсах передаточной функции (3.1) и его можно рассматривать как частный случай колебательного звена при Ь, = 0. Выражения для передаточной и некоторых частотных функций звена будут иметь вид 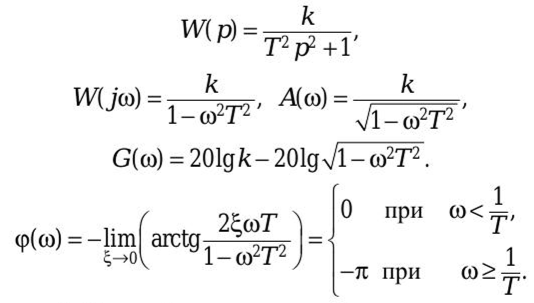 На рис. 3.13а изображены логарифмические частотные характеристики консервативного звена. Точная ЛАЧХ (сплошная линия) терпит разрыв непрерывности второго рода на частоте сопряжения Переходная функция консервативного звена может быть получена по формуле (2.10) при мнимых полюсах имеет вид На рис 3.13, б показана переходная характеристика консервативного звена, она представляет собой незатухающие автоколебания частотой 1/Т и амплитудой к. Консервативное звено на пассивных четырехполюсниках не реализуется. Если обратиться к приведенному выше примеру (см. рис. 2.6), то должны отсутствовать потери в контуре, т. е. выполняться условие Д = 0, что физически невозможно. В устройстве, схема которого приведена на рис. 3.12а, в соответствии с формулами (3.5) получение консервативного звена возможно при В^-оо. Для этого резистор Д просто нужно удалить из устройства. 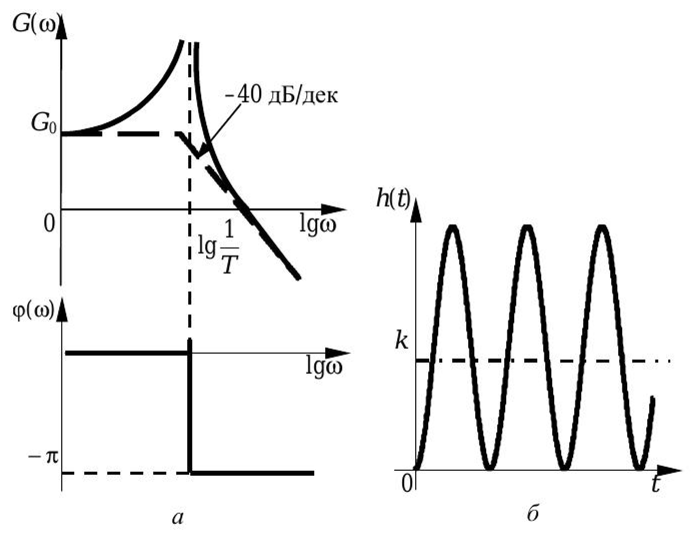 Рис. 3.13. ЛАЧХ, ЛФЧХ (а), переходная характеристика (б) консервативного звена Апериодическое звено второго порядка и его временные и частотные характеристики. Уравнение апериодического звена второго порядка T1T2y''(t) + (T1 + T2)y′(t) + y(t) = kx(t). (8.15) Передаточная функция звена равна 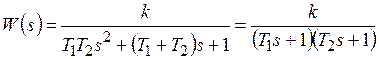 . (8.16) . (8.16)Апериодическое звено второго порядка можно представить в виде последовательного соединения двух звеньев первого порядка с постоянными времени Т1и T2, поэтому оно не относится к числу элементарных. Корни характеристического уравнения действительные. Частотные характеристики изображены на рис. 8.6: АФХ: 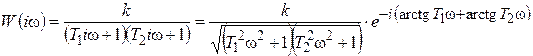 ;(8.17) ;(8.17)АЧХ: 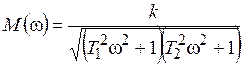 ; (8.18) ; (8.18)ФЧХ: j(w)= –(arctgT1w + arctgT2w). (8.19) Пунктиром показаны частотные характеристики апериодического звена первого порядка. При сравнении частотных характеристик видно, что добавление второго апериодического звена первого порядка увеличивает инерционность объекта. 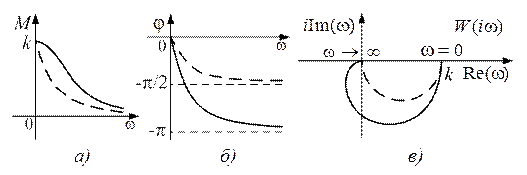 Рис. 8.6. Частотные характеристики апериодического звена второго порядка: а) АЧХ; б) ФЧХ; в) АФХ Переходные характеристики изображены на рис. 8.7. Переходная функция где 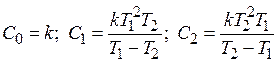 , ,представляет собой неколебательную кривую, имеющую одну точку перегиба и асимптотически стремящуюся к y(∞) = k. Весовая функция 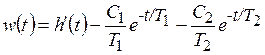 . (8.21) . (8.21)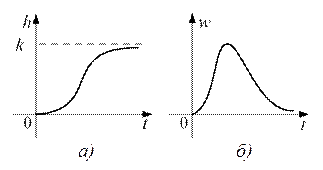 Рис. 8.7 Переходные характеристики апериодического звена второго порядка: а) переходная функция; б) весовая функция Звено чистого запаздывания и его временные и частотные характеристики. Уравнение звена чистого запаздывания y(t) = x(t – τ). (7.36) Передаточная функция: W(s) = e–sτ. (7.37) Графики частотных характеристик изображены на рис. 7.10: АФХ: W(iw) = e–iwτ; (7.38) АЧХ: M(ω) = 1; (7.39) ФЧХ: j(ω) = –wt. (7.40) 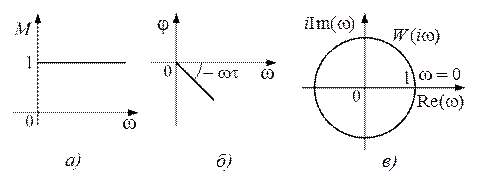 Риc. 7.10. Частотные характеристики звена чистого запаздывания: а) АЧХ; б) ФЧХ; в) АФХ Так как М(ω) = 1, а отставание по фазе выходных колебаний прямо пропорционально частоте с коэффициентом пропорциональности равным времени чистого запаздывания, то годограф АФХ представляет собой окружность единичного радиуса с центром в начале координат. Переходные характеристики: переходная функция: h(t) = 1(t – τ); (7.41) весовая функция: w(t) = (t – τ). (7.42) Графики переходных характеристик изображены на рис. 7.11. 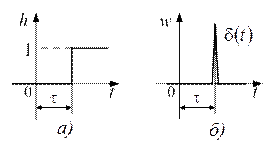 Рис. 7.11. Переходные характеристики звена чистого запаздывания: а) переходная функция; б) весовая функция Форсирующие звенья и их характеристики Форсирующим звеном называется звено, описываемое уравнением 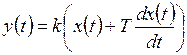 . (7.29) . (7.29)Передаточная функция W(s) = k(1 + Ts). (7.30) Частотные характеристики форсирующего звена показаны на рис. 5.9: АФХ: АЧХ: ФЧХ: j(w) = arctgwT. ...(7.33) 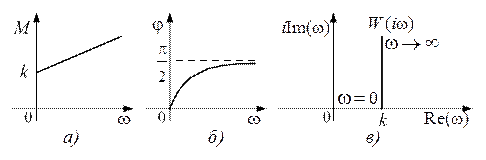 Рис. 7.8. Частотные характеристики форсирующего звена: а) АЧХ; б) ФЧХ; в) АФХ Переходная функция: h(t) = k(1(t) +Td(t)); (7.34) весовая функция: w(t) = k(d(t) + Td¢(t)). (7.35) Графически переходные характеристики представлены на рис. 7.9. 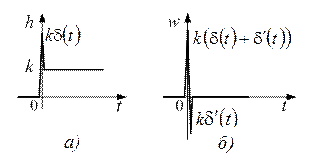 Рис. 7.9. Переходные характеристики форсирующего звена: а) переходная функция; б) весовая функция Структурные схемы линейных систем. Условные обозначения звеньев, сигналов, сравнивающих элементов, сумматоров и узлов. Виды соединений звеньев в структурных схемах. Структурные схемы линейных САУ Под структурной схемой САУ будем понимать её графическое изображение, отображающее её элементы и связи с точки зрения их передаточных функций и взаимодействия. Структурная схема выступает в качестве динамического эквивалента реальной системы САУ. Она может быть получена по дифференциальному уравнению связи и по передаточным функциям. Элементы на структурной схеме обозначаются прямоугольниками внутри которых записывается передаточная функция К(р), слева входной, а справа выходной сигналы. Определение передаточной функции по структурной схеме При анализе структурных схем оперируют четырьмя передаточными функциями: 1. Передаточная функция разомкнутой системы W(p) 2. Передаточная функция замкнутой системы Ф(р) 3. Передаточная функция по ошибке ФD(р) 4. Передаточная функция по внешнему воздействию ФF (р) 1) W(p) – передаточная функция рассчитывается как отношение хвых (р) к Dх(р) при отбросе всех возмущающих воздействий и обратной связи и при отброшенном задающем воздействии 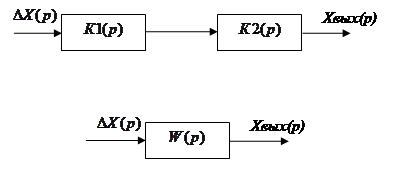 2) Ф(р) – передаточная функция рассчитанная при отброшенном возмущающем воздействии  3)  4) ФF (р) – определяется при отброшенном воздействии хвх (р).  Все передаточные функции однозначно связанны между собой передаточной функцией разомкнутой системы W(p), следовательно, о качестве САУ можно судить по передаточной функции W(p). В свою очередь передаточная функция разомкнутой системы определяется передаточными функциями и параметрами отдельных элементов входящих в ее состав. Поэтому важно знать характеристики отдельных элементов и звеньев.
|
