ответы на вопросы. ответы на билеты тау. Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем

• Название: Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем
• Анкор: ответы на вопросы
• Дата: 22.05.2022
• Размер: 1.89 Mb.
• Имя файла: ответы на билеты тау.docx
• Тип: Документы; #542500
• страница: 3 из 7

Типовые воздействия в системах управления. Их математическое описание. Виды динамических характеристик.

Типовые воздействия это типовые функции времени, подаваемые на вход устройства, по реакции на которые определяются динамические характеристики устройства в переходном режиме. Переходным режимом считается режим перехода технического устройства из одного состояния в другое. Считается, что состояние технического устройства в фиксированный момент времени определяется значением его обобщенных координат. Рассмотрим типовые воздействия.

                 Типовое воздействие 1 ( t )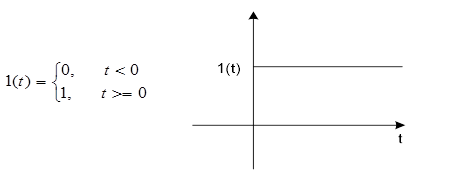      

                                                                  

Реакция системы управления на функцию 1(t) называется переходной функцией или переходной характеристикой и обозначается h(t).

                 Импульсная  дельта - функция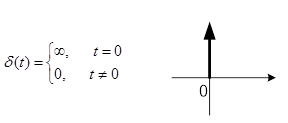



     Реакция системы управления на  импульсную дельта - функцию называется импульсной переходной функцией, функцией веса, весовой функцией. Обозначим ее через   (t). Особенность дельта - функции заключается в том, что она имеет единичную площадь: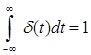

                                                  .

Отметим, что импульсная переходная функция зависит только от интервала времени между моментом начала действия импульса  и данным моментом времени t. Важно знать, что импульсная переходная  функция  (t) системы и переходная характеристика h(t) связаны соотношением:

                          .

Передаточная функция непрерывной линейной стационарной системы определяется через преобразование Лапласа ее весовой функции, а именно: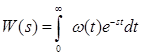

                        

Типовые воздействия 1(t) и  (t) являются наиболее неблагоприятными для работы технических устройств и их элементов. Если качество управления удовлетворительно при типовых воздействиях, то тем более оно будет удовлетворительно при обычных режимах работы.

                Гармоническая функция

Гармонические функции на входе и выходе устройства могут быть

представлены  следующим образом:

g_вх (t) =A_вх sin w t,       g_вых (t) =A_вых sin (w t + Y).

Частотные характеристики A(w) и Y(w) описывают установившиеся вынужденные колебания, полученные при подаче на вход устройства гармонического воздействия. A(w) - амплитудно - частотная характеристика. Y(w) – фазо-частотная характеристика.

Динамические характеристики определяют свойства системы, когда на ее вход подают сигналы, меняющиеся во времени. В зависимости от вида входного воздействия различают временные и частотные характеристики. На рисунке 28 показана классификация динамических характеристик систем автоматического управления.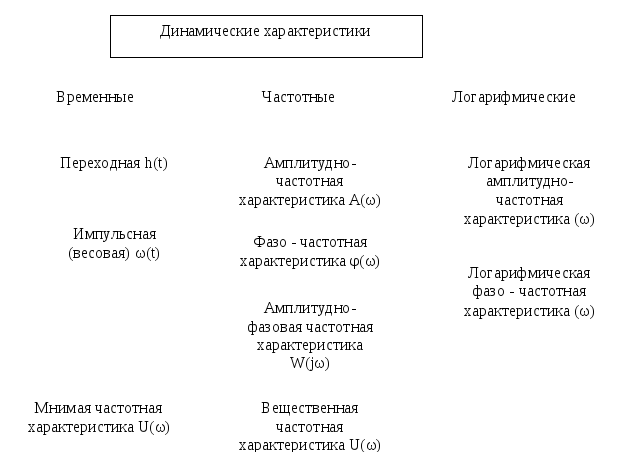



Рис. 28. Классификация динамических характеристик.

10. 
    Частотные характеристики. Физический смысл частотных характеристик. Виды частотных характеристик и методика их получения и построения.
    

Рассмотрим уравнение в операторной форме для линейной системы (11). Для системы с одним входом по управлению выражение (11) преобразуется к виду

(28)

Его передаточная функция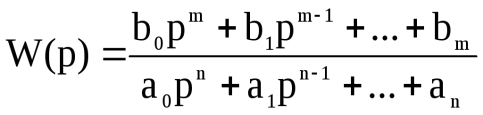

(29)

Найдем математическое описание вынужденного движения системы, описываемого уравнением (28) при подаче на ее вход гармонического воздействия  . Общее решение системы имеет вид: , где - общее решение неоднородного уравнения, а - частное решение неоднородного уравнения. Составляющая определяет свободное движение или переходной процесс. В устойчивых системах она со временем затухает. Вынужденное решение описывает частное решение . Пусть на вход подается гармонический сигнал . Используя формулу Эйлера для преобразования гармонической функции, входной сигнал преобразуется к виду . Данное преобразование представляет в виде суммы двух сигналов

(30)

где  , а .

Частное решение уравнения (28) будем искать в виде

(31)

Используя формулу Эйлера и принцип суперпозиции выражение (31) преобразуется к виду

(32)

где  , а .

Для линейных систем справедлив принцип суперпозиции: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности.

Подставив по очереди первые и вторые слагаемые выражений (30) и (32) в уравнение (28), имеем соотношения:

для первого слагаемого и

для второго слагаемого

Выражение для первой составляющей выходного сигнала преобразуется к виду: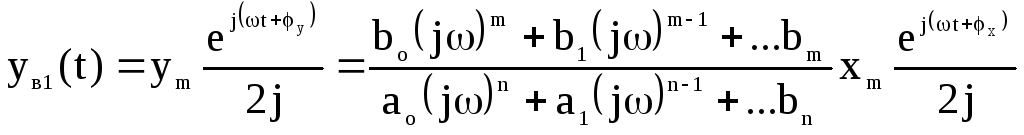

(33)

Это есть не что иное, как произведение передаточной функции на входной сигнал  . Оператор дифференцирования р в передаточной функции (29) приобретает значение соответствующей степени как результат операции дифференцирования. Соответственно уравнение (33) можно записать в следующем виде



Рассуждая аналогичным образом, получают решение для второго слагаемого выражения (32)



Сложив между собой результаты выражений для  и , получают представление уравнения (32) для описания вынужденного движения системы при гармоническом воздействии

(34)

Таким образом, полученное решение в виде уравнения (34) позволяет сделать вывод, что при гармоническом воздействии в устойчивых системах выходная величина также изменяется по гармоническому закону, но с другими значениями амплитуды и фазы.

При этом отношение амплитуд входной и выходной величин равны модулю, а сдвиг фаз – аргументу передаточной функции. С точки зрения практического применения это означает, что в уравнение для передаточной функции (29) вместо оператора дифференцирования р следует подставить 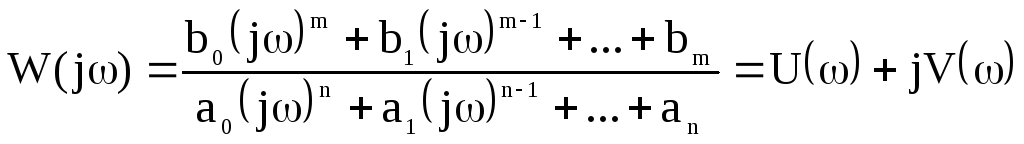. Полученное выражение определяет амплитудно-фазовую характеристику (АФХ)

(35)

АФХ - зависимость отношения комплексов выходного и входного сигналов от частоты  . АФХ имеет две формы записи: в показательной - и в алгебраической - . Уравнение (35) определяет алгебраическую форму записи.

Амплитудно-частотная характеристика (АЧХ) - это зависимость амплитуды выходного сигнала к амплитуде входного сигнала в зависимости от частоты:

(36)

Фазо - частотная характеристика (ФЧХ) - зависимость разности (сдвига) фаз колебаний выходного и входного сигналов от частоты:

(37)

Вещественная частотная характеристика (ВЧХ) – это зависимость действительной части АФХ от частоты, мнимая частотная характеристика (МЧХ) – зависимость мнимой части АФХ от частоты.

Характеристики АЧХ, ФЧХ, ВЧХ, МЧХ являются скалярными величинами и строятся в прямоугольной системе координат, где по оси абсцисс откладывается частота, а по оси ординат соответствующая функция.

АФХ не является скаляром. Каждое значение АФХ – комплексная величина, которая рассматривается как вектор на комплексной плоскости с координатами 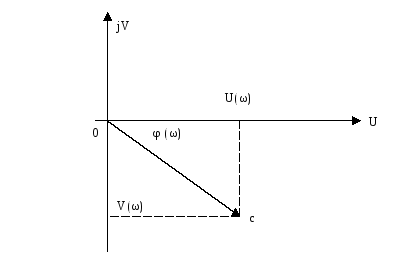 и . АФХ есть годограф вектора при изменении частоты от 0 до . На рисунке 29 дана представление АФХ на комплексной плоскости.



Рис.29. Представление АФХ на комплексной плоскости

Длина вектора, проведенного из начала координат в любую точку годографа характеризует значение АЧХ, а угол между положительным направлением вещественной полуоси и вектором дает значение ФЧХ для заданного значения частоты.

Формула (35) для вычисления АФХ позволяют выразить АЧХ и ФЧХ через ВЧХ и МЧХ. Уравнение (36) для расчета АЧХ приобретет вид



Выражение (37) для ФЧХ запишется как

при 

При  к правой части последнего равенства следует добавить рад для получения углов во втором и третьем квадрантах комплексной плоскости.

Частотные характеристики определяются из частотной передаточной функции



Используются следующие виды частотных характеристик.

1. 
   Амплитудно-фазовая частотная характеристика – АФЧХ или АФХ
   

Это годограф, описываемый концом вектора W(jω)при изменении частоты 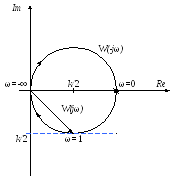. (для отрицательных частот годограф строится как зеркальное отражение относительно вещественной оси)

Пример: 

2. 
   Амплитудно-частотная характеристика(АЧХ) и фазовая частотная характеристика (ФЧХ).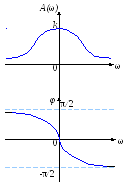
   

- АЧХ - четная функция частоты

- ФЧХ - нечетная функция частоты

3. 
   Вещественная частотная и мнимая частотная характеристики.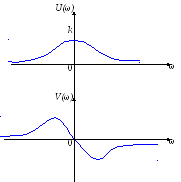
   

4. 
   Логарифмические частотные характеристики (ЛЧХ).
   

• 
  логарифмическая амплитудная частотная характеристика (ЛАЧХ).
  
• 
  логарифмическая фазовая частотная характеристика (ЛФЧХ).
  

Логарифмические частотные характеристики строятся в прямоугольных координатах. По оси абсцисс откладываются частота в логарифмическом масштабе, т.е по этой оси линейным оказывается масштаб по lgω. В ЛАЧХ по оси ординат откладывается модуль частотного передаточного коэффициента, представленный в децибелах. . (Прим.: Бел – логарифмическая единица отношения двух величин, обозначается Б. Названа в честь изобретателя телефона Белла). В ЛФЧХ по оси ординат откладывается фаза обычным образом в градусах либо радианах.

Логарифмический масштаб по оси частот.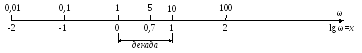



Логарифмические характеристики всегда рассматриваются совместно друг под другом.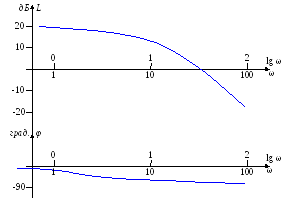

10. 
    Логарифмические частотные характеристики (ЛЧХ) Понятие логарифмической амплитудной частотной функции. Логарифмическая амплитудная частотная характеристика. Логарифмическая фазовая частотная характеристика.
    

При исследовании систем управления частотные характеристики удобно строить в логарифмических координатах по таким причинам: 1) в большинстве случаев АЧХ звеньев в логарифмических координатах можно представить отрезками прямых линий; 2) АЧХ цепочки звеньев графически суммируются.

АЧХ в логарифмических координатах строится в виде зависимости lg A от lg ω, называемой логарифмической амплитудно–частотной характеристикой (ЛАЧХ), а фазовая – в виде зависимости φ от lg ω, наз. логарифмической фазочастотной характеристикой (ЛФЧХ).

При этом за единицу масштаба частоты принимается декада – частотный интервал, соответствующий изменению частоты в 10 раз.

При построении ЛАЧХ по оси ординат откладывают выходную величину L(ω), измеряемую в децибелах (дБ). Бел – единица десятичного логарифма коэффициента усиления мощности сигнала. Один бел соответствует усилению мощности в 10 раз, 2 бела – в 100 раз, 3 бела – в 1000 раз и т.д.

Поскольку мощность сигнала пропорциональна А², то ее усиление в белах в логарифмических координатах равно lg A² = 2 lg A (в децибелах – 20 lg A.).

Таким образом – L(ω) = 20 lg A(ω).

Соотношение A и L приведено в следующей таблице

А (раз)	0,01	0,1	0,5	1,0	1,12	1,41	2,0	3,6
L (дБ)	–40	–20	–6

При построении ЛФЧХ фаза откладывается по оси ординат в радианах или угловых градусах в обычном масштабе, т.к. фазовый сдвиг цепочки звеньев равен сумме фазовых сдвигов на отдельных ее звеньях. При совместном анализе ЛАЧХ и ЛФЧХ на оси абсцисс применяют логарифмический масштаб частоты в декадах или в октавах (одна октава соответствует изменению частоты в два раза).

Отметим, что при использовании логарифмического масштаба точка, соответствующая ω = 0, находится в минус ∞, а нулю на оси абсцисс соответствует точка ω = 1 рад/с.

В расчетах и анализе САУ широкое применение находят частотные характеристики в логарифмических масштабах. Применение логарифмического масштаба позволяет наглядно изображать характеристики в большом диапазоне частот, представлять характеристики отрезками ломанных линий и определять характеристики сложных систем простым суммированием характеристик, входящих в эти системы элементов.

Логарифмические характеристики имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.

Логарифмические амплитудная (ЛАЧХ) и фазовая (ЛФЧХ) частотные характеристики, получаются путем логарифмирования передаточной функции:

lg[W(jw)] = lg[A(w) exp(jj(w)] = lg[A(w)]+lg[exp(jj(w)] = L(w) + j(w).

ЛАЧХ получают из первого слагаемого, которое умножается на 20:

L(w)=20 lg A(w). (2.18)

Логарифмическая амплитудная частотная характеристика (ЛАЧХ) звена или САУ строится в прямоугольной системе координат, где по оси ординат в линейном масштабе указывается величина ЛАЧХ в децибелах, а по оси абсцисс в логарифмическом масштабе указывается частота w в 1/с (при этом равномерные изменения частоты в 10 раз представляются декадами). Декада [дек] – любой отрезок, на котором значение частоты   увеличивается в десять раз. Децибел равен 1/10 бела. Бел равен десятичному логарифму отношения мощностей на выходе и входе звена или пропорциональному мощностям отношению квадратов напряжений, токов, скоростей или других физических величин (1 бел = lgP₂/P₁ = lgU₂₂/U₁₂). Поэтому в (2.18) множитель 20 = 2∙10, где 2 отражает логарифмирование квадрата отношения выходной и входной величин, а 10 — перевод белов в децибелы.

Ось абсцисс должна проходить через точку 0 дБ, что соответствует модулю A(w)=1, т.к. логарифм единицы равен нулю.

Ось ординат может пересекать ось абсцисс в произвольном месте, но обычно её проводят так, чтобы справа можно было разместить всю ЛАЧХ.

Логарифмическая фазовая частотная характеристика (ЛФЧХ) j(w)= arctg[V(w)/U(w)] звена или САУ строится по оси ординат в линейном масштабе, где указывается угол фазового сдвига j(w)в радианах или градусах, а по оси абсцисс указывается частота w в логарифмическом масштабе в 1/с, как в ЛАЧХ. Для элементарных звеньев она не выходит за пределы: -p ≤ j ≤ p. При построении фазовой частотной характеристики логарифмический масштаб применяют только для оси абсцисс. ЛФЧХ, отличается от ФЧХ только масштабом по оси w.

Примеры ЛАЧХ и ЛФЧХ показаны на рис. 2.13.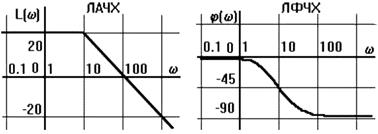



 

Рис. 2.13

На рис.2.14 показана ЛАЧХ L(w) (толстая линия) и соответствующая ей приближенная (асимптотическая) характеристика L_а(w) в виде прямолинейных отрезков (тонкая линия). Частоты, соответствующие точкам стыковки отрезков, называют сопрягающими и обозначают w_с. Максимальное отличие реальных ЛАЧХ от асимптотических обычно не превышает 3дБ при w =w_с.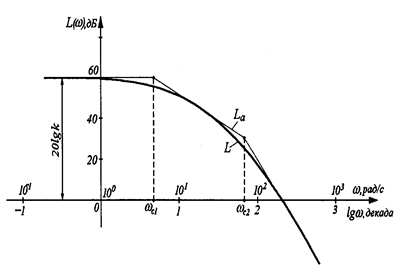



Рис.2.14

 

Частота, на которой L(w) = 0, т.е. A(w) = 1, называется частотой среза w_ср. Она соответствует точке пересечения ЛАЧХ с осью абсцисс. Верхняя полуплоскость ЛАХ соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость - значениям А<1 (ослабление амплитуды).

Во многих случаях логарифмические амплитудные частотные характеристики можно построить практически без вычислительной работы. Если частотную передаточную функцию САУ представить в виде произведения сомножителей ПФ её элементов, то результирующую ЛАЧХ можно отобразить в виде асимптотической характеристики, представляющей ломаную линию, состоящую из отрезков прямых линий с наклонами, кратными величине 20дБ/дек. Физический смысл наклона – 20 дБ/дек: при увеличении частоты в 10 раз амплитуда выходного сигнала уменьшается в 10 раз, соответственно наклон – 40 дБ/дек – означает уменьшение амплитуды в 100 раз.