ответы на вопросы. ответы на билеты тау. Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем

• Название: Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем
• Анкор: ответы на вопросы
• Дата: 22.05.2022
• Размер: 1.89 Mb.
• Имя файла: ответы на билеты тау.docx
• Тип: Документы; #542500
• страница: 6 из 7

Правило, передаточная функция параллельного соединения звеньев равна сумме передаточных функций отдельных звеньев, т.е.

25. 
    Встречно-параллельное соединение звеньев. Положительная и отрицательная обратная связь. Передаточная функция этого соединения.
    

Подача сигнала с выхода звена на его вход называется обратной связью. На рис. 6.15 звено 1 охвачено обратной связью с помощью звена 2. Звено 2 называют звеном обратной связи.

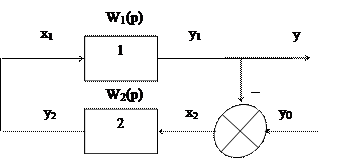
Рис. 6.15. Встречно–параллельное соединение звеньев

Различают положительную и отрицательную обратные связи. Если сигнал обратной связи увеличивает входной сигнал, то связь положительная, в противном случае – отрицательная.

Если в качестве звена обратной связи используется усилительное звено, то связь называется жесткой. Если дифференциальное звено – имеем гибкую обратную связь.

Рассмотрим два важных практических случая. Звено 1 – объект регулирования, звено 2 – регулятор. Звенья 1 и 2 вместе образуют замкнутую систему регулирования. Различают передаточные функции такой системы по нагрузке и по заданию.

6.5.4 Передаточная функция по нагрузке W_н(p) говорит о том, что возмущение в системе приложено к объекту регулирования (см. рис. 6.14). Для этой системы можно записать следующие соотношения сигналов:

х = х₁ = х_{2 ;} х₁ = х – у₂

у₁ = W₁(p) × х₁ ; у₂ = W₂(p) × у _.

у = у₁ = W₁(р) × х₁ = W₁(р) × (х – у₂) = W₁(p) × [х – W₂(р) × х₂] =

= W₁(p) × [х – W₂(р) × у] = W₁(p) × х – W₁(p) × W₂(р) × у .

Отсюда – у × [1 + W₁(p) × W₂(p)] = W₁(p) × x .

Таким образом, передаточная функция по нагрузке имеет вид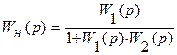

 .

Передаточная функция разомкнутой системы – Wp(p) = W₁(p)×W₂(p).

Тогда передаточная функция по нагрузке замкнутой системы на рис. 6.15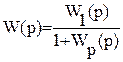

 .

6.5.5 Передаточная функция по заданию Wз(p) означает, что возмущение в системе приложено к регулятору (рис. 6.16).

Рис. 6.16. Встречно–параллельное соединение звеньев

с передаточной функцией по нагрузке

Для такой системы управления можно записать следующие соотношения сигналов:

у = у₁; х = у₂; х₁ = у₀ – у₁.

у₁ = W₁(p) × х₁ ; у₂ = W₂(p) × х₂ ; Wз(p) = у / у₀ .

у = у₁ = W₁(р) × х₁ = W₁(р) × у₂ = W₁(p) × W₂(р) × х₂ =

= W₁(p) × W₂(р) × (у₀ – у) = W₁(p) × W₂(р) × у₀ – W₁(p) × W₂(р) × у .

Отсюда – у × [1 + W₁(p) × W₂(p)] = W₁(p) × W₂(р) × у₀ .

Таким образом, передаточная функция по заданию имеет вид

 .

Или 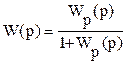  , где W(p) – ПФ разомкнутой системы.

25. 
    Правила переноса сумматоров и узлов в структурных схемах автоматических систем регулирования. Перестановка узлов и сумматоров.
    

В тех случаях, когда структурная схема оказывается слишком сложной, например, содержит перекрестные связи, ее упрощают, пользуясь правилами преобразования структурных схем. Смысл этих правил состоит в переносе элементов структурной схемы из одного положения в другое, так чтобы при этом сохранялась эквивалентность структурных схем.

1. Перенос узла через звено.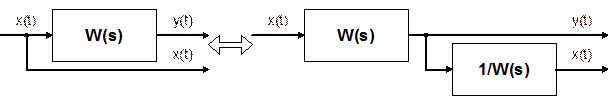



Чтобы перенести узел через звено с передаточной функцией W(s), необходимо включить в линию, не проходящую через звено (выход 2), дополнительный элемент – звено с передаточной функцией 1/W(s). Убедимся, что эти схемы эквивалентны. Действительно, сигнал у(t) после такого переноса не изменится, а сигнал на выходе 2 будет равен: Х(s)·W(s)·1/W(s) = Х(s), т.е. он совпадает с исходным сигналом х(s).

2. Перенос звена через узел.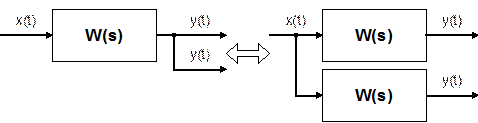



Чтобы перенести звено с передаточной функцией W(s) через узел, необходимо включить в обе линии звенья с передаточной функцией W(s). Легко убедиться, что эквивалентность структурных схем при этом сохраняется.

3. Перенос сумматора через звено.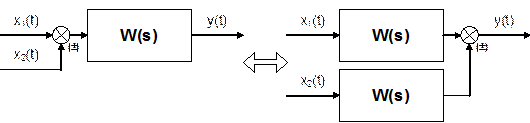



Сразу отметим, что данное правило преобразования структурных схем применимо как к сумматорам, так и к элементам сравнения, т.к. элемент сравнения можно рассматривать как сумматор с инвертированным входом.

Чтобы перенести сумматор через звено с передаточной функцией W(s), необходимо к обоим входам на сумматор добавить дополнительный элемент – звено с передаточной функцией W(s). Убедимся, что эти схемы эквивалентны. Выходной сигнал на исходной схеме равен: Y(s) = W(s)·[X₁(s) ± X₂(s)]; выходной сигнал на преобразованной схеме равен: Y(s) = W(s)X₁(s) ± W(s)X₂(s), т.е. выходные сигналы совпадают.

4. Перенос звена через сумматор.



Это правило преобразования структурных схем также применимо как к сумматорам, так и к элементам сравнения. Чтобы перенести звено с передаточной функцией W(s) через сумматор, необходимо в линию без звена (вход 2) включить дополнительный элемент – звено с передаточной функцией 1/W(s). Убедимся, что эти схемы эквивалентны. Выходной сигнал на исходной схеме равен: Y(s) = W(s)·X₁(s) ± X₂(s); выходной сигнал на преобразованной схеме равен: Y(s) = W(s)·[X₁(s) ± 1/W(s)·X₂(s)] = W(s)·X₁(s) ± X₂(s), т.е. выходные сигналы совпадают.

5. Перенос узла через сумматор.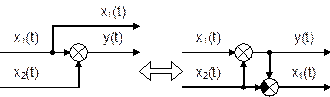



Чтобы перенести узел через сумматор, необходимо в схему включить дополнительный элемент – элемент сравнения. Эти схемы эквивалентны, т.к. выходные сигналы совпадают: у(t) = х₁(t) + х₂(t) и х₁(t) = у(t) – х₂(t) = х₁(t) + х₂(t) – х₂(t).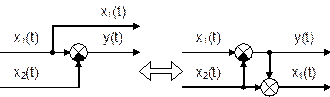



При применении этого правила преобразования структурных схем для переноса узла через элемент сравнения в схему необходимо включить дополнительно не элемент сравнения, а сумматор. Эквивалентность этих схем также легко проверить: у(t) = х₁(t) – х₂(t) и х₁(t) = у(t) + х₂(t) = х₁(t) – х₂(t) + х₂(t).


6. Перенос сумматора через узел.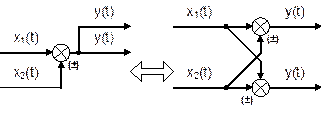



Это правило преобразования структурных схем применимо как к сумматорам, так и к элементам сравнения. Чтобы перенести сумматор через узел, необходимо в схему включить дополнительный сумматор. Эти схемы эквивалентны, т.к. выходные сигналы совпадают: у(t) = х₁(t) + х₂(t).

7. Перенос сумматора через сумматор.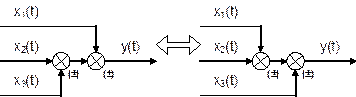



Это правило преобразования структурных схем фактически реализует правило коммутативности сложения в математике – от перестановки мест слагаемых сумма не изменяется. Оно, разумеется, применимо как к сумматорам, так и к элементам сравнения.

8. Перенос звена через звено.



Это правило преобразования структурных схем фактически реализует правило коммутативности умножения в математике – от перестановки мест множителей произведение не изменяется.

9. Перенос узла через узел.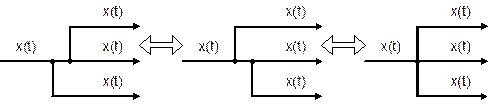

25. 
    Передаточная функция одноконтурной системы. Передаточная функция замкнутой системы по задающему, возмущающему воздействиям относительно выходной величины.
    

Замкнутая система называется одноконтурной, если при ее размыкании (сразу после сумматора) получается цепочка из последовательно соединенных звеньев или цепь, не содержащая параллельных соединений и обратных связей.



Рисунок 12– Пример одноконтурной системы

Прямая цепь – участок по ходу сигнала от точки приложения входного воздействия до точки съема выходного сигнала.

Разомкнутая цепь – цепь из последовательно соединенных звеньев, входящих в замкнутый контур.

Для одноконтурной системы справедливо правило:

Передаточная функция одноконтурной системы с отрицательной (положительной) обратной связью равна передаточной функции прямой цепи деленной на единицу плюс (минус) передаточная функция разомкнутой системы.

В замкнутой системе регулируемая величина   через

обратную связь подается на её вход (на элемент сравнения). В общем случае к системе приложены задающее   и возмущающее воздействие F(p). Оба эти воздействия оказывают влияние на регули­руемую величину   . Поэтому при анализе замкнутой системы необхо­димо рассматривать передаточные функции, связывающие   с   и   с F(p) .

В качестве примера рассмотрим одноконтурную CAP, схема которой представлена на рис.4.23.

К этой схеме можно свести все одноконтурные CAP, струк­турные схемы которых могут со­держать вместо указанных звеньев любое число последова­тельно или параллельно соединённых звеньев, а также звеньев, охваченных местными обратны­ми связями. Здесь   - выходная регулируемая величина,   - воз­мущение, а   - задающее воздействие. Выведем выражения для передаточных функций, связывающих   с   и   .

Рассмотрим вначале передаточную функцию CAP по задающему воздействию. В этом случае   и   .Следует отметить, что в одноконтурных CAP в качестве главной обратной связи применяется отрицательная обратная вязь. Это объясняется тем, что в замкнутых CAP используется принцип регулирова­ния «по отклонению» выходной величины от заданного значения. В этом случае все изменения выходной регулируемой величины, вызванные воз­мущениями, будут ликвидироваться в результате противоположного дей­ствия управляющего устройства CAP.

С учетом сказанного передаточная функция CAP по задающему воз­действию определится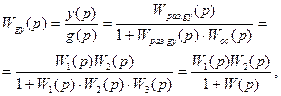

 (4.24)

где   передаточная функция разомкнутой САР в случае одиночной обратной связи;

 передаточная функция разомкнутой системы при задающем воздействии   .

Передаточная функция САР по возмущающему воздействию, связывающая выходную регулируемую величину 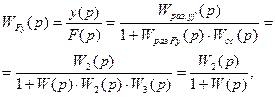  с возмущающим воздействием   , приложенным в произвольной точке системы, будет иметь вид

 (4.25)

где   передаточная функция разомкнутой системы при возмущающем воздействии   .

Следовательно,

 (4.26)

 (4.27)

25. 
    Передаточная функция одноконтурной системы относительно ошибки по задающему и возмущающему воздействиям.
    

Определение передаточной функции по ошибке по задающему воздействию: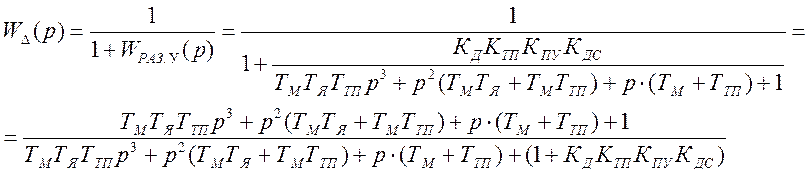



Передаточная функция по ошибке по возмущающему воздействию: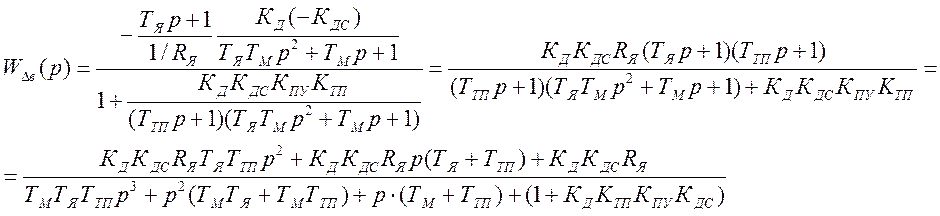

25. 
    Передаточная функция многоконтурной системы.
    

Замкнутая система называется многоконтурной если при ее размыкании получается цепь, содержащая параллельные и обратные связи, или иначе если она кроме главной обратной вязи содержит параллельные или местные обратные связи.

Многоконтурная система имеет перекрещивающиеся связи, если контур обратной или параллельной связи охватывает участок цепи, содержащий только начало или конец другой цепи обратной или параллельной связи.

Для вычисления передаточной функции многоконтурной системы необходимо прежде всего перестановкой и переносом узлов и сумматоров освободиться от перекрещивающихся связей. Затем, используя правила преобразования структурных схем, преобразовать ее в одноконтурную систему. Следует иметь в виду, что при преобразовании структурной схемы нельзя переносить сумматор через точку съема выходного сигнала, так как при этом точка съема оказывается на неэквивалентном участке линии связи.

К многоконтурным относятся системы радиоавтоматики, в которых помимо замкнутого контура с главной обратной связью имеются контуры, образованные стабилизирующими обратными связями, введёнными для придания системе нужных динамических характеристик. Передаточные функции таких систем находятся путём последовательного сведения структурной схемы многоконтурной системы к эквивалентной одноконтурной.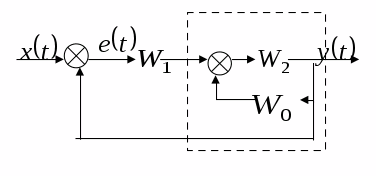



Рис. 3.8. Cтруктурная схема двухконтурной системы

Исходя из вышеизложенного, передаточная функция системы, структурная схема которой изображена на рис.3.8, находится следующим образом:

1). Сначала находится передаточная функция внутреннего контура, изображённого на рисунке штриховкой, который является системой с обратной связью:

 .

2). Если представить внутренний контур как отдельное звено, то вся система представляется как последовательная система, состоящая из двух звеньев. Тогда её передаточная функция находится следующим образом:

.




Например, при переносе сумматора через звено по направлению сигнала 
(рис. 2.33), в структуру добавляется звено с передаточной функцией  (р), при этом изображение выходного сигнала до и после преобразования одинаково:

                             (2.67)

что свидетельствует об эквивалентности исходной и преобразованной структур.

При переносе сумматора через звено против направления сигнала  (рис. 2 34)  в исходную структуру добавляется звено с передаточной функцией   . И в этом  случае сигнал на выходе структуры сохраняется неизменным и равным  (2.67).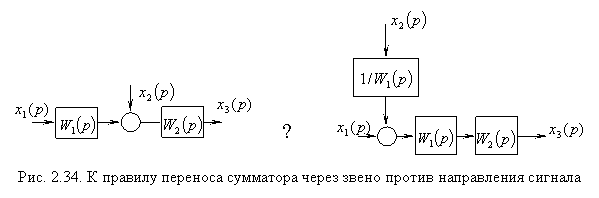




На примере структуры, приведенной на рис. 2.35, а, проиллюстрировано правило переноса точки съема сигнала чрез звено по направлению сигнала (рис. 2.35, б) и в противоположном направлении (рис. 2.35, в)

Используя рассмотренные выше правила, структурную схему, приведенную на рис. 2.32,  можно преобразовать к виду, в котором перекрестные связи отсутствуют (рис. 2.36, а). 

Передаточные функции  звеньев, входящих в преобразованную структуру системы, приведенную на рис. 2.36, б: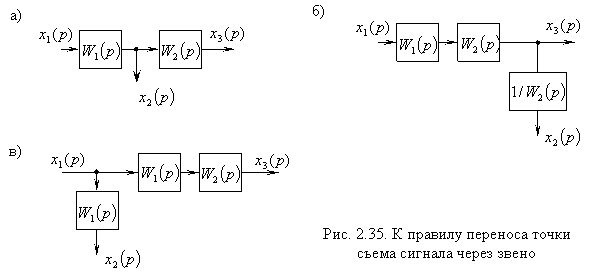

;     ;     




Передаточная функция замкнутой системы:

Ф(р) = 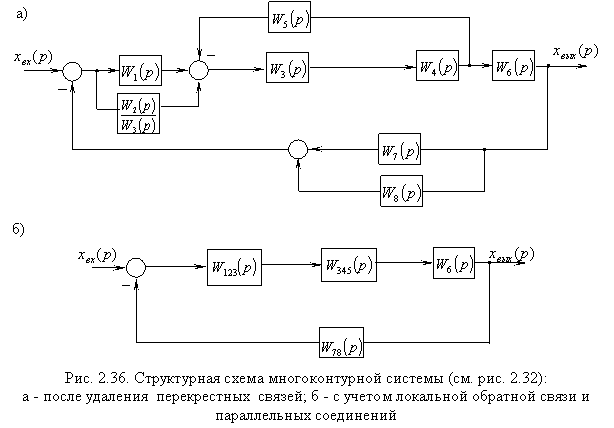  .