|
|
ответы на вопросы. ответы на билеты тау. Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем
Часть системы, математическая модель элемента
|
х y W(s) – передаточная функция звена
|
 Элемент сравнения Элемент сравнения
|
Устройство, выполняющее операцию вычитания сигналов
|
х1 у = х1-х2 х2
|
 Сумматор Сумматор
|
Устройство, выполняющее операцию суммирования сигналов
|
х1 у = х1+х2 х2
|
Узел
|
Точка разветвления сигнала
|
х х х х
|
Систему автоматического управления можно рассматривать как комбинацию типовых динамических звеньев. Изображение системы управления в виде совокупности типовых и нетиповых динамических звеньев с указанием связей между ними носит название структурной схемы системы. Звено в этом случае выступает как элементарная структурная единица, преобразователь информации.
Структурные схемы состоят из отдельных структурных элементов. Основными элементами структурных схем являются следующие.
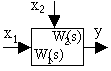
1. Звено с одним входом и одним выходом: Y(s)=W(s)X(s).
Звено с двумя входами и одним выходом (около каждого входа записывается своя передаточная функция):Y(s)=W1(s)X1(s)+W2(s)X2(s)
3. Линия связи и узел (разветвление), стрелка показывает направление передачи информации.
 и и
4. Сумматор.
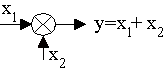
5. Элемент сравнения.
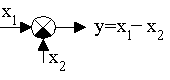 или или 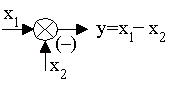
В системах управления встречаются три вида соединений звеньев: последовательное, параллельное и соединение по схеме с обратной связью.
Последовательное соединение звеньев изображено на рис.3.10, такое соединение характеризуется тем, что выход предыдущего звена подается на вход последующего.
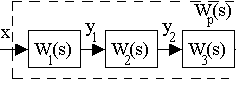 
Рис. 3.10. Последовательное соединение звеньев
Выходная величина последовательно соединенных звеньев определяется 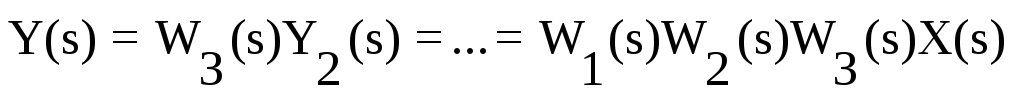 . .
Откуда результирующая передаточная функция равняется
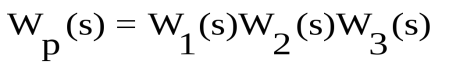 . .
Следовательно, в общем случае можно записать
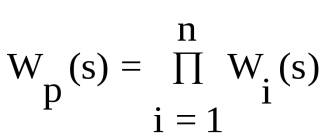 , (3.51) , (3.51)
где n - число включенных последовательно звеньев.
Таким образом, результирующая передаточная функция последовательно соединенных звеньев равна произведению передаточных функций составляющих звеньев.
Параллельное соединение звеньев изображено на рис.3.11, такое соединение характеризуется тем, что на входы всех звеньев подается одно и то же входное воздействие, а выходная величина определяется суммой выходных величин отдельных звеньев.
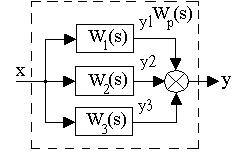
Рис. 3.11. Параллельное соединение звеньев
Выходная величина параллельно соединенных звеньев определяется y=y1+y2+y3, т.е.
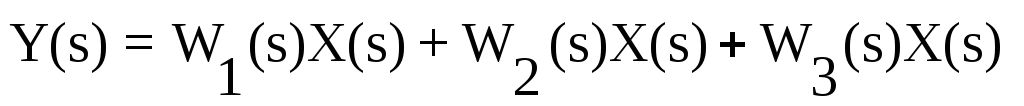 . .
Тогда 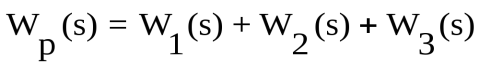 . .
В общем случае
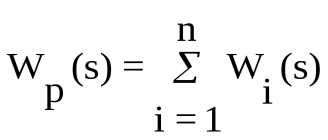 , (3.52) , (3.52)
где n - число включенных параллельно звеньев.
Таким образом, результирующая передаточная функция параллельно соединенных звеньев равна сумме передаточных функций составляющих звеньев.
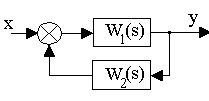
Обратная связь. Такое соединение звеньев изображено на рис.3.12, оно характеризуется тем, что выходной сигнал звена подается на его вход.
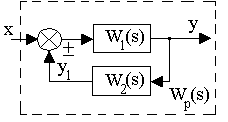
Рис. 3.12. Соединение звеньев по схеме с обратной связью
Обратная связь может быть положительной (ПОС), если сигнал y1, снимаемый с выхода второго звена, суммируется с сигналом x на входе, и отрицательной (ООС), если y1 вычитается. Кроме того, обратные связи могут быть жесткими и гибкими. Связь называется гибкой, если передаточная функция W2(s) в установившемся режиме равна нулю.
Для определения результирующей передаточной функции такой комбинации звеньев запишем очевидные соотношения:
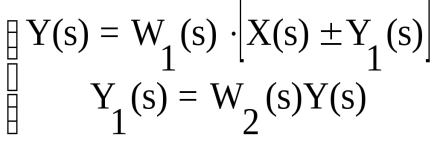 , ,
где знак “+” относится к положительной, а знак “-” - к отрицательной обратной связи.
Откуда результирующая передаточная функция обратной связи имеет вид
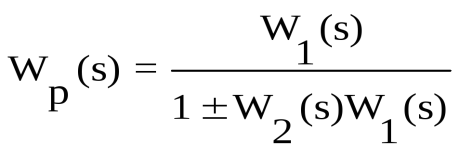 , (3.53) , (3.53)
где знак “+” соответствует ООС, знак “” - ПОС.
В общем случае, сложная цепь динамических звеньев, образующих систему управления, включает в себя комбинации всех трех рассмотренных случаев, т.е. представляет собой смешанное соединение звеньев. Пользуясь выражениями (3.51), (3.52) и (3.53), можно найти общую результирующую передаточную функцию смешанного соединения звеньев.
В тех случаях, когда структурная схема системы оказывается сложной и содержит перекрестные связи, ее упрощают и сводят к простейшему эквивалентному виду, пользуясь правилами преобразования структурных схем [1,2,7].
Основные правила эквивалентного преобразования структурных схем.
1. Перенос сумматора:
а)
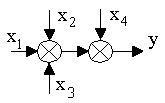 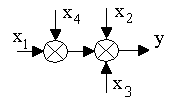
y = x1+x2+x3+x4 y = x1+x4+x2+x3
б)
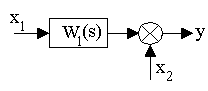 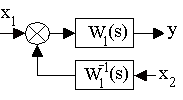
y = x1W1(s)+x2 y = [x1+x2W1-1(s)] W1(s) = x1W1(s)+x2
2. Перенос узла:
а)
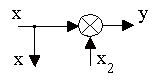 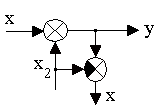
б)
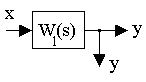 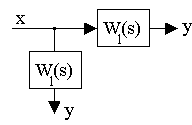
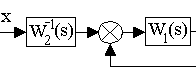
3. Преобразование к единичной обратной связи.
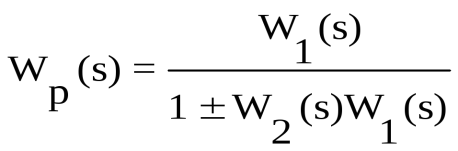 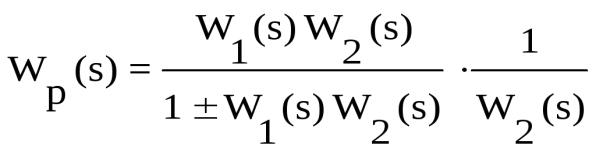
Построение логарифмических частотных характеристик
разомкнутой цепи звеньев
Логарифмические частотные характеристики имеют большое практическое значение. Поэтому рассмотрим их построение. В общем случае частотные характеристики строят по методике, изложенной в разделе 3.1. Однако часто результирующую передаточную функцию смешанного соединения звеньев можно свести к виду
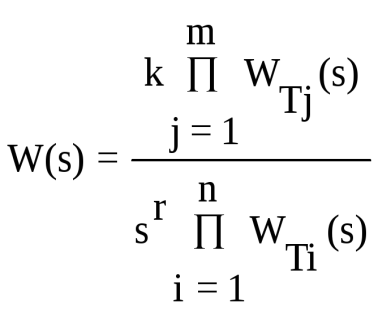 , (3.54) , (3.54)
где WT(s) - передаточная функция типового звена.
В этом случае построение ЛАХ производится по выражению
L() = 20lgA() = 20lgW(j)=
= 20lgk - r20lg +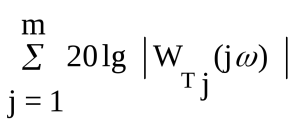 - -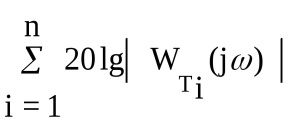 . .
Построение ЛФХ производится по выражению
() = argW(j) = -r900 + 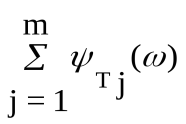 - -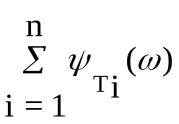 . .
Таким образом, результирующая ЛАХ определяется суммированием ЛАХ составляющих типовых звеньев, а результирующая ЛФХ - соответственно суммированием ЛФХ составляющих типовых звеньев. Таблицы характеристик типовых звеньев имеются в литературе [1,7].
Асимптотические ЛАХ можно построить непосредственно по виду передаточной функции (3.54) по следующему правилу, состоящему из четырех пунктов.
1. Частотная область разбивается на диапазоны, границы которых определяются сопрягающими частотами, соответствующими постоянным времени передаточной функции:
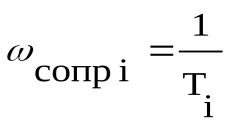 . .
Число сопрягающих частот равняется числу постоянных времени в передаточной функции, а число частотных диапазонов на единицу больше.
2. Первая низкочастотная асимптота ЛАХ, которая проводится в крайнем левом низкочастотном диапазоне, имеет наклон (20r)дб/дек и проходит через точку с координатами: =1 с-1, L(1)=20lg k дб, где r - показатель степени оператора Лапласа s, записанного в знаменателе передаточной функции (3.54).
3. На сопрягающих частотах ЛАХ претерпевает изломы.
3.1. Если сопрягающая частота соответствует постоянной времени Тi, находящейся в знаменателе передаточной функции, то ЛАХ делает излом вниз на (20v)дб/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Тi.
3.2. Если сопрягающая частота соответствует постоянной времени Тi, находящейся в числителе передаточной функции, то ЛАХ делает излом вверх на +(20v) дб/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Тi.
4. Вторая асимптота проводится до следующей сопрягающей частоты и так далее.
Пример. Построить ЛАХ звена, имеющего следующую передаточную функцию: 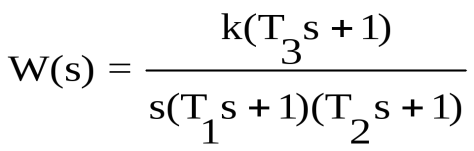 , ,
где k = 100 с-1 ; Т1= 5 с; Т2= 0.01 с; Т3= 0.5 с.
Решение.
1. Представим передаточную функцию, как комбинацию типовых звеньев:
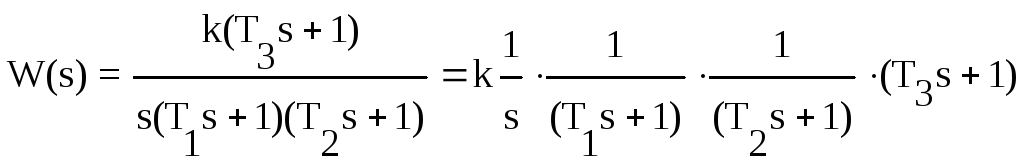 . .
2. Находим сопрягающие частоты:
сопр1= 1/Т1= 0.2 с-1; сопр2= 1/Т2= 100 с-1; сопр3= 1/Т2= 2 с-1.
Строим ЛАХ.
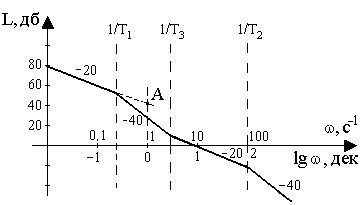
Рис. 3.13. Логарифмическая частотная характеристика звена
3.1. Частотную область разбиваем на четыре диапазона.
Низкочастотный участок ЛАХ имеет наклон
(20r)= (201)= 20дб/дек и проходит через точку с координатами: = 1с-1, L(1) = 20lg k = 40дб (точка А[1,40]).
На частоте 1/Т1 ЛАХ делает излом вниз на
(20v)= (201)= 20 дб/дек.
На частоте 1/Т3 ЛАХ делает излом вверх на
(20v) = (201) = 20дб/дек.
3.5. На частоте 1/Т2 ЛАХ делает излом вниз на
(20v) = (201) = 20 дб/дек.
Вид полученной ЛАХ приведен на рис. 3.13.
Используя то же правило, по ЛАХ звена можно однозначно определить передаточную функцию.
Последовательное соединение звеньев. Передаточная функция последовательного соединения.
Последовательным называется такое соединение звеньев, при котором выходная величина одного звена подается на вход последующего звена.
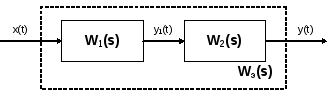
Для этого соединения справедливы следующие соотношения:
Y1(s) = W1(s)·X(s) Y(s) = W2(s)·Y1(s) = W1(s)·W2(s)·X(s) = Wэ(s)·X(s)
Wэ(s) = W1(s)·W2(s)
Для случая последовательного соединения n звеньев имеем:
Wэ(s) = W1(s)·W2(s)·…·Wn(s)
Другими словами, эквивалентная передаточная функция цепи последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев. Таким образом цепочку параллельных звеньев в структурной схеме можно заменить одним звеном с передаточной функцией Wэ(s) = W1(s)·W2(s)·…·Wn(s).
Рассмотрим последовательное соединение типовых звеньев и найдем выражение для общей передаточной функции.

Рис. 3.26. Структурная схема
последовательного соединения звеньев.
Утверждение: передаточная функция последовательного соединения звеньев равна произведению передаточных функций всех звеньев.
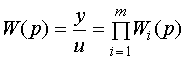 , ,
|
(3.52)
|
Для доказательства найдем выходную переменную системы
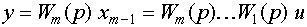
Отношение y к u дает передаточную функцию (3.52).
Параллельное соединение звеньев. Его особенности и передаточная функция.
Параллельным соединением звеньев называется такое соединение, при котором на выход всех элементов поступает одно и то же воздействие, а их выходные величины алгебраически суммируются (рис. 13):
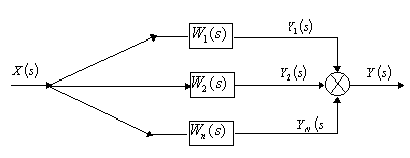
Рис. 13. Параллельное соединение звеньев
Введем обозначения:
 – узел разветвления сигнала, – узел разветвления сигнала,
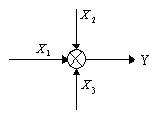 – узел суммирования сигналов. – узел суммирования сигналов.
Запишем уравнение движения в преобразованном по Лапласу виде:
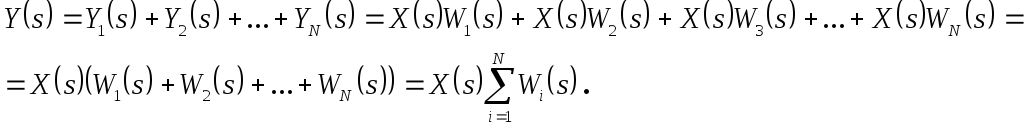
Или
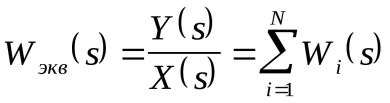 .(48) .(48)
|
|
 Скачать 1.89 Mb.
Скачать 1.89 Mb.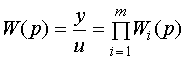 ,
,
 – узел разветвления сигнала,
– узел разветвления сигнала, – узел суммирования сигналов.
– узел суммирования сигналов.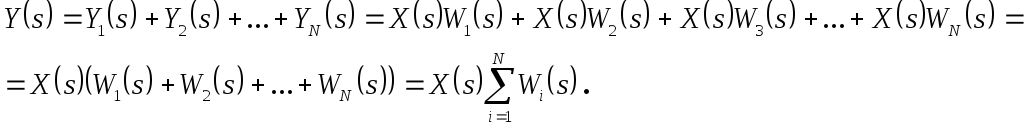


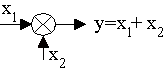
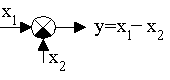 или
или 
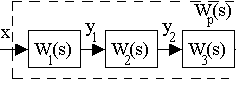
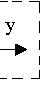
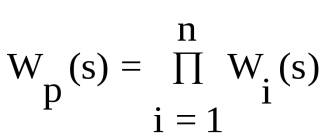 , (3.51)
, (3.51)
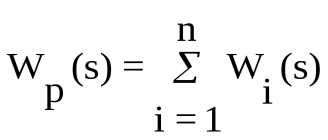 , (3.52)
, (3.52)
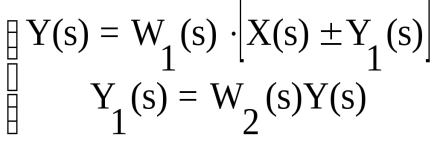 ,
,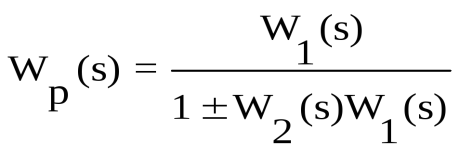 , (3.53)
, (3.53)








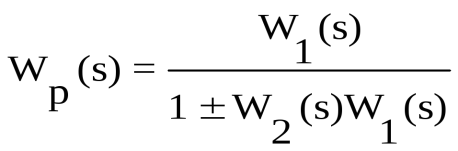
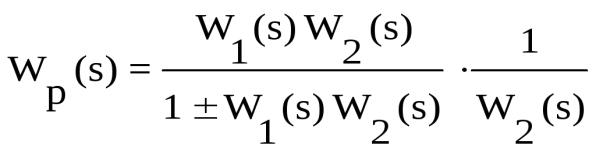
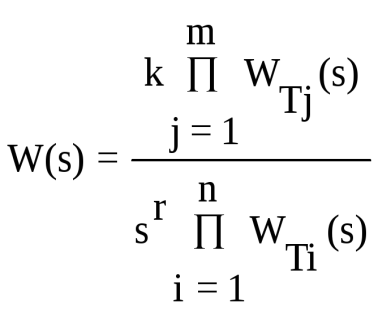 , (3.54)
, (3.54)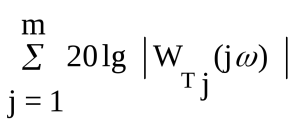 -
-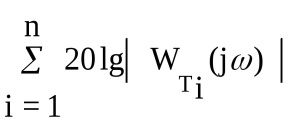 .
.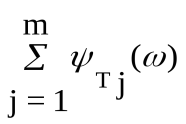 -
-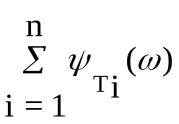 .
.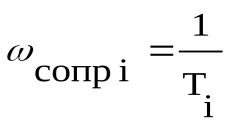 .
.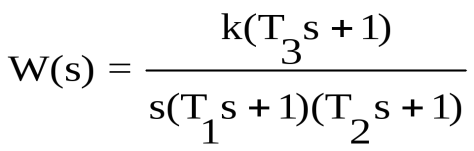 ,
,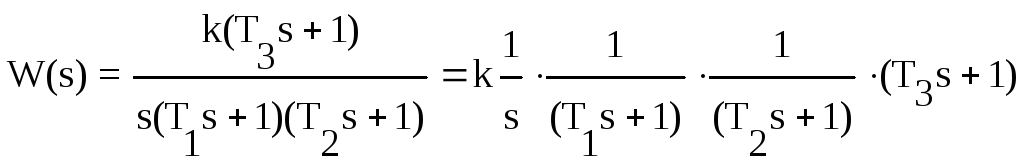 .
.
