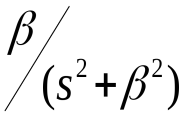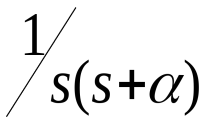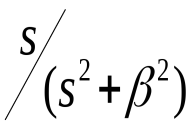ответы на вопросы. ответы на билеты тау. Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем

• Название: Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем
• Анкор: ответы на вопросы
• Дата: 22.05.2022
• Размер: 1.89 Mb.
• Имя файла: ответы на билеты тау.docx
• Тип: Документы; #542500
• страница: 2 из 7

Линеаризация нелинейных уравнений статики и динамики. Применение разложения в ряд Тейлора для линеаризации нелинейных функций. Геометрическая линеаризация нелинейных характеристик.

Поведение реальных систем обычно описывается нелинейными уравнениями. Решение таких уравнений довольно сложно, нахождение даже приближенного численного решения требует большого объема вычислений. Поэтому при инженерных методах анализа и расчета реальных систем применяют линеаризацию уравнений: нелинейные уравнения заменяют приближенными линейными, решать которые значительно проще.

Часто нелинейной бывает лишь статическая характеристика системы или ее элементов. Так, нелинейную характеристику имеет резервуар для газа, входной величиной которого является степень открытия вентиля на линии поступления газа, а выходной -- давление газа в аппарате.

Непрерывно дифференцируемую нелинейную статическую характеристику можно линеаризовать, например, по методу малых отклонений. Для этого функцию разлагают в ряд Тейлора в окрестности точки, соответствующей нормальному (заданному) режиму работы системы, в данном случае это точка А с координатами х_вх 0и х_вых 0 (рис. I-3).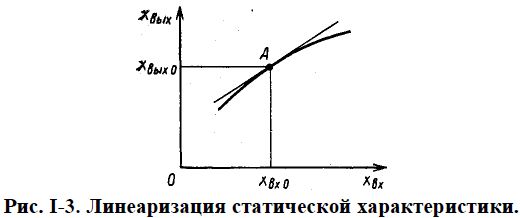



Отбрасывая члены ряда, содержащие бесконечно малые величины второго и более высоких порядков, получим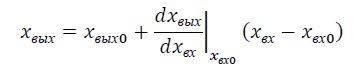



Эта зависимость представляет собой уравнение прямой линии, касательной к линеаризуемой функции при значении аргумента х_вх 0. Введя обозначения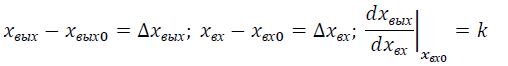



Получим



Некоторые простые функции (произведение, частное от деления переменных х, у и др.) можно линеаризовать, подставив в них вместо переменных х, у выражения типа (x₀+Дx), (y₀+Дy). Выполнив математические операции, предписываемые линеаризуемыми функциями, и исключив из полученных зависимостей слагаемые, содержащие приращения второго и более высоких порядков, получают искомую линеаризованную функцию. Например, линеаризация произведения двух переменных проводится следующим образом:



Принимая во внимание, что x₀y₀=z₀ найдем



Аналогичным образом линеаризуют и уравнения динамики.

Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1: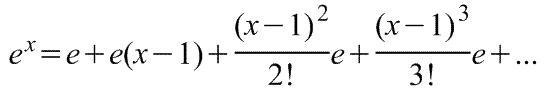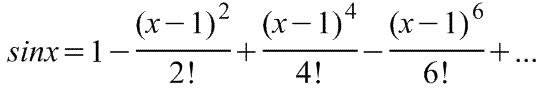





При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.

Ряд Тейлора в окрестности точки a имеет виды:

1) 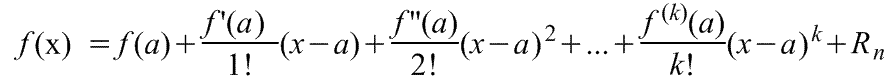, где f(x) - функция, имеющая при х=а производные всех порядков. R_n - остаточный член в ряде Тейлора определяется выражением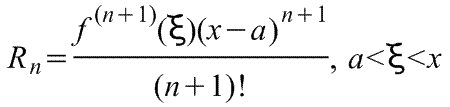 

2)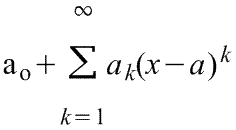

k-тый коэффициент (при х_k) ряда определяется формулой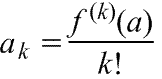



3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)

при a=0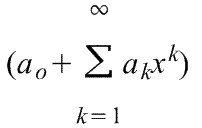 

члены ряда определяются по формуле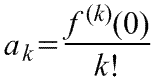



Условия применения рядов Тейлора.

1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).

2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.

Свойства рядов Тейлора.

1. 
   Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
   
2. 
   Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например: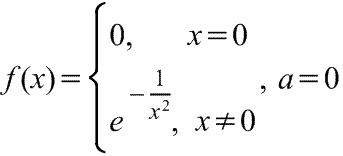
   

Ряды Тейлора применяются при аппроксимации ( приближение - научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от  linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.

Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.

Линеаризация-замена реальных нелинейных уравнений статических характеристик элементов близкими к ним линейными уравнениями. Линеаризация возможна, если нелинейная характеристика непрерывна и имеет непрерывные частные производные. На рис.2.1. приведена геометрическая интерпретация линеаризации по методу малых отклонений.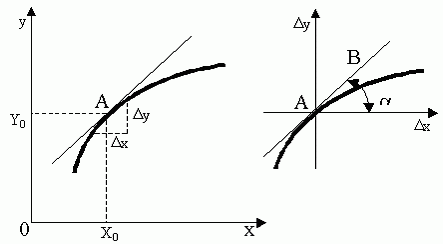

 

Рис.2.1. Геометрическая интерпретация линеаризации

Разложив функцию y=f(x) в ряд Тейлора, получим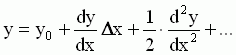



где y₀- значение выхода, соответствующее входу x₀; d^ky/dx^k - значения производных, взятых в точке А(x₀;y₀). Тогда для малых отклонений x:

или 

где  при x=x₀.

Если выходная величина элемента зависит от нескольких входных воздействий, то при линеаризации по методу малых приращений следует определять частные производные по всем воздействиям, а приращение выхода является суммой частных приращений, т.е.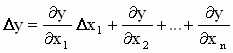

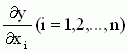 где x₁, x₂, …, x_n - приращения входных воздействий;  - частные производные.

10. 
     Формы записи линейных дифференциальных уравнений. Передаточная функция в операторной форме, передаточная функция в форме изображения Лапласа. Запись дифференциального уравнения через передаточные функции.
    

Линейные ДУ могут быть записаны в естественной, символической и операторной формах.

Естественная форма: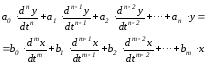

(1.5)

Если производная имеет порядок не выше 2-го, то можно использовать верхние точки в обозначениях производных:  .

Символическая форма:

Производная n-го порядка заменяется символом .

После замены уравнение (1.5) примет более простой вид:

(1.6)

Уравнение, записанное в такой форме, можно преобразовывать как алгебраическое. Однако решение уравнение не упрощается.

Операторная форма:

В основе операторной формы записи уравнения лежит преобразование Лапласа:

Если применить преобразование Лапласа к обеим частям дифференциального уравнения (1.5), то при рулевых начальных условиях для переменных хи у и их производных можно получить следующее операторное уравнение:

(1.7)

Следует обратить внимание формальное совпадение записей в символической (1.6) и операторной (1.7) формах. Однако смысл символа p в операторной и символической формах совершенно различен – если в первой форме p является символом, и вводится исключительно для упрощения записи уравнения, то во втором – это комплексная переменная р, введение которой влечет за собой простой подход к решению уравнения.

Операторная форма записи является основной формой, используемой в теории автоматического управления.

При исследовании и расчете САУ исходят из математического описания, происходящих в них процессах. Для линейных САУ широко используется для этой цели операторный метод. Его сущность в том, что исследуемая система разделяется на звенья направленного действия. Совокупность этих звеньев совместно с линиями связи между ними, характеризующими их взаимодействие, образуют структурную схему САР. Они отражают математически динамические свойства системы. Разбиение системы на звенья существенно облегчает их расчет. Процессы, протекающие в САУ, описываются дифференциальными. уравнениями. Задача составления дифференциальных уравнений системы сводится к составлении системы отдельных звеньев. Любое звено автоматической системы предназначено для измерения, усиления или какого-либо другого преобразования сигнала. В связи с этим для любого элемента характерной являются связи между его входным и выходным сигналом. Именно эта связь и может быть представлена дифференциальными уравнением, которое математически выражает физические процессы в звене, т. е. процессы формирования выходного сигнала элемента, при подаче на его вход входного сигнала. Для облегчения исследования сложных систем дифференциальных уравнений, описывающие поведение системы заменяются алгебраическими, с помощью преобразований Лапласа. Если имеется некоторая функция f(t) независимой вещественной переменной t, то преобразование Лапласа, производимое над этой функцией и обращающее ее в функцию F(x), определяются след соотношением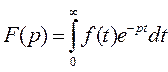



где p-произвольная комплексная величина, имеющая вещественную и мнимую часть. При этом функция f(t) называется оригиналом, а F(p)-изображением функции. Сокращенно преобразования Лапласа обозначаются: 

Для линейных звеньев связь между входным и выходным сигналом может быть описана линейным дифференциальным уравнением следующего вида:



(1)

Воспользовавшись преобразованием Лапласа, дифференциальным уравнением (1) может быть представлено в следующем виде: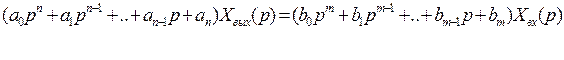



(2)

Левая часть равенства в скобках - выходной операторный полином, правая – входной.

Передаточной функцией звена или системы автоматического управления называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины.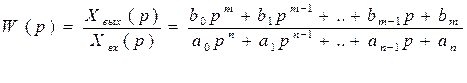



1) При р=0 выражение передаточной функции превращается в коэффициент усиления. W(p)=K.

2) Из выражения передаточной функции видно, что изображение выходной величины равно:



Этим выражением можно пользоваться при определении характера переходных процессов, возникающих в системе, при подаче на ее вход любого произвольно меняющегося входного воздействия. Анализ и синтез систем автоматического управления предполагает предварительное получение информации о виде передаточной функции. Для ряда типовых динамических звеньев передаточные функции являются одинаковыми, отличие может состоять в коэффициенте выражений передаточных функций.

Решение дифференциального уравнения (2.2) можно получить не только классическим методом, но также с использованием операционного исчисления, в основе которого лежит преобразование (интеграл) Лапласа.

Преобразование Лапласа представляет собой преобразование некоторой функции 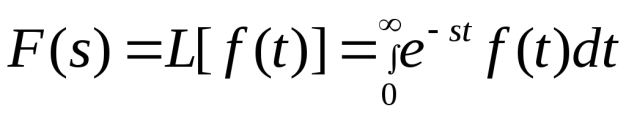  вещественной переменной   в другую функцию  комплексной переменной  , осуществляемое путем интегрирования

,

где исходная функция называется оригиналом, а результат преобразования   – изображением,  – оператор Лапласа.

Существует соответствие между операциями с оригиналами и с изображениями. Так,  -кратному дифференцированию оригинала соответствует умножение изображения  на  , а  -кратному интегрированию оригинала в пределах от 0 до   соответствует деление изображения  на  .

Функция-оригинал обладает следующими свойствами:

• 
   определена и кусочно-дифференцируема на всей положительной числовой оси;
  
• 
  при  ;
  
• 
  существует такое положительное число  , при котором .
  

Для определения функции-оригинала по известному изображению применяют формулу обратного преобразования Лапласа



Максимальная величина  , при которой выполняется это неравенство, называется абсциссой абсолютной сходимости. В АСУ мы обычно имеем дело с функциями, для которых перечисленные выше условия выполняются.

Выражения изображений Лапласа для некоторых элементарных функций приведены в табл.2.1. Более полные таблицы даны в справочной литературе.

Таблица 2.1

Изображения некоторых элементарных функций

Передаточной функцией (в форме изображений Лапласа) называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях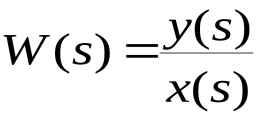

.(2.5)

Введём для операции дифференцирования обозначение  , т.е.  .

В операторной форме уравнение (2.2) имеет вид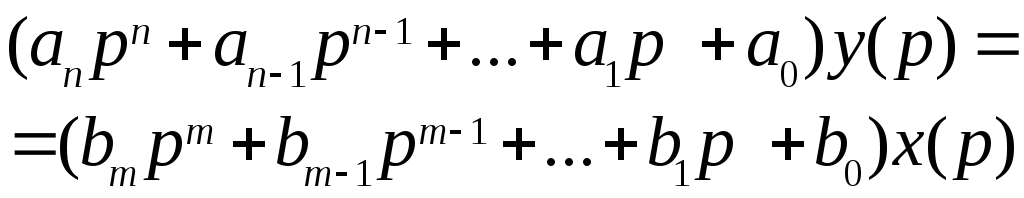

(2.6)

где   – оператор дифференцирования.

Передаточной функцией системы в операторной форме называют отношение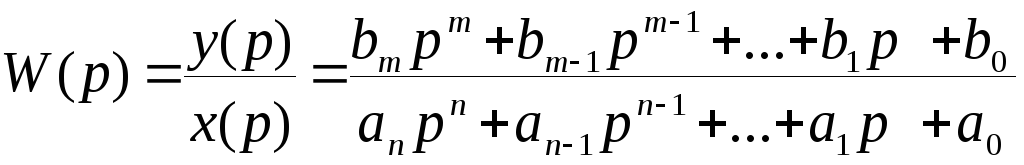

(2.7)

Передаточная функция определяет динамические характеристики системы или отдельных её элементов.

Итак, передаточная функция в форме изображений по Лапласу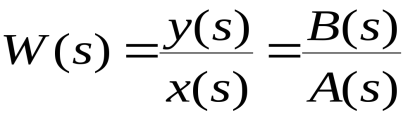

,

гд е ,  – полиномы числителя и знаменателя, характеризует систему в области изображений по Лапласу (рис. 2.12).

Рис.2.12. Модель системы (звена) в области изображений по Лапласу

Для линейных систем при нулевых начальных условиях нет необходимости переходить в область изображений, а систему (звено) можно представить блоком

,

как показано на рис. 2.13, и считать, что этот блок осуществляет те же действия, что предусматриваются дифференциальным уравнением (2.6), записанным в операторной форме

,

т. е.   – операторное звено во временной области.

Ри с.2.13. Модель системы (звена) в операторной форме

Отметим, что (2.7) можно представить в виде отношения полиномов со свободными членами, равными единице

,

где 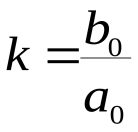  – коэффициент передачи;

;

.

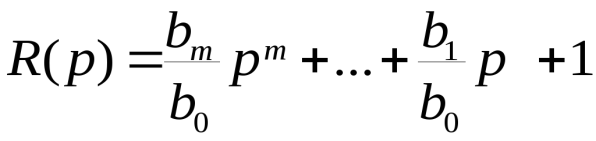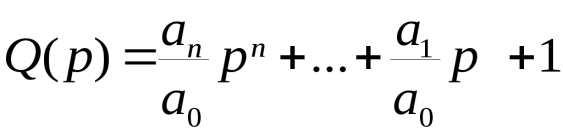Свободные члены могут равняться и нулю, если, например, в системе имеется интегрирующее звено.

Итак, для стационарных линейных звеньев (систем) при нулевых начальных условиях формально можно сделать подстановку  , так как в этом случае дифференцированию оригинала – символическому умножению оригинала на   – соответствует умножение изображения на комплексное число  .

Все свойства преобразования Лапласа применимы для операторной формы записи дифференциальных уравнений линейных стационарных систем при нулевых начальных условиях, т.е. можно для таких систем считать   и тогда выражения (2.5) и (2.7) эквивалентны.

В знаменателе передаточной функции (2.7) записано выражение, аналогичное левой части характеристического уравнения. Поэтому можно считать, что знаменатель передаточной функции есть характеристический полином дифференциального уравнения



Корни характеристического уравнения  , будучи подставленными в (2.7), обращают передаточную функцию в бесконечность и называются полюсами передаточной функции. Корни уравнения   при подстановке в (2.7) обратят передаточную функцию в нуль и называются нулями передаточной функции.