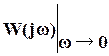ответы на вопросы. ответы на билеты тау. Понятие математического описания автоматических систем управления. Уравнения динамики и статики элементов и систем
 Скачать 1.89 Mb.
|
|
Получение дифференциального уравнения одномерной системы с двумя входами с помощью передаточных функций. Записать дифференциальное уравнение системы управления с одним выходом и двумя входами и , передаточные функции которых имеют вид:
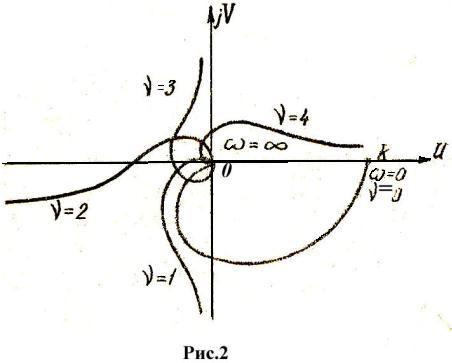
   Решение: Система управления определяется двумя передаточными функциями: 1) передаточной функцией относительно входа :  2) передаточной функцией относительно входа : 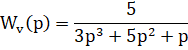 С помощью передаточной функции уравнение рассматриваемой системы управления можно записать в виде: 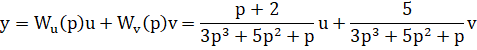 Передаточные функции сложных систем легко могут быть определены через передаточные функции составляющих их элементов. Имеющее наименьший порядок отношение изображений Лапласа выходной и входной переменных, вычисленных при нулевых начальных условиях, называется передаточной функцией в изображениях Лапласа. В соответствии с определением передаточная функция в изображениях Лапласа не может иметь равные между собой нули и полюса, так как в этом случае ее порядок может быть понижен путем сокращения числителя и знаменателя на общий множитель. y = +  y =    y =   Так как оператор , то дифференциальное уравнение системы управления имеет вид:  Амплитудные и фазовые частотные характеристики разомкнутых одноконтурных систем управления. Математическое выражение для передаточной функции разомкнутой системы значительно проще, чем математическое выражение для передаточной функции замкнутой системы. Поэтому в теории автоматического управления во многих случаях оказывается целесообразным рассматривать передаточную функцию разомкнутой системы и по ее свойствам судить о свойствах замкнутой системы. С этой точки зрения большое значение имеет рассмотрение частотных характеристик разомкнутой системы. По аналогии с АФХ звена, АФХ разомкнутой системы получается из выражения для ПФ разомкнутой системы W(p) путем замены р на jw и обозначается W(jw) 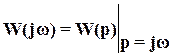 .АФХ разомкнутой системы определяет ее установившуюся реакцию на синусоидальный входной сигнал. Ее математическое выражение может быть представлено в показательной или алгебраической форме:  .Отдельные величины, входящие в это выражение, определяют следующие частотные характеристики разомкнутой системы W(jw)=|W(jw)|'>R(w)=modW(jw)=|W(jw)| - амплитудная частотная характеристика; =argW(jw) – фазовая частотная характеристика; U(w)=ReW(jw) – вещественная частотная характеристика; V(w)=JmW(jw) – мнимая частотная характеристика. АФХ разомкнутой системы строится на комплексной плоскости в координатах U,V при изменении от 0 до ∞ (рис. 1). При отрицательных w АФХ может быть определена из соотношения W(-jw)=W* (jw), аналогично соответствующему соотношению для АФХ звена. Диаграмма Найквиста – годограф W(jw), построенный на комплексной плоскости U,V при изменении от -∞ до ∞. Конкретный вид годографа АФХ можем уточнить, рассмотрев общее выражение для передаточной функции: 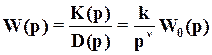 , ,тогда соответствующая ей АФХ будет равна 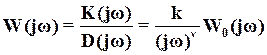 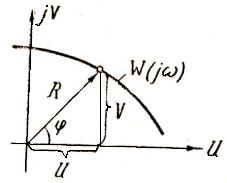 рис. 1 Рассмотрим характер W(jw) при предельных значениях w, равных бесконечности и нулю. При w→∞ 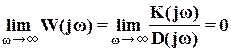 . Это следует из того, что степень многочлена К(р)физически осуществимой системы не превосходит степени многочлена D(p),т.е. degD>degK, и, следовательно, при увеличении w знаменатель выражения для W(jw) растет значительно быстрее, чем числитель.При w→0 поведение АФХ зависит от числа интеграторов. Если ν=0, то  .Если ν≠0, то 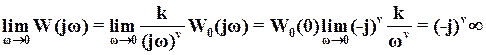 .Значения W(jw) при w → 0 для различных ν удобно задать таблицей. Эта таблица и графики АФХ разомкнутой системы для различных значений ν приведены на рис. 2.
 Логарифмические амплитудные и фазовые частотные характеристики разомкнутых систем. Правила построения асимптотических ЛАЧХ. Логарифмической амплитудной частотной характеристикой (ЛАЧХ) называется график зависимости L(w)=20lgR(w), построенный в логарифмическом масштабе частот (lgw). Логарифмической фазовой частотной характеристикой (ЛФЧХ) называется график φ(w), построенный в логарифмическом масштабе частот (lgw). Выражение L(w)=20lgR(w) есть амплитудно-частотная характеристика разомкнутой системы, выраженная в децибелах. Фазово-частотную характеристику φ(w) будем выражать в градусах или в радианах. Рассмотрим вопрос о построении логарифмических частотных характеристик разомкнутой системы. Часто осуществляют декомпозицию ПФ разомкнутой системы, т.е. представляют ее в виде произведения ПФ типовых динамических звеньев. В качестве таких звеньев принимают: А) Форсирующее звено второго порядка с ПФ  ,Б) Форсирующее звено первого порядка с ПФ W(p)=Tp+1, В) Апериодическое звено с ПФ W(p)=(Tp+1)-1, Г) Колебательное звено с ПФ  .При этом ПФ разомкнутой системы 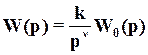 состоит из сомножителей типа двучленов Тр+1 и квадратичных трехчленов  , расположенных в числителе или знаменателе этой ПФ, а также из сомножителя k/pν.Очевидно, что сомножителю в знаменателе соответствуют апериодическое или колебательное звено, сомножителю, стоящему в числителе соответствует форсирующее звено первого или второго порядка. Обозначим сомножитель ПФ через Wk(p). Тогда ПФ разомкнутой системы, включающая n сомножителей, может быть записана в виде 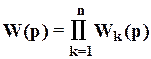 .Полагая p=jw, получим выражение АФХ разомкнутой системы: 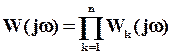 .Логарифмическая амплитудно-частотная характеристика равна 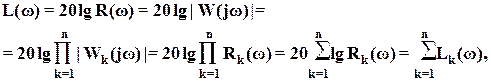 где  представляет собой ЛАЧХ отдельного сомножителя.Следовательно, ЛАЧХ разомкнутой системы равна алгебраической сумме логарифмических частотных характеристик отдельных сомножителей передаточной функции, причем отдельные слагаемые берутся со знаком «+» или « - » в зависимости от того, где стоит соответствующий сомножитель: в числителе или знаменателе передаточной функции. Фазовая частотная характеристика разомкнутой системы равна 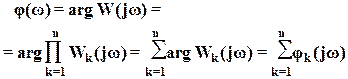 ,где  .Как видно, фазовая частотная характеристика разомкнутой системы равна сумме фазовых частотных характеристик отдельных сомножителей передаточной функции, взятых со знаком «+» или « - » в зависимости от того, стоит ли соответствующий сомножитель в числителе или знаменателе передаточной функции. Таким образом, для построения вручную логарифмических частотных характеристик системы необходимо построить логарифмические частотные характеристики для отдельных сомножителей передаточной функции и сложить их алгебраически. Часто модель объекта управления представляет собой последовательную цепочку типовых звеньев, поэтому можно получить, суммируя отдельные ЛАЧХ. Подобное суммирование позволяет предложить следующую процедуру построения . На частоте (или в логарифмическом масштабе ) фиксируется точка, соответствующая значению  , где – коэффициент усиления объекта.На оси абсцисс отмечаются частоты сопряжения (или  ), , где n – число типовых звеньев в составе передаточной функции объекта.До первой частоты сопряжения строится низкочастотная асимптота с наклоном дБ/дек., если  содержит интегрирующие звенья, а r – число таких звеньев. Наклон характеристики будет равен дБ/дек., если передаточная функция объекта содержит дифференцирующие звенья, l – число этих звеньев. Низкочастотная асимптота строится таким образом, чтобы она сама или ее продолжение проходили через точку .На частотах сопряжения происходит «излом» асимптотической ЛАЧХ объекта. Наклон ЛАЧХ изменяется на дБ/дек., если соответствующая частоте сопряжения постоянная времени находится в знаменателе передаточной функции объекта, r – число таких звеньев. «Излом» асимптотической ЛАЧХ будет равен дБ/дек., если постоянная времени находится в числителе передаточной функции, l – число звеньев. Новая асимптота проводится до следующей частоты сопряжения, где также происходит ее «излом» в соответствии с указанным правилом. |
