зачет. Зачет. Представление сигналов ортогональными функциями (цель, сущность, примеры с приведением временных диаграмм)

• Название: Представление сигналов ортогональными функциями (цель, сущность, примеры с приведением временных диаграмм)
• Анкор: зачет
• Дата: 01.09.2022
• Размер: 333.5 Kb.
• Имя файла: Зачет.doc
• Тип: Документы; #658959

Билет №4.

1. 
   Представление сигналов ортогональными функциями (цель, сущность, примеры с приведением временных диаграмм).
   

Сущность большинства задач анализа реальных сигналов заключается в том, чтобы эти сигналы, которые в большинстве случаев являются сложными, представить в виде совокупности простых элементарных сигналов, удобном для последующего анализа их прохождения через те или иные цепи. Например, реальный сигнал может быть представлен в виде суммы ортогональных составляющих (элементарных сигналов): , , (1.1)

Интервал показывает время действия сигнала. Так как система ортогональных функций, применяемая для разложения заранее известна, то сигнал полностью определяется набором весовых коэффициентов для этих функций. При приближенном представлении сигналов, набор чисел всегда конечен. Такие наборы чисел называют спектрами сигналов.

Спектры являются удобной аналитической формой представления сигналов в рамках линейной теории. Основная задача – правильный выбор системы ортогональных функций (базиса), удобной для последующего анализа прохождения сигнала через те или иные цепи и каналы связи.

При решении практических задач приходится учитывать в (1.1) ко­нечное число N членов. При этом заданная функция s(t) будет пред­ставлена приближенной функцией; , (1.2)

Базисные функции , k = 0,1,..., N-1, выбираются исходя из ап­риорной информации об исследуемом сигнале так, чтобы они имели бо­лее простое аналитическое выражение, обеспечивали быструю сходи­мость ряда (1.2) и позволяли легко вычислять значения коэффициентов , k = 0,1,..., N-1

Коэффициенты , k =0,1,2, ...,N-1 рассчитываются из условия, чтобы некоторый заранее выбранный критерий приближения принимал минимальное значение. Приведем критерии приближения, получившие наибольшее распространение.

1. 
   В качестве меры расхождения исходной s(t) и аппроксимирую­щей функций принимается минимум среднеквадратической по­грешности
   

(1.3)

Такая аппроксимация называется приближением в среднеквадра­тическом.

2.Можно потребовать, чтобы максимальное значение погрешности аппроксимации было минимальным на заданном интервале определения функции s(t). Такое приближение называется равномерным приближением.

3.Если в качестве меры приближения выбрать среднюю погреш­ность

,то говорят, что имеет место приближение в среднем.

Чаще всего в качестве критерия приближения используется квадра­тичный критерий вида (1.3). Запишем его в следующем виде

Для детерминированных сигналов большое распространение получили методы спектрального анализа, использующие преобразования Фурье. Представление сигнала  гармоническими функциями имеет следующие преимущества: простое математическое описание; инвариантность к линейным преобразованиям, т. е. если на входе линейной цепи действует гармоническое колебание, то и на выходе ее также будет гармоническое колебание, отличающееся от входного только амплитудой и начальной фазой; как и сигнал, гармонические функции периодические и имеют бесконечную длительность; техника генерирования гармонических функций достаточно проста. Если разложение входного сигнала по ортогональной системе тригонометрических функций известно, то выходной сигнал может быть получен как сумма независимо преобразованных цепью входных гармоник. В этих методах в роли выступают гармонические функции, а роль коэффициентов играют амплитуды гармоник. Для случайных сигналов наибольшее распространение получили методы корреляционного и спектрального анализа, основанные на преобразовании Хинчина-Винера. Эти преобразования являются результатом распространения метода Фурье на случайные процессы. При разложении случайных процессов коэффициенты являются случайными величинами, а оптимальные базисы определяются через корреляционные функции этих процессов.

К системе базисных функций предъявляются следующие основные требования: для любого сигнала ряд должен сходиться, функции должны иметь простую аналитическую форму, коэффициенты должны вычисляться относительно просто.

Этим трем условиям удовлетворяют системы ортогональных функций. Условие ортогональности функций на интервале 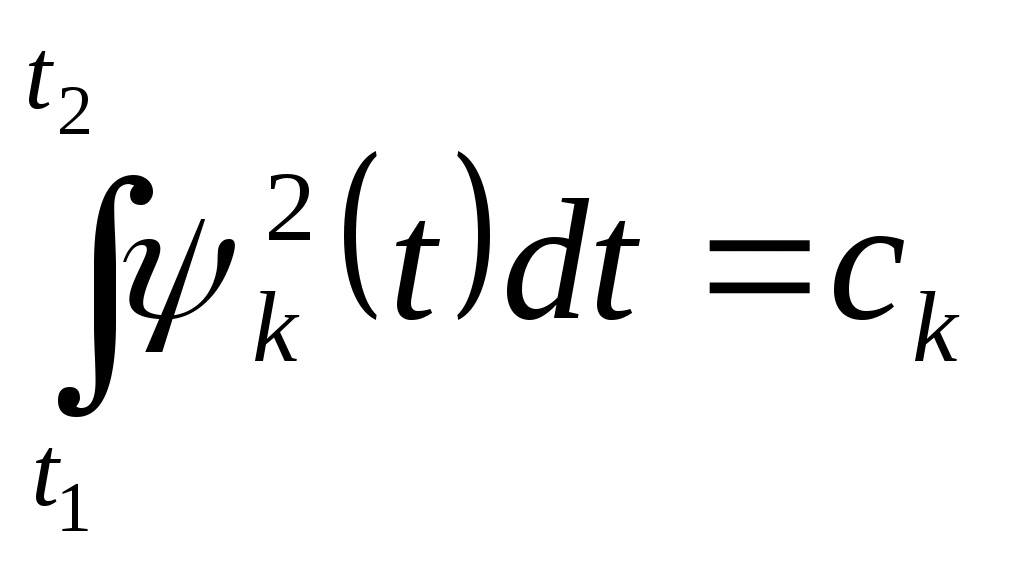имеет вид:

, . При

Число называют нормой базисной функции .

Каждую базисную функцию можно пронормировать по ее норме, тогда нормированная базисная функция: .

Новая система 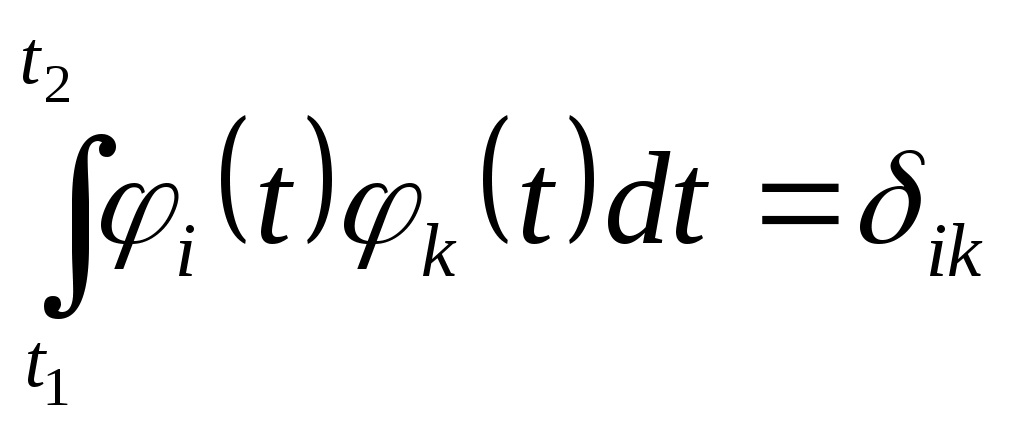удовлетворяет не только условию ортогональности, но и условию нормировки, которое имеет вид:

, где

- символ Кронекера. Систему называют ортонормированной.
Определим коэффициенты, 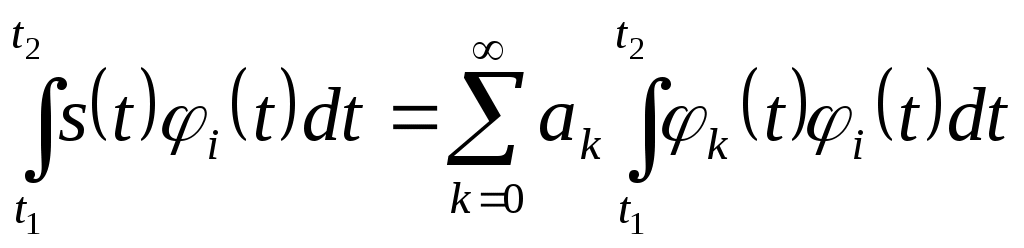разложив сигнал по системе ортонормированных функций. Для этого умножим обе части уравнения на и проинтегрируем на интервале . В результате получим: .

Из условия ортонормированности следует, что в правой части полученного уравнения все интегралы при 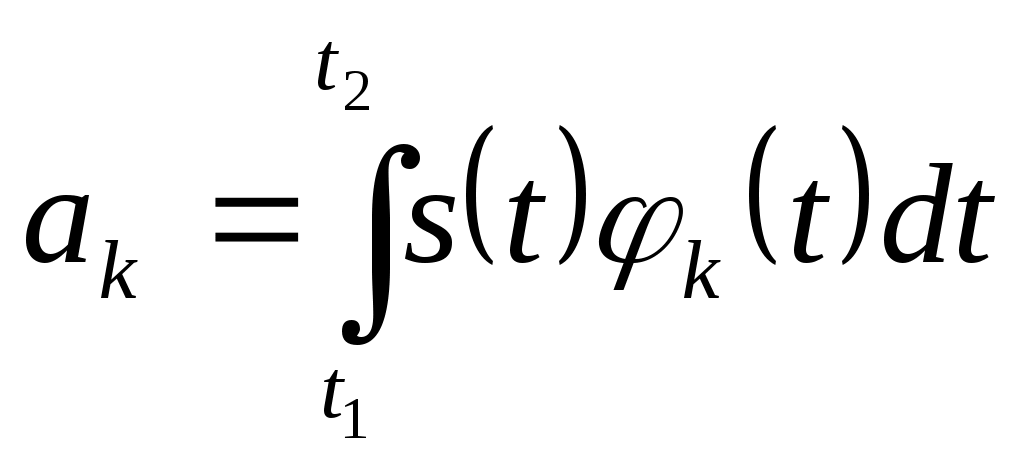будут равны нулю, а при один интеграл равен единице, значит: .

Ортогональное разложение называют обобщенным рядом Фурье, а коэффициенты – обобщенными коэффициентами Фурье. Ортонормированные функции удовлетворяют всем трем указанным выше условиям.

Для того чтобы по выбранной базисной системе функций можно было разложить любой сигнал из заданного множества, необходимо, чтобы система была полной. Система ортогональных функций называ­ется полной, если к ней нельзя добавить ни одной новой функции, кото­рая была бы ортогональна ко всем другим функциям этой системы. Ес­ли система ортогональных функций является неполной, то по ней нельзя разложить любой сигнал (в частности сигнал, который совпадает с ортогональной функцией, отсутствующей в системе).

Методы представления сигналов в виде (1.2) составляют основу обобщенной спектральной теории сигналов. Обобщенная спектральная теория исследует общие закономерности спектрального анализа для различных систем базисных функций и рассматривает особенности вы­бора базисных систем при решении задач передачи и обработки сигна­лов.

Для разложения сигналов можно использовать многие разработан­ные к настоящему времени системы базисных функций, такие как три­гонометрические функции, полиномы Эрмита, Лежандра, Чебышева, функции Бесселя, Лагерра, Уолша, Хаара и другие. При выборе системы базисных функций необходимо выполнить следующие требования:

1. 
   область определения сигналов и базисной системы должна быть одна и та же;
   
2. 
   базисная система должна быть линейно независимой;
   
3. 
   базисная система должна быть полной, а образующие ее функ­ции - ортогональными;
   
4. 
   базисные функции должны иметь конечную энергию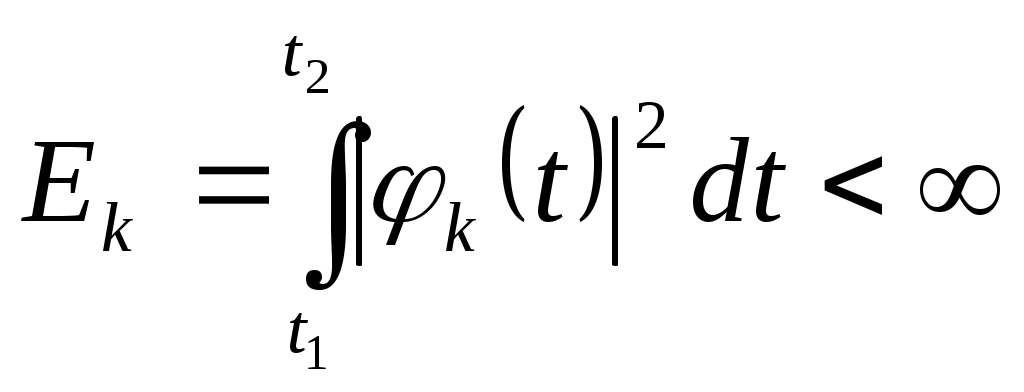
   

Обычно для анализа сигналов рекомендуют выбирать систему ба­зисных функций, обеспечивающую наиболее быструю сходимость ряда (1.2), то есть требующую наименьшего числа членов ряда для заданной точности представления сигнала. В ряде случаев решающим при выборе системы функций является простота физического генерирования базис­ных функций, образующих систему.


Рисунок 1.
На рис.1 приведена система функций Хаара, ортонормированность которых на интервале 0-1 также очевидна. Известны представления сигналов по системам ортогональных базисных многочленов Котельникова, Чебышева, Лаггера, Лежандра и др., а также неортогональные разложения по функциям Лагранжа, Тейлора и др.
Рассмотрим в качестве примера корреляционный приемник.
Корреляционный приемник обнаруживает и идентифицирует сигнал, сравнивая его с опорным сигналом. Сравнение осуществляется вычислением коэффициента взаимной корреляции  принятого s(t) и опорного s_оп(t) сигналов за время передачи одного символа Т_s: где E_s –энергия сигнала, соответствующего одному символу.

В общем случае коэффициент корреляции может принимать значения от +1 при идентичных сигналах до -1 при противоположных (антиподных) сигналах. Сигналы, для которых  = 0, называются ортогональными. Примеры противоположных сигналов s₁(t), s₂(t):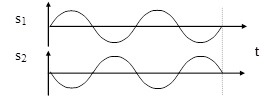



В качестве опорного сигнала достаточно взять один из этих сигналов, например, s₁(t). При приеме сигнала s₁(t) или s₂(t) на выходе корреляционного приемника будет получен сигнал положительной или отрицательной полярности соответственно.

2. 
   Рекурсивные цифровые фильтры: разностное уравнение, схема алгоритма, сигнал на выходе.
   

Конструкция РЦФ отображается в z-образе передаточной функции фильтра в виде отношения двух многочленов:

H(z) = H₀+H₁z+H₂z²+...= B(z)/[1+A(z)], (2.1)

где: B(z) = B₀+B₁z+B₂z²+ ... +B_Nz^N, A(z) = A₁z+A₂z²+ ... +A_Mz^M.

Естественно, что переход на РЦФ имеет смысл только в том случае, если степень многочленов A(z) и B(z) во много раз меньше степени многочлена H(z) прямого z-преобразования импульсной реакции фильтра. При z-образе входных данных Х(z), на выходе РЦФ имеем:

Y(z) = H(z)Х(z) = X(z)B(z)/[1+A(z)],

Y(z)[1+A(z)] = Y(z)+Y(z)A(z) = X(z)B(z),

Y(z) = X(z)B(z)-Y(z)A(z). (2.2)

При обратном z-преобразовании выражения (2.2) получаем уравнение рекурсивной цифровой фильтрации:

y_k = b_n x_k-n – a_m y_k-m. (2.3)


Рис. 2.1
Рекурсивная фильтрация требует задания начальных условий как по x_k, так и по y_k при k<0. Схема рекурсивной фильтрации приведена на рис. 2.1.
Как следует из выражения (2.3), при вычислении значения у_k текущей точки используются предыдущие вычисленные значения y_k-m, (m>0), что и определяет принцип рекурсии - фильтрации с обратной связью. Другой особенностью РЦФ является их односторонность, и физическая реализуемость в реальном масштабе времени. При машинной обработке данных многочлен B(z) передаточной функции фильтра может реализоваться и в двухстороннем варианте.

Одно из важнейших свойств рекурсивных фильтров - возможность получения узких переходных зон при конструировании частотных фильтров, так как функция H(z) фильтра может резко изменяться при приближении к нулю многочлена в знаменателе (2.1).

Рекурсивная фильтрация требует более высокой точности вычислений по сравнению с нерекурсивной, т.к. использование предыдущих выходных отсчетов для текущих вычислений может приводить к накапливанию ошибок. Особое значение это имеет для фильтров с передаточными функциями высоких порядков (M>3), которые чувствительны к эффектам конечной разрядности. Такие фильтры, как правило, разбиваются на фрагменты – звенья второго и/или первого порядка, и реализуются в каскадной или в параллельной форме.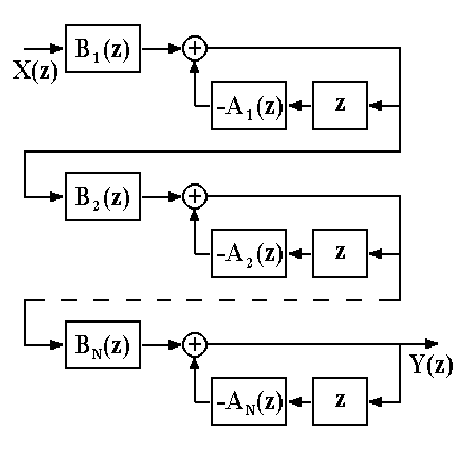




Рис. 2.2. Каскадная форма.
Каскадная форма. Находятся корни многочленов А(z), B(z) и производится разложение H(z):

H(z) = , (2.4)

где G - масштабный множитель. Это позволяет применять каскадное построение фильтров, показанное на рис. 9.1.2, в котором:

H(z) = G H₁(z) H₂(z) ..... H_N(z),

(2.5)

Функции А_n(z) и B_n(z) обычно представляются в виде биквадратных блоков (фильтров второго порядка):

B_n(z) = b_n0 + b_n1 z + b_n2 z², A_n(z) = 1 + a_n1 z + a_n2 z².

В принципе, порядок расположения блоков в каскадной форме, равно как и порядок множителей B(z) и A(z) в числителе и знаменателе функции (2.4), значения не имеет. Однако следует учитывать, что полюса знаменателя, близкие к единичной окружности на z-плоскости (близкие по модулю к 1) формируют большие коэффициенты усиления на соответствующих частотах в блоках, в которых они находятся, и при обработке сигналов могут вызывать переполнение разрядов числовых ячеек этих блоков, если их разрядность ограничена. С учетом этого при формировании каскадов желательно объединять в пары нули и полюса, близкие по модулю к 1, и располагать их в концевые блоки каскадной формы. Такое комбинирование полезно также с позиций наилучшего отношения сигнал/шум.




Рис. 2.3.
Параллельная форма. Функция H(z) разлагается на элементарные дроби:

,

что дает параллельную форму фильтра, показанную на рис. 2.3. Параллельная конструкция фильтра применяется реже каскадной, хотя это может объясняться и тем, что в аналоговых фильтрах, исторически предшествовавших цифровым фильтрам, теоретическая база анализа и синтеза каскадных рекурсивных фильтров получила детальное развитие.

Стандартные блоки рекурсивных фильтров обычно реализуются биквадратными звеньями в канонической форме, которая имеет минимальное количество элементов задержки. Уравнения звена: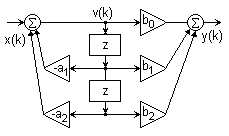




Рис. 2.4
v(k) = x(k) – a(n) v(k-n), y(k) = b(n) v(k-n). (2.6)

Функциональная схема реализации звена приведена на рис. 2.4.

Вторая форма реализации – по уравнению (2.5) в прямой форме, приведенная на рис. 2.5:

y(k) = 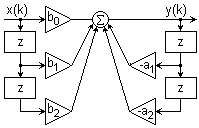b(n) x(k-n) – a(n) y(k-n). (2.7)


Рис. 2.5
При определенных условиях прямая форма лучше канонической с точки зрения шумовых характеристик.

При нулевых значениях коэффициентов a₂ и b₂ звенья второго порядка превращаются в звенья первого порядка.

Устранение сдвига фазы. Рекурсивные фильтры являются фазосдвигающими фильтрами. Если требуется обеспечить нулевой фазовый сдвиг, то операция фильтрации производится дважды, в прямом и обратном направлении числовой последовательности массива данных, при этом амплитудно-частотная характеристика (АЧХ) фильтрации будет равна |H(z)|² фильтра, что необходимо учитывать при конструировании фильтра.

3. 
   Качественно построить графики спектра периодической последовательности прямоугольных импульсов со скважностью 2; 2,7; 3 (один под другим). Дать необходимые пояснения вида графиков.
   

Разложим в ряд Фурье периодическую последовательность прямоугольных видеоимпульсов с известными параметрами (рис. 3.1.), четную относительно точки t=0:





Рис.3.1. Временное представление периодической последовательности прямоугольных импульсов.
Воспользуемся для представления этого сигнала формой записи ряда Фурье в виде (3.1.). Для спектрального представления последовательности прямоугольных импульсов начало отсчета целесообразно брать в середине импульса. Действительно, в этом случае и в разложении останутся только косинусоидальные составляющие, так как интегралы от нечетных функций за период равны нулю b_k=0.

Коэффициенты Фурье: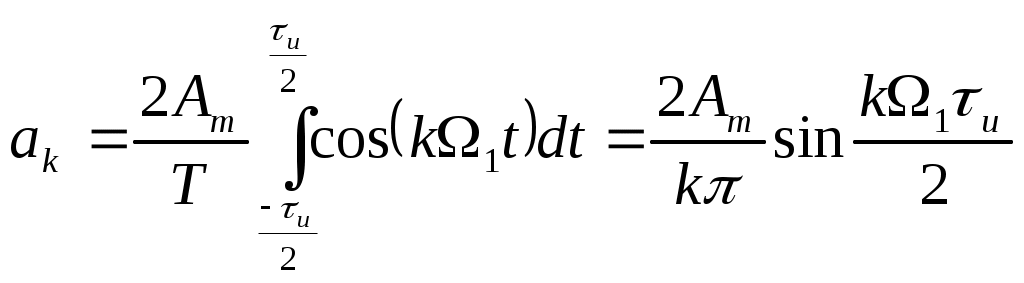



 

позволяющие записать ряд Фурье:



где  - скважность импульсной последовательности.

Для построения спектральных диаграмм при конкретных числовых данных полагаем  k=0,1,2,3,…и вычисляем коэффициенты гармоник. Результаты расчета первых восьми составляющих спектра при  ,  ,   сведены в табл. 1.1 и построены спектральные диаграммы на рис. 3.2.

 

Таблица 1.1. Амплитуды спектральных составляющих для периодической последовательности прямоугольных импульсов

k		0	1	2	2,7	3	4	5	5,4	6	7	8	9
k, Гц		0	50	100	135	150	200	250	270	300	350	400	450
ak, В	S=2	1	1,27	0	0,42	0,425	0,25	0	0,13	0	0,18	0	0
	S=2,7	0,74	1,17	0,46	0	0,15	0,32	0,12	0	0,14	0,17	0,02	0
	S=3	0,67	1,10	0,55	0,15	0	0,28	0,22	0,14	0	0,16	0,14	0

Рис. 3.2. Спектральные диаграммы периодической последовательности импульсов: при скважности S=2, S=2,7,S=3

Линия, построенная по формуле  , называется огибающей спектра амплитуд, в которую вписываются амплитуды гармоник на своих частотах  . Нули огибающей будут на тех частотах, на которых
  , где (n = 1, 2, 3, …),

откуда  . Постоянная составляющая определяется как  .
Из приведенного примера следует, что с увеличением скважности увеличивается число спектральных составляющих и уменьшаются их амплитуды.

Выбор количества спектральных составляющих зависит от формы сигнала и точности его представления рядом Фурье. Плавное изменение формы сигнала потребует меньше числа гармоник при той же точности представления, чем для скачкообразного сигнала. Для приближенного представления прямоугольных импульсов на практике обычно считают, что достаточно трех - пяти гармоник.