Лекция 2 Математические модели и их классификации Математическая модель
 Скачать 153.52 Kb. Скачать 153.52 Kb.
|
|
Лекция 2 Математические модели и их классификации 2.1. Математическая модель Понятие «математическое моделирование» в последние несколько десятилетий является достаточно рас‑пространенным в научной литературе, в частности, в естественнонаучной и технической. В настоящее время практически на любом проектном или конструкторском предприятии применяются математические модели. В последние годы широкое распространение получило применение математического моделирования в научных исследованиях, особенно в таких областях, как экономика, управление, история, биология и др. Следует заметить, что математическое моделирование представляет собой отдельную междисциплинарную область знаний с совокупностью объектов, подходов и методов исследования. Математической моделью называется совокупность уравнений или других математических соотношений, отражающих основные свойства изучаемого объекта или явления в рамках принятой умозрительной физической модели и особенности его взаимодействия с окружающей средой на пространственновременных границах области его локализации. Математические модели различных процессов в континуальных системах строятся, как правило, на языке дифференциальных уравнений, позволяющих наиболее точно описать состояние процесса в любой точке пространства в произвольный момент времени. Основными свойствами математических моделей являются адекватность и простота, указывающие на степень соответствия модели изучаемому объекту и возможности ее реализации. Процесс формулировки математической модели называется постановкой задачи. Под математическим моделированием можно понимать процесс построения и изучения математических моделей. Развернутое определение дано в работе: математическое моделирование — это идеальное научное знаковое формальное моделирование, при котором описание объекта осуществляется на языке математики, а исследование модели проводится с использованием тех или иных математических методов. 2.2. Обобщенная математическая модель Математическая модель описывает зависимость между исходными данными и искомыми величинами. Элементами обобщенной математической модели являются: множество входных данных (переменные) X, Y; X — совокупность варьируемых переменных; Y — независимые переменные (константы); математический оператор L, определяющий операции над этими данными, под которым понимается полная система математических операций, описывающих численные или логические соотношения между множествами входных и выходных данных (переменные); множество выходных данных (переменных) G (X, Y); представляет собой совокупность критериальных функций, включающую (при необходимости) целевую функцию. Математическая модель является математическим аналогом проектируемого объекта. Степень адекватности ее объекту определяется постановкой и корректностью решений задачи проектирования. Множество варьируемых параметров (переменных) X образует пространство варьируемых параметров Rx (пространство поиска), которое является метрическим с размерностью n, равной числу варьируемых параметров. Множество независимых переменных Y образуют метрическое пространство входных данных Ry. В том случае, когда каждый компонент пространства Ry задается диапазоном возможных значений, множество независимых переменных отображается некоторым ограниченным подпространством пространства Ry. Множество независимых переменных Y определяет среду функционирования объекта, т. е. внешние условия, в которых будет работать проектируемый объект. Это могут быть: технические параметры объекта, не подлежащие изменению в процессе проектирования; физические возмущения среды, с которой взаимодействует объект проектирования; тактические параметры, которые должен достигать объект проектирования. Выходные данные рассматриваемой обобщенной модели образуют метрическое пространство критериальных показателей RG. 2.3. Нелинейность математических моделей Простота моделей во многом связана с их линейностью. С точки зрения математики это соответствует принципу суперпозиции, при котором любая линейная комбинация решений в свою очередь тоже есть решение искомой задачи. Пользуясь принципом суперпозиции, можно, найдя решение в каком‑либо частном случае, построить решение в более общей ситуации. В этой связи о закономерностях общего случая делается вывод на основе свойств частного. Для линейных моделей отклик объекта на изменение каких‑то условий пропорционален величине этого изменения. В случае отсутствия выполнения принципа суперпозиции для математических моделей знание о поведении части объекта нелинейного явления не дает информации о поведении всего объекта в целом. Большинство реальных процессов и соответствующих им математических моделей не линейны. Линейные модели являются неким приближением реального объекта и решают лишь частные случаи. Так, нелинейными становятся модели популяций при учете ограничения доступных ресурсов. 2.4. Степень соответствия математической модели объекту Математическая модель никогда не бывает тождественна рассматриваемому объекту и не передает всех его свойств и особенностей. Она является лишь приближенным описанием объекта и носит всегда приближенный характер. Точность соответствия определяется степенью соответствия адекватности модели и объекта. При построении математической модели приходится выдвигать дополнительные предположения — гипотезы. Модель поэтому еще называют гипотетической. Основным критерием применимости модели является эксперимент. Критерий практики позволяет сравнивать гипотетические модели и выбирать из них наиболее подходящую. Каждый объект описывается ограниченным числом моделей или их систем. Процесс моделирования значительно легче реализуется при использовании унификации математических моделей, т. е. использования наборов готовых моделей. Существует возможность переноса готовых моделей из одних процессов на другие, идентичные, аналогичные. Аналогичными называют объекты и процессы, описываемые одинаковыми по форме уравнениями, содержащими различные физические величины и параметры, связанные между собой одинаковыми операторами. Величины, которые в аналогичных уравнениях стоят на одинаковых местах, называют аналогами. Математическая модель описывает реальный объект с каким то приближением. Степень соответствия описания реальному процессу определяется полнотой учета возмущающих воздействий. При отсутствии или незначительности возмущений, действующих как внутри, так и вне объекта, можно однозначно определить влияние входных и управляющих параметров на выходные. 2.5. Классификация математических моделей В настоящее время существует огромное количество моделей самого разного типа, которые получили развитие в результате применения методов математического моделирования в различных областях. В связи с этим возникает необходимость в определенной классификации существующих и появляющихся математических моделей. Существуют следующие виды классификаций математических моделей в зависимости от: сложности объекта моделирования; оператора модели; входных и выходных параметров; цели моделирования; способа исследования модели; объектов исследования; принадлежности модели к иерархическому уровню описания объекта; характера отображаемых свойств; порядка расчета; использования управления процессом. По сложности объекта исследования модели делятся на простые и исследующие объекты‑системы (рис. 7). В простых моделях внутреннее строение объекта не рассматривается и составляющие его элементы и подпроцессы не учитываются. Объект‑система является совокупностью взаимосвязанных элементов, которые взаимодействуют с окружающей средой как с единым целым.  Рис. 7 Классификация математических моделей по сложности объекта В зависимости от оператора модели они делятся на линейные, нелинейные, алгоритмические, простые и сложные (см. рис. 8). При наличии линейной зависимости выходных параметров от входных математическая модель называются линейной, соответственно в случае нелинейной зависимости модель — нелинейная. При обеспечении оператором модели функциональной зависимости выходных параметров от входных в виде алгебраического выражения модель является простой. Модель, включающая системы дифференциальных и интегральных соотношений, называется сложной. В случае построения имитатора модели поведения объекта с помощью алгоритма его называют оператором модели. При этом сама модель является алгоритмической.  Рис. 8 Классификация математических моделей в зависимости от оператора модели Классификация математических моделей в зависимости от входных и выходных параметров представлена на рис. 9. По характеру моделируемого процесса модели подразделяются на: детерминированные, которые соответствуют детерминированным процессам, имеющим строго однозначную связь между физическими величинами, характеризующими состояние системы в какой‑либо момент времени; детерминированная модель позволяет однозначно вычислить и предсказать значения выходных величин по значениям входных параметров и управляющих воздействий; неопределенные, которые исходят из того, что изменение определяющих величин происходит случайным образом и значения выходных величин находятся в вероятностном соответствии с входными величинами и не определяются однозначно. 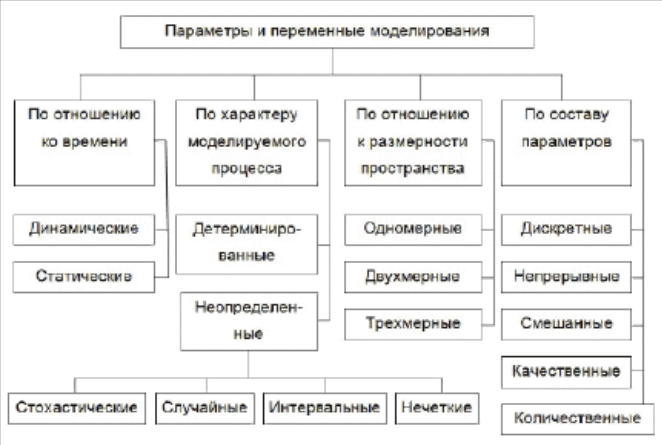 Рис. 9 Классификация математических моделей в зависимости от входных и выходных параметров Модели с неопределенными параметрами можно подразделить на следующие группы: Стохастические — значения всех или отдельных параметров модели определяются случайными величинами, заданными плотностями вероятности. Случайные — значения всех или отдельных параметров модели определяются случайными величинами, которые зависят от оценки плотностей вероятности, определяемой в результате обработки ограниченной экспериментальной выборки данных параметров. Интервальные — значения всех или отдельных параметров модели описываются интервальными величинами, заданным интервалом, образованным минимальными и максимально возможными значениями параметра. Нечеткие — значения всех или отдельных параметров модели описываются функциями принадлежности соответствующему нечеткому множеству. Модели по отношению к размерности пространства классифицируются на одномерные, двухмерные и трехмерные. Такое разделение применимо для моделей, имеющих в качестве параметров координаты пространства. По отношению ко времени модели делят на динамические и статические. Некоторые характеристики моделей являются неизменными, т. е. не меняют своих значений в течение времени, а некоторые изменяются по определенным законам. Если состояние системы меняется со временем, то модели называют динамическими, в противном случае — статическими. Статическое моделирование служит для описания состояния объекта в фиксированный момент времени, а динамическое — для исследования объекта во времени. Разделение моделей на качественные и количественные, дискретные и непрерывные, а также на смешанные происходит в зависимости от вида используемых множеств параметров модели. По целям моделирования модели делятся на дескриптивные, оптимизационные и управленческие (см. рис. 10). Среди целей дескриптивных моделей можно выделить установление законов изменения параметров модели. Примером данной модели является модель движения ракеты после запуска. С помощью оптимизационных моделей можно рассчитывать оптимальные критерии параметров объекта моделирования. С другой стороны, данные модели могут применяться для поиска оптимального режима управления процессом. К оптимизационным моделям можно отнести модель ракеты из предыдущей модели с целью подъема на необходимую высоту за ограниченное время.  Рис. 10 Классификация математических моделей в зависимости от целей моделирования С целью принятия эффективных управленческих решений в областях жизнедеятельности человека применяются управленческие модели. В зависимости от метода реализации модели делят на аналитические, если возможно получить выходные параметры в виде аналитических выражений, и на алгоритмические, позволяющие получить лишь приближенные значения искомых параметров (рис. 11).  Рис. 11 Классификация математических моделей в зависимости от метода реализации модели По объектам исследования математические модели классифицируют на: объекты с высокой степенью информации, если в прoцессе моделирования известны полные системы уравнений, описывающие все стороны моделируемого процесса и все числовые значения параметров этих уравнений; ·объекты с нулевым уровнем информации; математическая модель такого объекта строится на основе статистических экспериментальных данных; объекты с известными основными закономерностями; значения констант в математических уравнениях описания модели устанавливают из опыта; объекты, о поведении которых имеются сведения эмпирического характера; для них используют методы физического моделирования с применением математического планирования эксперимента. По принадлежности модели к иерархическому уровню описания объекта. Иерархический уровень включает: микроуровень (типовыми процессами являются массообменные, теплофизические, гидродинамические), моделирование осуществляется в целях синтеза технологического процесса для отдельного или нескольких агрегатов; макроуровень — моделирование процессов, имеющих бoлее высокий уровень агрегации; модели применяют для синтеза текущего управления технологическим процессом для одного агрегата или технологического комплекса в целом; метауровень — моделирование процессов в совокупности агрегатов и связывающих их материально‑энергетических потоков; такие модели служат для синтеза технологического комплекса как единого целого, то есть для синтеза управления развитием. По характеру отображаемых свойств модели подразделяют на: функциональные модели, используемые для описания физических и информационных процессов, протекающих при функционировании объекта; структурные, описывающие состав и взаимосвязи элементов системы (процесса, объекта). Классификация математических моделей по порядку расчета. Подразделяют на прямые, обратные, индуктивные: прямые применяются для определения кинетических, статических и динамических закономерностей процессов; обратные (инверсионные) используются для определения, например, допустимых отклонений режимов обработки; индуктивные применяются для уточнения математических уравнений кинетики, статики или динамики процессов с использованием новых гипотез или теорий. Специфические особенности всех видов моделей отражаются, прежде всего, в задании и форме начальных и граничных условий. В прямых моделях кинетические закономерности характеризуют течение процесса во времени и устанавливают изменение во времени его параметров: концентраций, температур, химического состава при известных потоках и параметрах рабочих тел. Статические закономерности определяют конечные критические и равновесные значения параметров процесса и рабочего компонента. Уравнения статики получают в основном при обработке экспериментальных данных. Динамические закономерности определяют свойства объектов при разработке систем автоматического регулирования. Динамические свойства задаются характером выходной реакции объекта на стандартные возмущения на входе. Под стандартными возмущениями в химической технологии подразумевают, например, изменение концентрации, давления, температуры и др. Решение приме‑ няемой в модели системы дифференциальных уравнений представляется в виде отношения изображения выходного сигнала к изображению входного сигнала, которое называется передаточной функцией. Обратные (инверсные) модели применяют для определения значения входных параметров или других заданных свойств обрабатываемых веществ или продуктов, а также для определения допустимых отклонений режимов обработки, не оказывающих существенного влияния на качество продукта или показатели процесса. При определении входных параметров исходят из продолжительности процесса, заданных величин конечных параметров или оптимальных свойств выходных продуктов (химического состава, физических свойств и др.). Обратные модели применяют для моделирования кинетических, статических и динамических обратных задач. Как правило, обратными задачами являются задачи оптимизации процессов и параметров аппаратов. Индуктивные модели необходимы для установления или уточнения математических уравнений кинетики, статики и динамики процессов и чаще всего реализуются экспериментально или аналитически с использованием новых гипотез, форм описания или теорий с последующей проверкой адекватности математического описания. Адекватность математического описания в регрессионных моделях оценивается сопоставлением результатов статистической обработки пробных опытов, проведенных при одних и тех же параметрах процесса, с расчетными значениями величин, вычисленных на основе математической модели. Классификация математических моделей в зависимости от использования управления процессом Математические модели делятся на: 1 Модели прогноза, или расчетные модели без управления Основное назначение этих моделей — дать прогноз о поведении системы во времени и в пространстве, зная начальное состояние и информацию о поведении ее на границе. Примерами могут служить модели распределения тепла, электрического поля, химической кинетики, гидродинамики. 2 Оптимизационные модели: стационарные модели используются на уровне проектирования различных технологических систем; динамические — как на уровне проектирования, так и, главным образом, для оптимального управления различными процессами — технологическими, экономическими и др. В задачах оптимизации имеется два направления. К первому относятся детерминированные задачи. Вся входная информация в них является полностью определяемой. Второе направление относится к стохастическим процессам. В этих задачах некоторые параметры носят случайный характер или содержат элемент неопределенности. Методы отыскания экстремума функции многих переменных с различными ограничениями часто называются методами математического программирования. Содержательная классификация моделей Была дана классификация математических моделей, используемых в физике и в естественных науках, а также эта классификация проанализирована и расширена. Она сфокусирована на этапе построения содержательной модели. 1 Гипотеза. Эти модели «представляют собой пробное описание явления, причем автор либо верит в его возможность, либо считает даже его истинным». Пример: модель Солнечной системы по Птолемею и модель Коперника (усовершенствованная Кеплером), модель атома Резерфорда и модель Большого Взрыва. Если модель первого типа построена, то это означает, что она временно признается за истину и можно сконцентрироваться на других проблемах. Однако это не может быть точкой в исследованиях, но только временной паузой: статус мо дели первого типа может быть только временным. 2 Феноменологическая модель. Данная модель содержит механизм для описания явления. Однако этот механизм недостаточно убедителен и не может быть подтвержден имеющимися данными или плохо согласуется с имеющимися теориями и накопленным знанием об объекте. Поэтому феноменологические модели имеют статус временных решений. Считается, что ответ все еще неизвестен, и необходимо продолжить поиск «истинных механизмов». Пример: модели теплорода и кварковая модель элементарных частиц. Роль модели в исследовании может меняться со временем, может случиться так, что новые данные и теории подтвердят феноменологические модели и те будут повышены до статуса гипотезы. Аналогично, новое знание может постепенно придти в противоречие с моделями-гипотезами первого типа и те могут быть переведены во второй. Так, кварковая модель постепенно переходит в разряд гипотез; атомизм в физике возник как временное решение, но с ходом истории перешел в первый тип. А вот модели эфира и сейчас находятся вне науки. 3 Приближение. Если можно построить уравнения, описывающие исследуемую систему, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый прием в этом случае — использование приближений. Уравнения заменяются линейными. Стандартный пример — закон Ома. 4 Упрощение. В данной модели отбрасываются детали, которые могут заметно и не всегда контролируемо повлиять на результат. Примеры: применение модели идеального газа к неидеальному, уравнение состояния Ван‑дер‑Ваальса, большинство моделей физики твердого тела, жидкостей и ядерной физики. Путь от микроописания к свойствам тел (или сред), состоящих из большого числа частиц, очень длинен. Приходится отбрасывать многие детали. 5 Эвристическая модель. Эвристическая модель сохраняет лишь качественное подобие реальности и дает предсказания только «по порядку величины». Типичный пример — приближение средней длины свободного пробега в кинетической теории. Оно дает простые формулы для коэффициентов вязкости, диффузии, теплопроводности, согласующиеся с реальностью по порядку величины. Но при построении новой физики далеко не сразу получается модель, дающая хотя бы качественное описание объекта. В этом случае часто используют модель по аналогии, отражающую действительность хоть в какой‑нибудь черте. 6 Аналогия. Данная модель впервые возникла, когда взаимодействие в системе нейтрон‑протон пытались объяснить посредством взаимодействия атома водорода с протоном. Эта аналогия и привела к заключению, что должны существовать обменные силы взаимодействия между нейтроном и протоном, которые аналогичны обменным силам в системе H — H+, обусловленным переходом электрона между двумя протонами. 7 Мысленный эксперимент. Сюда можно отнести рассуждения, которые в конечном итоге приводят к противоречию. 8 Демонстрация возможности. Это тоже мысленные эксперименты с воображаемыми сущностями, демонстрирующие, что предполагаемое явление согласуется с базовыми принципами и внутренне непротиворечиво. Один из самых знаменитых таких экспериментов — геометрия Лобачевского (Лобачевский называл ее «воображаемой геометрией»). Контрольные вопросы и задания 1 Что такое математическая модель и математическое моделирование? 2 Назовите элементы обобщенной математической модели. 3 Перечислите признаки, по которым классифицируются математические модели. 4 В чем отличие простых моделей от сложных? 5 Перечислите типы моделей в зависимости от применяемого оператора моделирования. 6 Как классифицируются модели в зависимости от входных и выходных параметров? 7 Чем отличаются дескриптивные и управленческие модели? 8 Для каких целей применяются прямые и обратные модели? 9 В чем отличие моделей прогноза от оптимизационных моделей? 10 Опишите типы содержательной классификации моделей. |
