Лабораторная работа № 1. Множества и операции над ними.
Порядок выполнения работы:
1) Рассмотреть решение приведенных заданий
2) По данному преподавателем варианту выполнить задания.
Примеры решения задач
Пусть  . Определить следующие множества:
Объединение множеств A, B – это множество, состоящее из всех элементов, которые принадлежат хотя бы одному из множеств A, B. Операция объединения обозначается как  .
Пересечение множеств A, B – это множество, содержащее все общие для A, B элементы. Операция пересечения обозначается как  .
Разность множеств A, B - это множество тех элементов A, которые не принадлежат B. Другими словами, из A удаляются общие для A и B элементы. Операция разности обозначается как A\B.
Симметрической разностью множеств A, B называется множество AB = (A\B)U(B\A).
Дополнение множества А есть множество, элементы которого принадлежат универсальному множеству U и не принадлежат А. Операция дополнения обозначается как  .
Решение.
Множество  есть пересечение двух множеств  и  ,
 .
Множество  есть дополнение пересечения двух множеств  и ,
 .
Множество  есть симметричная разность двух множеств и ,
Множество  есть пересечение двух множеств и  , что следует из порядка выполнения действий.  ,  .
Множество  есть объединение двух множеств  и , что следует из порядка выполнения действий.  ,  .
Множество  есть пересечение двух множеств  и  .
 ,  .  .
Множество  есть разность двух множеств и . 
Пусть  .
Найти . Убедиться, что  .
Решение: Найдем множество  .
 , тогда  .
Убедимся, что  . Левая часть равенства есть множество . Найдем правую часть. Множество  есть объединение двух множеств и  .  ,  , тогда  . Получилось верное равенство.
Пусть множество A состоит из точек М(х,у) плоскости, для которых  , множество В – из точек плоскости, для которых  , С – из точек плоскости для которых  >0. Требуется изобразить множество  .
Решение. Как следует из условия, множество А есть квадрат, В – круг, С – полуплоскость.
Решение приведено на рисунке
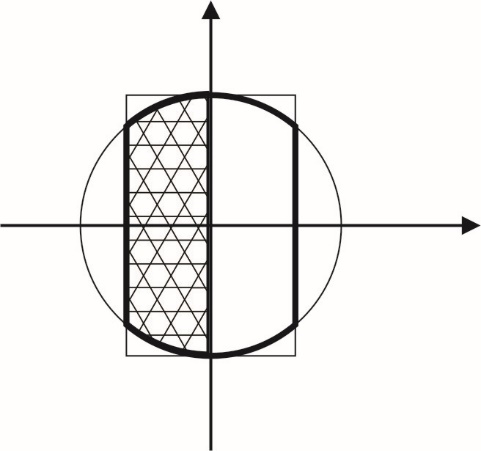
- «обрезанный прямоугольник», обведенный на рисунке жирной линией.
- множество точек, полученное удалением из точек полуплоскости >0. Окончательный результат выделен на рисунке штриховкой.
Среди 100 деталей прошли обработку на первом станке 42 штуки, на втором – 30 штук, а на третьем – 28. причем на первом и втором станках обработано 5 деталей, на первом и третьем – 10 деталей, на втором и третьем – 8 деталей, на всех трех станках обработано три детали. Сколько деталей обработано на первом станке и сколько деталей не обработано ни на одном из станков?
Решение. В качестве универсального выберем множество всех деталей. Число его элементов равно 100. Пусть А – множество деталей, обработанных на первом станке, В – на втором, С – на третьем. Число элементов множества А обозначим  . Оно равно 42, то есть  . Аналогично  . Обратимся к рисунку
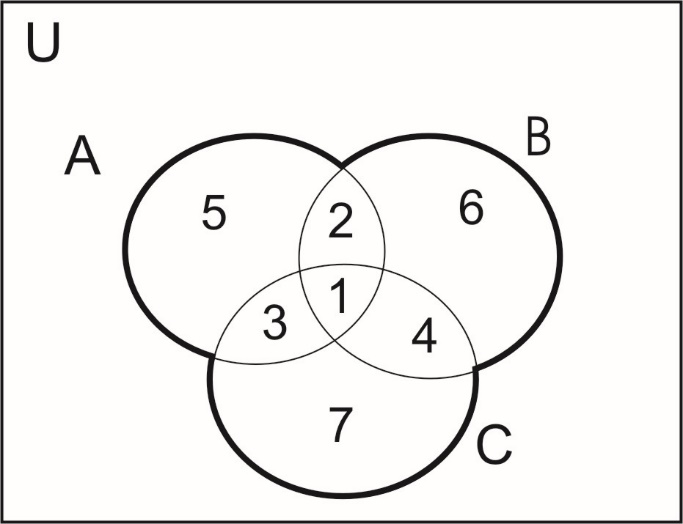
Обведенное на чертеже жирной линией множество  есть множество деталей, обработанных хотя бы на одном из станков. Оно разбито на 7 непересекающихся подмножеств, обозначенных на чертеже цифрами. Область 1 есть множество деталей, прошедших обработку на всех трех станках, то есть множество  . По условию задачи  . Множество деталей, обработанных на первом и втором станках, то есть множество есть сумма областей, помеченных цифрами 1 и 2. Причем область 2 – множество деталей, обработанных только на первом и втором станках.
По условию задачи  . Следовательно, число элементов деталей, обработанных только на первом и втором станках, равно 5-3=2. Аналогично, число элементов множества, обозначенного цифрой 3, есть число деталей, прошедших обработку на первом и третьем станках. Оно равно  . Число деталей, прошедших обработку только на втором и третьем станках (область 4), равно  .
Область, помеченная на чертеже цифрой 5, есть множество деталей, обработанных только на первом станке. Мы получим число элементов этого множества, если из числа всех обработанных на первом станке деталей вычесть число деталей, обработанных одновременно на первом и втором, на первом и третьем станках, а так же на всех трех станках, 42-(3+2+7)=30.
Аналогично, можно определить число деталей, обработанных только на втором станке (область 6), 30-(3+2+5)=20. Только на третьем (область 7) 28-(3+7+5)=13. Можно получить число всех обработанных деталей, то есть  , если сложить число элементов всех областей с 1 по 7. Оно равно 80. Дополнением к нему является множество необработанных деталей  ,  .
Лекции по экономике посещают 20 студентов, по математике – 30. Найти число студентов, посещающих лекции по экономике или математике, если 1) лекции проходят в одно и то же время, 2) лекции проходят в разные часы и 10 студентов слушают оба курса.
Решение. В первом случае имеем дело с непересекающимися множествами, так как студентов, посещающих оба курса, не существует, то есть  (пустое множество), тогда если А – множество студентов, посещающих лекции по математике, В – по экономике, то  а  .
Во втором случае, число студентов, посещающих лекции только по математике, - 10, так как из 20 человек 10 слушают оба курса. Аналогично только экономику слушают 20 человек из общего числа студентов, равного 30.
Следовательно, лекции по математике или экономике слушают 40 человек, так как  .
Доказать, что для произвольных множеств А и В имеет место соотношение  .
Доказательство: Доказательство правильности едет методом от противного. Допустим, что  . Рассмотрим левую часть:
 .
Рассмотрим правую часть  .
Тогда  , следовательно  Ø, нет такого элемента  . Пришли к противоречию, то есть  .
Аналогично доказывается, что  .
Решить систему уравнений.
Решение.
Из первого уравнения следует, что  . Из второго уравнения системы следует, что  , то есть  . Из первого уравнения следует, что  . Из второго уравнения системы следует, что  , значит  .
Доказать, что (А\В)\(В\С)=(А\В)\С
Задачи для самостоятельного решения.
1. Сформировать множества (размерность множеств минимум 7 элементов)
Вариант
|
|
1
|
Сформировать множества A, B, C.
Получить множество A∩(BUС),
доказать тождество А∩(ВUС)=(А∩В)U(А∩С).
Получить множество АU(В∩С),
доказать тождество АU(В∩С)=(АUВ)∩(А∩С).
|
2
|
Сформировать множества А, В, С.
Получить множество (АUВ)∩А,
доказать тождество (АUВ)∩А=А.
Получить множество А\(ВUС),
доказать тождество А\(ВUС)=(А\В)∩(А\С).
|
3
|
Сформировать множества А, В, С.
Получить множество А\(В∩С),
доказать тождество А\(В∩С)=(А\В)U(А\С).
Получить множество А\(A\B),
доказать тождество А\(A\B)=А∩В.
|
4
|
Сформировать множества А, В, С.
Получить множество А\(А∩В),
доказать тождество А\(А∩В)=А\В.
Получить множество А\(ВUС),
доказать тождество А∩(В\С)=(А∩В)\(А∩С).
|
5
|
Сформировать множества А, В, С.
Получить множество (А\В)\С,
доказать тождество (А\В)\С=(А\С)\(В\С).
Получить множество АU(B\A),
доказать тождество АU(B\A)=АUВ.
|
6
|
Сформировать множества А, В, C.
Получить множество (АUВ)\C,
доказать тождество (АUВ)\C=(А\C)U(В\C).
Получить множество А\(В\С),
доказать тождество А\(В\С)=(А\B)U(A∩С).
|
7
|
Сформировать множества А, В, С.
Получить множество А\(ВUС),
доказать тождество А\(ВUС)=(А\В)\С.
Получить симметрическую разность АВ,
доказать тождество АВ=ВА.
|
8
|
Сформировать множества А, В, С.
Получить множество (АUВ)\(A∩B),
доказать тождество (АUВ)\(A∩B)=АВ.
Получить множество А(ВС),
доказать тождество А(ВС)=(АВ)С.
|
9
|
Сформировать множества А, В, С.
Получить множество А∩(ВС),
доказать тождество А∩(ВС)=(А∩В)∆(А∩С).
Получить множество А(АВ),
доказать тождество А(АВ)=В.
|
10
|
Сформировать множества А, В.
Получить множество АВ(А∩В),
доказать тождество АВ(А∩В)=АUВ.
Получить множество А(А∩В),
доказать тождество А(А∩В)=А\В.
|
11
|
Сформировать множества А, В, С.
Получить множество (АВ)U(A∩В),
доказать тождество (АВ)U(A∩В)=АUВ.
Получить множество (А\C)U(В\C),
доказать тождество (А\C)U(В\C)=(АUВ)\C.
|
12
|
Сформировать множества А, В, С.
Получить множество (А\B)U(A∩С),
доказать тождество (А\B)U(A∩С)=А\(В\С).
Получить множество (А\В)\С,
доказать тождество (А\В)\С=А\(ВUС).
Получить множество (А\В)∩(А\С),
доказать тождество (А\В)∩(А\С)=А\(ВUС).
|
2. С помощью диаграмм Эйлера-Венна получить множество М. Варианты заданий в файле Задание 2.pdf
3.
Вариант
|
|
1
|
Каждый из 500 студентов посещают три спецкурса. Спецкурс только по математике, только по математике и физике, только по физике и астрономии посещают одинаковое число студентов; три спецкурса посещают 20 студентов. Спецкурс по математике посещают столько же студентов, сколько спецкурс по физике. Спецкурс только по физике посещают 50 студентов, а спецкурс по астрономии – 250 студентов. Сколько студентов посещают только один спецкурс?
|
2
|
Экзамен по математике содержал три задачи: по алгебре, по геометрии и по тригонометрии. Из 800 абитуриентов задачу по алгебре решили 250 человек, по алгебре или геометрии – 660 человек; по две задачи решили 400 человек, из них две задачи по алгебре и геометрии решили 150 человек, по алгебре и тригонометрии 50 человек. Только по тригонометрии задачи решили 120 человек. Ни один абитуриент не решил все задачи; 20 абитуриентов не решили ни одной задачи. Сколько абитуриентов решили задачи по геометрии? Сколько абитуриентов решили только одну задачу?
|
3
|
Среди 100 студентов института иностранными языками занимались: немецким – 30 человек, французским – 40 человека, испанским – 35, испанским и немецким – 8 человек, немецким и французским – 7 человек, испанским и французским – 9; 5 студентов изучали все три языка. Сколько студентов изучали только французский язык? Сколько студентов не изучали ни одного из иностранных языков?
|
4
|
Экзамен по математике содержал три задачи: по алгебре, по геометрии и по тригонометрии. Из 750 абитуриентов задачу по алгебре решили 400 абитуриентов, по геометрии – 480, по тригонометрии – 420; задачи по алгебре или геометрии решили 630 абитуриентов; по геометрии или тригонометрии – 600 абитуриентов; по алгебре или тригонометрии – 620 абитуриентов. 100 абитуриентов не решили ни одной задачи. Сколько абитуриентов решили все задачи? Сколько абитуриентов решили только одну задачу?
|
5
|
Каждый из 500 студентов обязан посещать хотя бы один из трех курсов: по математике, экономике, философии. Три курса посещают 10 студентов, по математике и экономике – 30, по математике и философии – 25, курс только по экономике – 80 студентов. Известно также, что курс по математике посещают 345 студентов, по экономике – 145, по философии – 100 студентов. Сколько студентов посещают курс только по философии? Сколько студентов посещают два курса?
|
6
|
На кафедре иностранных языков работают 37 преподавателей, из них французский преподают 23 преподавателя, английский язык 16 преподавателей, все три языка – три преподавателя. Число преподавателей, ведущих занятия только по английскому языку, равно числу преподавателей, ведущих занятия только по немецкому языку. Число преподавателей, ведущих занятия только по английскому и немецкому языкам, равно числу преподавателей, ведущих занятия только по немецкому и французскому языкам; 12 преподавателей проводят занятия только по двум иностранным языкам. Сколько преподавателей преподают один иностранный язык? Сколько преподавателей преподают один английский язык?
|
7
|
На курсы иностранных языков зачислено 300 слушателей. Из них французский или английский изучают 250 человек, английский и немецкий – 60 человек, английский и французский – 80 человек. Число слушателей, изучающих только французский язык, равно числу слушателей, изучающих только немецкий язык; 70 человек изучают только английский язык. Занятия по французскому и немецкому языкам проводятся одновременно. Сколько слушателей изучает немецкий или французский языки? Сколько слушателей не посещает занятия?
|
8
|
На курсах иностранных языков учатся 300 студентов, из них число студентов, изучающих английский или французский языки, равно 230 и равно числу студентов, изучающих французский или немецкий языки. Число студентов, изучающих английский или немецкий языки, равно 250, а число студентов, изучающих английский и французский языки равно 60. Студенты, изучающие английский язык, не изучают немецкого языка. Сколько студентов изучают каждый из указанных языков и сколько студентов изучают 2 языка одновременно?
|
9
|
Группа студентов из 25 человек сдала экзаменационную сессию со следующими результатами: 2 человека получили только «отлично»; 3 человека получили отличные, хорошие и удовлетворительные оценки; 4 человека только «хорошо»; 3 человека только хорошие и удовлетворительные оценки; число студентов, сдавших сессию только на «отлично» и «хорошо», равно числу студентов, сдавших сессию только на «удовлетворительно». Студентов, получивших только отличные и удовлетворительные оценки – нет. Удовлетворительные или хорошие оценки получили 22 студента. Сколько студентов не явилось на экзамены? Сколько студентов сдало сессию только на «удовлетворительно»?
|
10
|
На курсах иностранных языков учится 600 человек, из них французский изучают 220 человек, английский 270 человек, слушатели, изучающие английский язык, не изучают немецкий язык; один французский язык изучают 100 человек, один немецкий – 180 человек. Сколько человек изучают по два иностранных языка? Сколько человек изучают один иностранный язык?
|
4. Упростить выражение
 |
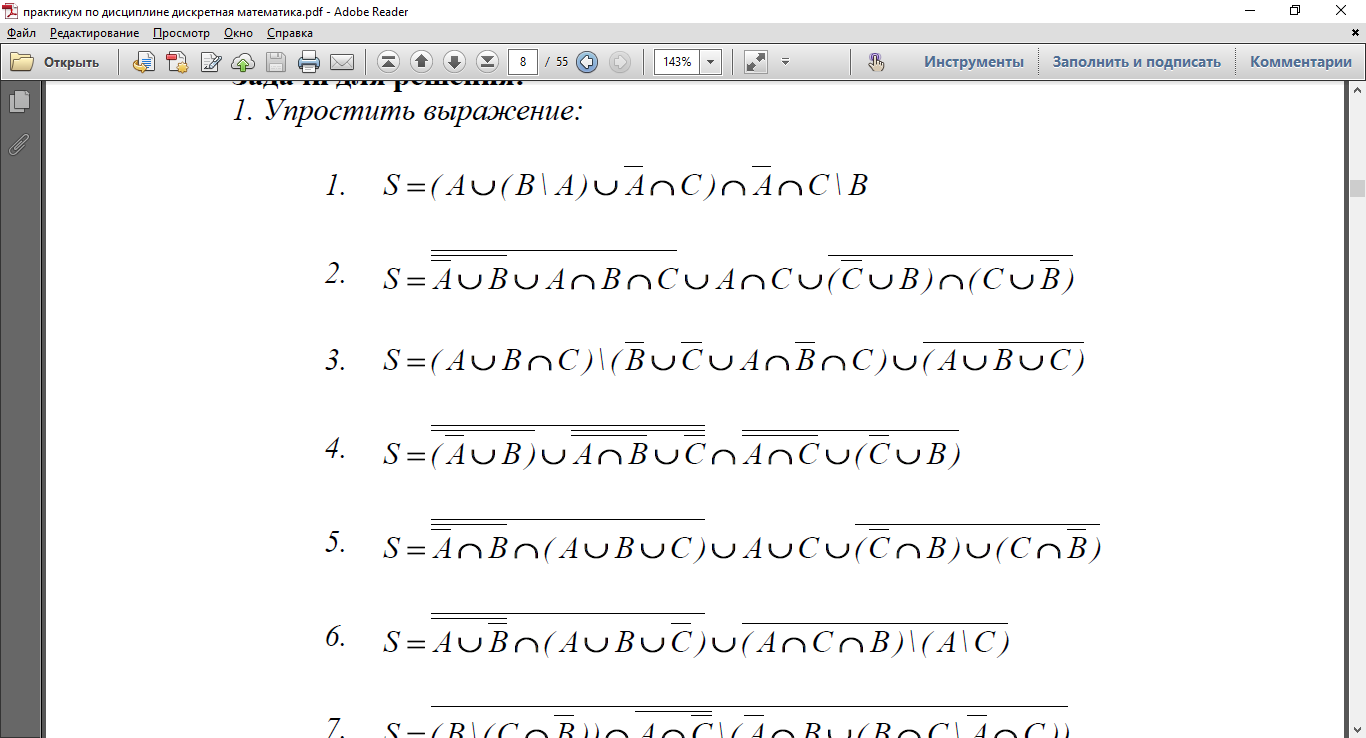
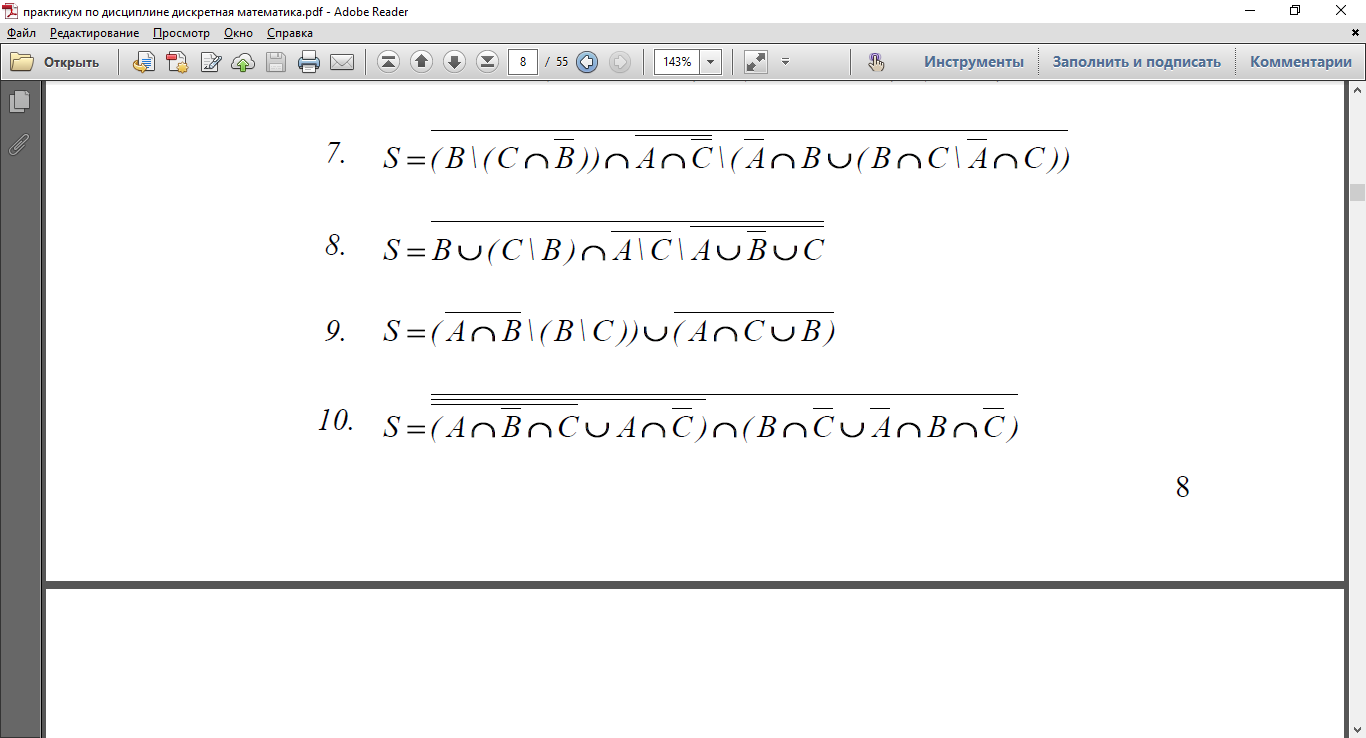Скачать 385.24 Kb.
