решение задач. Решение задач линейного программирования в MathCad. Лабораторная работа Решение задач линейного программирования в MathCad
 Скачать 215 Kb. Скачать 215 Kb.
|
|
Лабораторная работа № 3. Решение задач линейного программирования в MathCad. Задача 1. Задача линейного программирования. Найти максимальное значение функции при заданных ограничениях Решение. 1) Специальной переменной ORIGIN присваивают значение 1. Значением ORIGIN является номер первого элемента строки или столбца в матрице. По умолчанию ORIGIN=0. В меню Math выбрать строку Options или 2) Вводят исходные данные задачи в матричной форме. 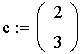 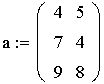 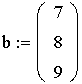 3) Вводят линейную целевую функцию. 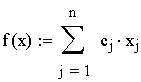 4) Задают начальные значения переменным задачи. 5) Вводят ограничения задачи в матричной форме. 6) Определяют оптимальное решение задачи с помощью встроенной функции Maximize (в случае поиска максимума функции) или Minimize (в случае поиска минимума функции). 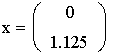 Задача 2. Транспортная задача. Имеются n пунктов производства и т пунктов распределения продукции. Стоимость перевозки единицы продукции с і-го пункта производства в j-й центр распределения cij приведена в таблице, где под строкой понимается пункт производства, а под столбцом - пункт распределения. Кроме того, в этой таблице в i-й строке указан объем производства в і-м пункте производства, а в j-м столбце указан спрос в j-м центре распределения. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.
Объем потребления Решение задачи средствами MathCAD: Введите исходные данные в матричной форме.  Введите линейную целевую функцию. 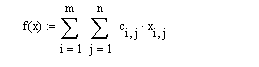 Задайте начальные значения переменных: Введите ограничения задачи в матричной форме. 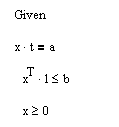 Определите оптимальное решение задачи с помощью встроенной функции Minimize: 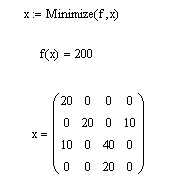 Задача 2. Задача о назначениях. Имеются n рабочих и т видов работ. Стоимость cijвыполнения і-и работником j-й работы приведена в таблице, где рабочему соответствует строка, а работе – столбец. Необходимо составить план работ так, чтобы все работы были выполнены, каждый рабочий был занят только на одной работе, а суммарная стоимость выполнения всех работ была минимальной.
Решение задачи средствами MathCAD: Введем исходные данные в матричной форме. 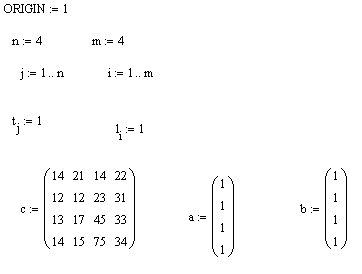 Вводим линейную целевую функцию. 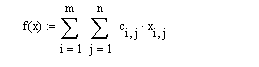 Зададим начальные значения переменных: Вводим ограничения задачи в матричной форме. 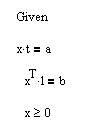 Определяем оптимальное решение задачи с помощью встроенной функции Minimize: 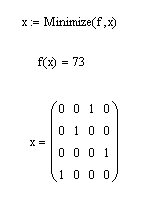 Задачи для самостоятельного решения: Задание 1.Задача об использовании ресурсов. Для изготовления двух видов продукции П1 и П2 используются четыре вида ресурсов Р1, Р2, Р3, Р4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1. Таблица 1. Числовые данные для задания 1
Прибыль, получаемая от единицы продукции П1, П2 соответственно равна 2 и 3 ден. ед. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Примечание:k—номер варианта. Задание 2. Задача планирования производства. Вариант 1. Для изготовления двух видов продукции P1 и P2 используют четыре вида ресурсов S1, S2, S3 и S4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, прибыль, получаемая от единицы продукции, приведены в таблице:
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Вариант 2. Для производства двух видов изделий А и В предприятие использует три вида сырья. Другие условия задачи приведены в таблице.
Составить такой план выпуска продукции, при котором прибыль предприятия от реализации продукции будет максимальной при условии, что изделий В надо выпустить не менее чем изделий А. Вариант 3. Для изготовления трех видов изделий А,В и С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования, общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия каждого вида указаны в таблице:
Требуется определить, сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была бы максимальной. Вариант 4. Кондитерская фабрика для производства трех видов карамели А, В и С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство 1 т карамели данного вида, общее количество сырья каждого вида, которое может быть использовано фабрикой, а также прибыль от реализации 1 т карамели данного вида приведены в таблице:
Найти план производства карамели, обеспечивающий максимальную прибыль от ее реализации. Вариант 5. Для изготовления различных изделий А, В и С предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в таблице:
Изделия А, В и С могут производиться в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида. Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной. Вариант 6. Для изготовления двух видов продукции P1 и P2 используют три вида ресурсов S1, S2, S3. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, прибыль, получаемая от единицы продукции, приведены в таблице:
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Вариант 7. Для изготовления двух видов продукции P1 и P2 используют четыре вида ресурсов S1, S2, S3. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, прибыль, получаемая от единицы продукции, приведены в таблице:
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Вариант 8. Для изготовления двух видов продукции P1 и P2 используют четыре вида ресурсов S1, S2, S3. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, прибыль, получаемая от единицы продукции, приведены в таблице:
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Вариант 9. Для изготовления двух видов продукции P1, P2, P3 и P4 используют четыре вида ресурсов S1, S2, S3. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, прибыль, получаемая от единицы продукции, приведены в таблице:
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Вариант 10. Для изготовления двух видов продукции P1 – P4 используют четыре вида ресурсов S1, S2, S3. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, прибыль, получаемая от единицы продукции, приведены в таблице:
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Задание 3. Транспортная задача Задание 1. Туристической фирме необходимо разместить три группы туристов Т1, Т2, Т3 количеством 60 + k, 120 + k и 100 + k человек соответственно, прибывших в аэропорты, по четырем гостиницам Г1, Г2, Г3, Г4. Стоимость перевозки одного туриста и количество свободных номеров в гостиницах указаны в таблице 4.2. Таблица 4.2. Числовые данные для задания 2
Составить план перевозок туристов из аэропортов в гостиницы, который обеспечит минимальные транспортные издержки при условиях размещения всех туристов и заполнения всех свободных мест в гостиницах. Примечание:k—номер варианта. Задание 4. Транспортная задача Вариант 1. Для строительства четырех объектов используется кирпич, изготовляемый на трех заводах. Ежедневно каждый из заводов может изготовлять 100, 150 и 50 усл. ед. кирпича. Ежедневные потребности в кирпиче на каждом из строящихся объектов соответственно равны 75, 80, 60 и 85 усл. ед. Известны также тарифы перевозок 1 усл. ед. кирпича с каждого с заводов к каждому из строящихся объектов: 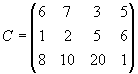 Составить такой план перевозок кирпича к строящимся объектам, при котором общая стоимость перевозок является минимальной. Вариант 2. На трех хлебокомбинатах ежедневно производится 110, 190 и 90 т муки. Эта мука потребляется четырьмя хлебозаводами, ежедневные потребности которых равны соответственно 80, 60, 170 и 80 т. Тарифы перевозок 1 т муки с хлебокомбинатов к каждому из хлебозаводов задаются матрицей 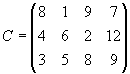 Составить такой план доставки муки, при котором общая стоимость перевозок является минимальной. Вариант 3. В трех хранилищах горючего ежедневно хранится 175, 125 и 140 т бензина. Этот бензин ежедневно получают четыре заправочные станции в количествах, равных соответственно 180, 160, 60 и 40 т. Стоимости перевозок 1 т бензина с хранилищ к заправочным станциям задаются матрицей 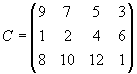 Составить такой план перевозок бензина, при котором общая стоимость перевозок является минимальной. Вариант 4. На трех железнодорожных станциях А1, А2 и А3 скопилось 120, 110 и 130 незагруженных вагонов. Эти вагоны необходимо перегнать на железнодорожные станции В1, В2, В3, В4 и В5. На каждой из этих станций потребность в вагонах соответственно равна 80, 60, 70, 100 и 50. Тарифы перегонки одного вагона определяются матрицей 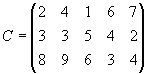 Составьте такой план перегонок вагонов, чтобы общая стоимость была минимальной. Вариант 5. Для строительства трех дорог используется гравий из четырех карьеров. Запасы гравия в каждом из карьеров соответственно равны 120, 280 и 160 усл. ед. Потребности в гравии для строительства каждой из дорог соответственно равны 130, 220, 160 и 50 усл. ед. Известны также тарифы перевозок 1 усл. ед. гравия из каждого из карьеров к каждой из строящихся дорог, которые задаются матрицей 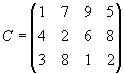 Составить такой план перевозок гравия, при котором потребности в нем каждой из строящихся дорог были бы удовлетворены при наименьшей общей стоимости перевозок. Вариант 6. Три предприятия данного экономического района могут производить некоторую однородную продукцию в количествах, соответственно равных 180, 350 и 20 ед. Эта продукция должна быть поставлена пяти потребителям в количествах, соответственно равных 110, 90, 120, 80 и 150 ед. Затраты, связанные с производством и доставкой единицы продукции, задаются матрицей 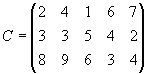 Составить такой план прикрепления получателей продукции ее поставщикам, при котором общая стоимость перевозок является минимальной. Вариант 7. Производственное объединение имеет в своем составе три филиала, которые производят однородную продукцию соответственно в количествах, равных 50, 30 и 10 ед. Эту продукцию получают четыре потребителя, расположенные в разных местах. Их потребности соответственно равны 30, 30, 10 и 20 ед. Тарифы перевозок единицы продукции от каждого из филиалов соответствующим потребителям задаются матрицей 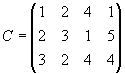 Составить такой план прикрепления получателей продукции ее поставщикам, при котором общая стоимость перевозок является минимальной. Вариант 8.На трех складах оптовой базы сосредоточен однородный груз в количествах 180, 60 и 60 ед. Этот груз необходимо перевезти в четыре магазина. Каждый из магазинов должен получить соответственно 120, 40, 60 и 80 ед. груза. Тарифы перевозок единицы груза из каждого из складов во все магазины задаются матрицей 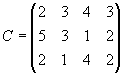 Составить такой план перевозок, при котором общая стоимость перевозок является минимальной. Вариант 9. Четыре предприятия данного экономического района для производства продукции используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 120,50,190 и 110 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 160, 140, 170 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей. 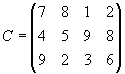 Составить такой план перевозок, при котором общая стоимость перевозок является минимальной. Вариант 10. Четыре предприятия данного экономического района для производства продукции используют пять видов сырья. Потребности в сырье каждого из предприятий соответственно равны 120,50,190 и 110 ед. Сырье сосредоточено в пяти местах его получения, а запасы соответственно равны 160, 100, 40, 100 и 70 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей. 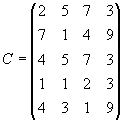 Составить такой план перевозок, при котором общая стоимость перевозок является минимальной. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
