математика. Заказ 4642622 (Восстановлен). Задание Оптимальное планирование
 Скачать 212.8 Kb. Скачать 212.8 Kb.
|
|
Задание № 6. Оптимальное планирование. Постановка задачи: предприятие располагает ресурсами сырья, рабочей силы и оборудованием, необходимыми для производства любого из трех видов производимых товаров 1, 2, 3. Затраты ресурсов на изготовление единицы данного вида товаров; прибыль, получаемая от реализации единицы товара, а также запасы ресурсов указаны в следующей таблице: Таблица №1
Определить, какой ассортимент товара надо выпускать, чтобы прибыль была максимальной. Исходную информацию можно представить в виде векторов и матрицы: А = (аij) = 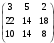 - матрица затрат ресурсов на единицу продукции. В = - матрица затрат ресурсов на единицу продукции. В = 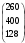 - вектор запаса ресурсов сырья, рабочей силы и оборудования. Р = - вектор запаса ресурсов сырья, рабочей силы и оборудования. Р = 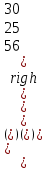 - вектор прибыли от единицы товара 1, 2, 3. - вектор прибыли от единицы товара 1, 2, 3. Информацию записать в виде таблицы № 1. построить модель. Решить симплексным методом. Проанализировать полученный результат. Решение. Таблица № 1
По условию задачи для производства единицы товара 1 вида требуется затратить 3 кг сырья, 22 ч. рабочей силы и 10 станко-час. ресурсов оборудования. Для производства единицы товара 2 вида требуется затратить 5 кг сырья, 14 ч. рабочей силы и 14 станко-час. ресурсов оборудования. Для производства единицы товара 3 вида требуется затратить 2 кг сырья, 18 ч. рабочей силы и 8 станко-час. ресурсов оборудования. Производство обеспечено запасами сырья в количестве 260 кг, ресурсами рабочей силы в количестве 400 ч., ресурсами оборудования в количестве 128 станко-час. Прибыль от реализации единицы готового товара 1 вида составит 30 руб., товара 2 вида – 25 руб., товара 3 вида – 56 руб. Необходимо найти оптимальный план производства товаров 1, 2 и 3 видов 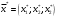 , обеспечивающий максимальную прибыль от их реализации при условии, что потребление ресурсов по каждому виду товаров не превзойдет имеющихся запасов. , обеспечивающий максимальную прибыль от их реализации при условии, что потребление ресурсов по каждому виду товаров не превзойдет имеющихся запасов.Обозначим через x1 – количество товара 1 вида, x2 – количество товара 2 вида, x2 – количество товара 3 вида, планируемое к производству. В условии задачи сформулированы ограничения на запасы каждого вида ресурса, т.е. потребление ресурсов по каждому виду не превзойдет имеющихся запасов bi. Кроме того, необходимо указать неотрицательность переменных x1≥0, x2≥0, x3≥0. Запишем эти ограничения в виде системы неравенств (составляем математическую модель): 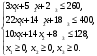 (1) (1)Составим целевую функцию общей прибыли, получаемой от реализации всех произведённых единиц товаров. Таким образом, получаем задачу линейного программирования: 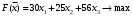 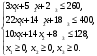 Решим полученную задачу линейного программирования симплекс-методом. Задача остается прежней. Приведем стандартную форму системы неравенств (1) в каноническую форму системы уравнений путем введения дополнительных балансовых переменных x4, x5,x6 со знаком «+», если знак неравенства «», и со знаком «–», ели знак неравенства «»: 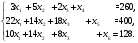 Переменные х4, х5, х6 будут базисными. Решим систему уравнений относительно базисных переменных: 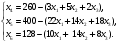 Функцию цели запишем в виде: 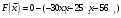 . .Полагая, что свободные переменные х1=0, х2=0, х3=0, получим первый опорный план 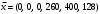 , , 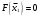 , в котором базисные переменные х4 = 260, х5 = 400, х6 = 128, следовательно товары не продаются и прибыль равна нулю, а ресурсы не используются. Запишем первый опорный план в симплексную таблицу: , в котором базисные переменные х4 = 260, х5 = 400, х6 = 128, следовательно товары не продаются и прибыль равна нулю, а ресурсы не используются. Запишем первый опорный план в симплексную таблицу:Таблица №2
Первый опорный план не оптимальный, так как в индексной строке находятся отрицательные коэффициенты: 30, 25, 56. За ведущий столбец выберем столбец, соответствующий переменной х3, так как сравниваемая по модулю имеем: |56| > {|30|, |25|}. Рассчитываем значения 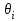 по строкам, как частное от деления по строкам, как частное от деления 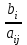 и выбираем наименьшее: и выбираем наименьшее: 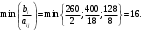 Следовательно, вторая строка является ведущей. Элемент 8 находится на пересечении ведущего столбца и ведущей строки (выделяем). Формируем следующую симплексную таблицу. Вместо переменной х6 в план II войдет переменная х3. Строка, соответствующая переменной х3 в плане II, получена в результате деления всех элементов строки х5 плана I на разрешающий элемент РЭ = 8. на месте разрешающего элемента в плане II получаем 1, в остальных клетках столбца х3 плана II записываем нули. Таким образом в новом плане II заполнены строки х3 и столбец х3. Все остальные элементы нового плана II, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ = 8. Во второй вершине по диагонали находится старое значение элемента, например, значение целевой функции 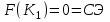 , которое указывает на место расположения нового НЭ в новом плане II. Третий элемент А = 128 и четвертый элемент В = 56 завершают построение прямоугольника в недостающих двух вершинах и расположены по другой диагонали. Значение нового элемента в плане II находится из выражения: , которое указывает на место расположения нового НЭ в новом плане II. Третий элемент А = 128 и четвертый элемент В = 56 завершают построение прямоугольника в недостающих двух вершинах и расположены по другой диагонали. Значение нового элемента в плане II находится из выражения: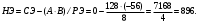 Элементы первой строки определяются аналогично: 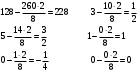 Все элементы, расположенные на пересечении строк и столбцов, соответствующих одноименным базисным элементам равны 1, остальные элементы столбца в базисах векторов, включая индексную строку, равны 0. Аналогично проводятся расчеты по всем строкам таблицы, включая индексную. Выполняя последовательно все этапы алгоритма, формируем план II: 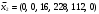 , , 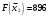 . Так как все коэффициенты в индексной строке неотрицательны, то полученный план оптимален. Согласно этому плану необходимо производить 16 единиц товара третьего вида, производство остальной продукции является нерентабельным. Максимальная прибыль при этом будет равна 896 руб. . Так как все коэффициенты в индексной строке неотрицательны, то полученный план оптимален. Согласно этому плану необходимо производить 16 единиц товара третьего вида, производство остальной продукции является нерентабельным. Максимальная прибыль при этом будет равна 896 руб. Ответ: максимальная прибыль 896 руб. будет получена, если производить 16 ед. товара 3 вида. Задание №7. Графический метод. Постановка задачи: для изготовления двух видов продукции имеются три вида ресурсов, объемы которых ограничены величинами b1,b2,b3 соответственно. Расход i-го вида ресурса на изготовление одной единицы j-го вида продукции равен aij, i=1, 2, 3,j=1, 2. Объем выпуска каждого из видов продукции ограничен числом x*1 и x*2 единиц, а прибыль, получаемая от реализации одной единицы изготовленной продукции равна c1 и c2 соответственно. Данные задачи могут быть представлены в форме таблицы:
Требуется составить план выпуска продукции (число единиц продукции по каждому виду), удовлетворяющий принятым ограничениям и приносящий максимум прибыли после реализации выпущенной продукции, имея следующие данные. A=  , b = , b = 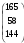 , x* = ( , x* = (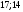 ), c = (7;2). ), c = (7;2).Решение. Запишем исходную информацию в виде таблицы: Таблица №3
Из таблицы следует, что для производства единицы продукции 1 вида требуется затратить 3 ед. ресурса 1, 2 ед. ресурса 2 и 8 ед. ресурса 3. Для производства единицы продукции 2 вида требуется затратить 114 ед. ресурса 1, 3 ед. ресурса 2 и 1 ед. ресурса 3. Производство обеспечено запасами 1 ресурса в количестве 165 ед., 2 ресурса – 58 ед., 3 ресурса – 144 ед. Прибыль от реализации единицы продукции 1 вида составит 7 у. е., продукции 2 вида – 2 у. е. Заранее планируется произвести продукции 1 вида в количестве не более 17 ед., продукции 2 вида – не более 14 ед. Необходимо найти оптимальный план производства продукции 1 и 2 видов 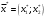 , обеспечивающий максимальную прибыль от ее реализации при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов. , обеспечивающий максимальную прибыль от ее реализации при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов.Обозначим через x1 – количество продукции 1 вида, x2 – количество продукции 2 вида, планируемое к производству. В условии задачи сформулированы ограничения на запасы каждого вида сырья, т.е. потребление ресурсов по каждому виду (1, 2, 3) не превзойдет имеющихся запасов bi. Кроме того, ограничения накладываются на общее количество производимой продукции (не более 17 и 14 ед.), а также необходимо указать неотрицательность переменных x1≥0, x2≥0. Запишем эти ограничения в виде системы неравенств (составляем математическую модель): 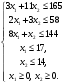 (2) (2)Составим целевую функцию общей прибыли, получаемой от реализации всей произведенной продукции. Таким образом, получаем задачу линейного программирования: 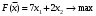 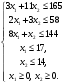 В системе ограничений (2) знаки неравенств заменим на знаки точных равенств и по полученным уравнениям строятся прямые на плоскости x1Ox2. В нашем случае система уравнений будет иметь вид: 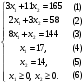 Построим по полученным уравнениям прямые и пронумеруем их (см. рис.1). - прямая (1) проходит через точки (0,15) и (22,9), - прямая (2) проходит через точки (0, 58/3) и (29,0), - прямая (3) проходит через точки (15,24) и (18,0), - прямая (4) проходит через точку (17,0) параллельно оси ординат, - прямая (5) проходит через точку (0,14) параллельно оси абсцисс, - прямая (6) совпадает с осью ординат, - прямая (7) совпадает с осью абсцисс. Чтобы определить полуплоскость, задаваемую каждым из неравенств, подставим в каждое неравенство координаты (0,0) начала системы координат. Полуплоскости, соответствующие неравенствам, обозначим стрелкой. Областью ОДР будет выпуклый многоугольникOАBCDE, который получается в результате пересечения полуплоскостей. Стороны этого многоугольника являются прямыми уравнений системы ограничений. Каждая вершина этого многоугольника является опорным планом. Из точки (0; 0) строим вектор 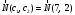 . Начальная линия уровня будет иметь вид: . Начальная линия уровня будет иметь вид: 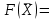 7x1 + 2x2 = 0 (на рисунке линии уровня обозначим прерывистой линией). 7x1 + 2x2 = 0 (на рисунке линии уровня обозначим прерывистой линией). 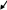 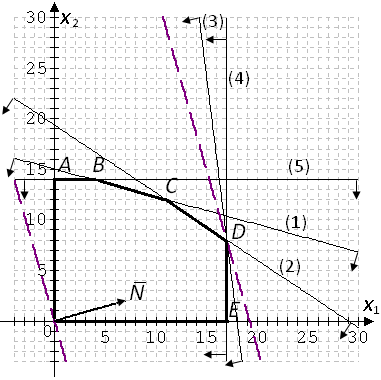 Рис. 1. Перемещая линию уровня вдоль вектора 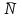 до тех пор, пока она не будет иметь с многоугольником ОДР не более одной точки пересечения, получим, что функция Fпринимаетmax значение в точке D – самой крайней сверху вершине многоугольника ОДР (см. рис.2). Точка D является точкой пересечения прямых (2) и (3). до тех пор, пока она не будет иметь с многоугольником ОДР не более одной точки пересечения, получим, что функция Fпринимаетmax значение в точке D – самой крайней сверху вершине многоугольника ОДР (см. рис.2). Точка D является точкой пересечения прямых (2) и (3).Находим координаты точки D, решая систему уравнений этих прямых (2) и (3): 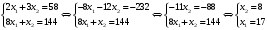 . .Решением системы будут значения x1 = 17, x2 = 8, т.е. B(17; 8). Тогда 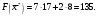 Таким образом, решением задачи является оптимальный план 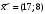 , дающий max значение функции , дающий max значение функции 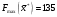 . . Ответ: максимальная прибыль 139 у.е. будет получена, если производить 4 ед. продукции 1 вида и 15 ед. продукции 2 вида. Задание № 8. Транспортная задача. Постановка задачи: на складах А1, А2, А3 имеются запасы продукции в количествах 180, 300, 120. Потребители В1, В2, В3 должны получить эту продукцию в количествах 110, 350, 140. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т. продукции заданы матрицей С (ден. ед.). С =  Решение. Составим математическую модель задачи. Обозначим xij количество товара, планируемого к доставке с i-го склада в j-й магазин. Так как cij стоимость перевозки единицы товара с i-го склада в j-й магазин, то перевозки с i-го склада в j-й магазин обойдутся в cijxij у. е., а в сумме перевозки обойдутся в 5x11 + 2x12 +2 x13+ x21 + 4x22 + 5x23 + 6x31 + 3x32 + 8x33 у. е. Таким образом, 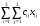 целевая функция, которую необходимо минимизировать (суммарная стоимость перевозок должна быть должна быть минимальной): целевая функция, которую необходимо минимизировать (суммарная стоимость перевозок должна быть должна быть минимальной): 5x11 + 2x12 +2 x13+ x21 + 4x22 + 5x23 + 6x31 + 3x32 + 8x33 min. По условию 1-й склад отправляет потребителям x11 + x12 + x13 т. продукции, и он должен использовать все свои запасы: x11 + x12 + x13 = 180. И, вообще, рассуждая относительно i-го склада, получаем уравнение xi1+xi2+xi3 +xi4 +xi5 = ai (i=1, 2, 3). Также по j-му потребителю (j=1, 2, 3), получаем уравнения x1j+ x2j+x3j = bj (j=1, 2, 3). Кроме того, по смыслу задачи количество xij перевозимого груза не может быть отрицательным: xij 0. Таким образом, математическая модель данной задачи: 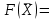 5x11 + 2x12 +2 x13+ x21 + 4x22 + 5x23 + 6x31 + 3x32 + 8x33 min. 5x11 + 2x12 +2 x13+ x21 + 4x22 + 5x23 + 6x31 + 3x32 + 8x33 min.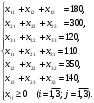 Найдём суммарный запас 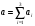 и суммарную потребность и суммарную потребность 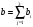 в грузе: в грузе: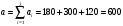 ; ; 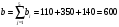 . .Получаем, что суммарный запас груза на базах равен суммарной потребности в магазинов в товаре. Следовательно, модель данной транспортной задачи является закрытой. Строим распределительную таблицу Таблица №4
Начинаем ее заполнять с клетки (2; 1), имеющей минимальную стоимость с21 = 1: х21 = min(а2; b1) = min(300; 110) = 110. Из дальнейшего рассмотрения исключаем 1-й столбец, отметив его номером (1). Затем заполняем клетку (1; 2), имеющую минимальную стоимость из оставшихся с12 = 2: x12 = min(а1; b2) = min(180; 350) = 180. Из дальнейшего рассмотрения исключаем 1-ю строку, отметив её номером (2). Аналогично заполняем остальные клетки. Получаем опорный план: Таблица №5
Со стоимостью перевозок: 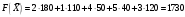 у. е. у. е.Ранг матрицы системы 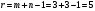 и число заполненных клеток 5 (= r). Следовательно, полученный план – невырожденный. Проверим опорный план на оптимальность методом потенциалов. и число заполненных клеток 5 (= r). Следовательно, полученный план – невырожденный. Проверим опорный план на оптимальность методом потенциалов.Найдем потенциалы 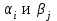 по занятым клеткам таблицы, решая систему уравнений, полагая что по занятым клеткам таблицы, решая систему уравнений, полагая что 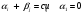 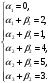 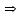 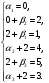 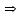 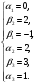 Занесем рассчитанные потенциалы в таблицу. Таблица №6
Подсчитаем оценки свободных клеток, полагая, что для них 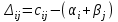 : :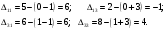 Первый опорный план является неоптимальным, так как 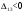 , поэтому переходим к его улучшению. Выбираем максимальную по модулю оценку свободной клетки , поэтому переходим к его улучшению. Выбираем максимальную по модулю оценку свободной клетки 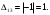 Для клетки (1,3) построим цикл перераспределения груза. Для этого в перспективную клетку (1,3) поставим знак +, а в остальных вершинах многоугольника чередующиеся знаки , +, : Таблица №7
Затем из чисел 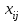 , стоящих в минусовых клетках, выбираем наименьшее, т.е. , стоящих в минусовых клетках, выбираем наименьшее, т.е. 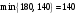 . Прибавляем 140 к объемам грузов, стоящих в плюсовых клетках и вычитаем 140 из . Прибавляем 140 к объемам грузов, стоящих в плюсовых клетках и вычитаем 140 из 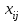 , стоящих в минусовых клетках. В результате получим новый опорный план II. , стоящих в минусовых клетках. В результате получим новый опорный план II.Таблица №8
Методом потенциалов определяем оценки клеток: Таблица №9
Поскольку все оценки неотрицательны, то план оптимален: 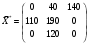 Его стоимость равна 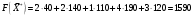 у. е. у. е.Ответ: чтобы затраты на перевозку были минимальными и составили 1590 у.е., необходимо поставить первому потребителю 110 т. продукции со 2-го склада; второму потребителю 40 т. продукции с 1-го склада, 190 т. продукции со 2-го склада и 120 т. продукции с 3-го склада; третьему потребителю 110 т. продукции с 1-го склада. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 18
18
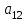
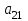
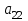
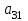
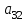
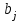
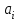
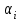
 2
2