Лабораторная работа Выполнил студент 1 курса Базуев Дмитрий Олегович по специальности направлению
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Министерство науки и высшего образования Российской Федерации ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ Филиал пермского национально исследовательского политехнического университета. (ЧФ ПНИПУ) Лабораторная работа № 0. Выполнил студент 1 курса Базуев Дмитрий Олегович. по специальности / направлению 13.03.02 «Электроэнергетика и электротехника.» Принял Доктор технических наук, профессор Морозов Евгений Александрович Доклад принят «__»____2022 г. Оценка: ____________________________ Чайковский, 2022 Программа для создания функции графиков. Актуальность: Актуальность данной работы обусловлена необходимостью компьютерного обеспечения при исследовании самых различных областях знаний. Преимущество: Программа разработана на языке программирования Pascal на одном из самых популярных языков. Она доступна в использовании. Вследствие простаты она занимает не значительное место в памяти компьютера и может быть размещена на flash-накопителе . Возможности: Программа позволяет осуществлять следующие действия : менять масштаб, менять центр начала координат, изменять цвет графиков, строить несколько графиков , предусмотрено наличие сетки, решать деференцированные и алгебраические уравнения, программа может моделировать процессы физические и технические процессы . Пример графиков функций которые она может построить: Y:=Power (X,n) - возведение X в степень n} {Y:=Ln(X) - натуральный логарифм от X) {Y:=Exp(X) - экспонента X} {Y:=Abs(X) - модуль X} {Y:=Sqr(X) - квадрат X} {Y:=Sqrt(X) - квадратный корень из X} {Y:=Sin(X) - синус X} {Y:=Cos(X) - косинус X} {Z:=Exp(Y*Ln(X) - X в степени Y} {X:=Pi - числор Пи} {f:=f*(pi/180) - гпадусы нужно переводить в радианы} Применение: Программу можно и использовать в учебных заведениях. Для поведения научных работ и компьютерных экспериментов . Графики.  Рис 1. Самый простой частный случай линейной зависимости - прямая пропорциональность у = kx, где k ≠ 0 - коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. 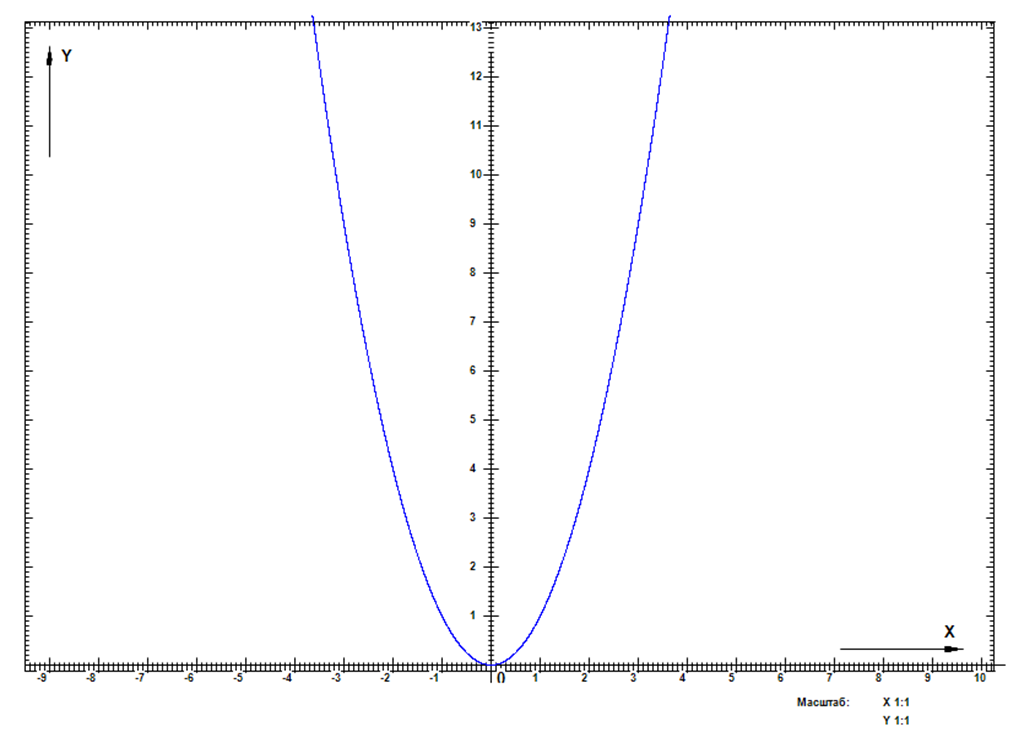 Рис 2 Простейший случай квадратичной зависимости - симметричная парабола с вершиной в начале координат.  Рис 3. Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Движение графиков функций». 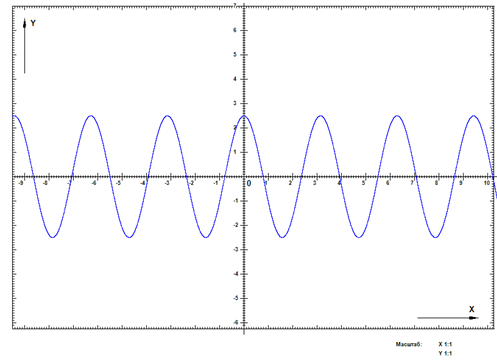 Рис 4 Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Движение графиков функций». 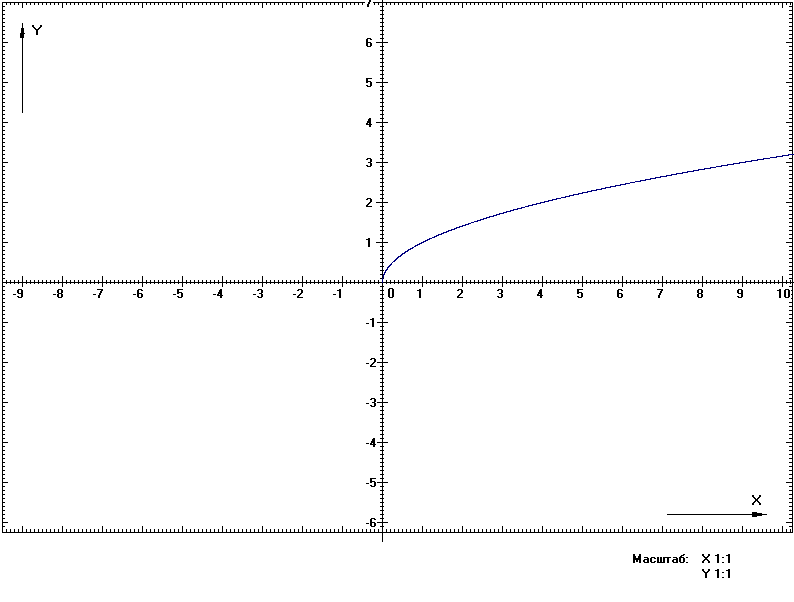 Рис 5 Самый простой случай для дробной степени (x1/2=√x). Случаи с коэффициентами изучаются в разделе «Движение графиков» функций". 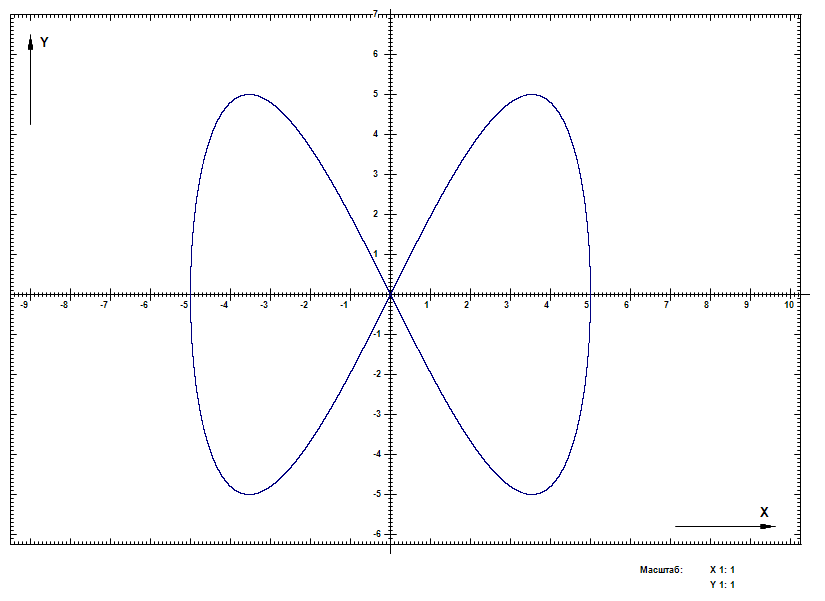 Рис 6 На графике 6 приведён результат работы программы. График представлен функцией фигура Лиссажу. Фигуры Лиссажу — траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Вывод: Паскаль очень удобен, поскольку применяется для работы с различными видами задач (вычислительных, обработки текстов, построения графических изображений, поиска информации и т.д).  Рис 7  Рис8  Рис 9   |
