хуй. МУ Лабораторная работа 1-4. Лабораторная работа 14 изучение колебаний физического маятника

• Название: Лабораторная работа 14 изучение колебаний физического маятника
• Дата: 02.09.2022
• Размер: 187.5 Kb.
• Имя файла: МУ Лабораторная работа 1-4.doc
• Тип: Лабораторная работа; #659124

Лабораторная работа № 1-4

ИЗУЧЕНИЕ КОЛЕБАНИЙ ФИЗИЧЕСКОГО МАЯТНИКА

ЦЕЛЬ РАБОТЫ: измерение периода колебаний, логарифмического декремента затухания и добротности физического маятника.

Введение

Колебания - периодические движения механической системы, которые она совершает вблизи своего положения устойчивого равновесия. Устойчивому равновесию соответствует минимум потенциальной энергии системы, отклонение от этого положения приводит к возникновению силы, которая стремится возвратить систему к положению равновесия.

При гармонических колебаниях смещение x зависит от времени по закону синуса или косинуса
. (1)
В этом выражении A - амплитуда колебания, т.е. максимальное отклонение от положения равновесия, аргумент синуса называется фазой колебания;  - начальная фаза,  - циклическая частота колебаний. Время, в течение которого совершается одно колебание (Т₀) называется периодом, а число колебаний за 1 секунду – частотой (₀).

Все указанные величины взаимосвязаны
. (2)
Гармонические колебания возникают, если возвращающаяся сила пропорциональна смещению х
.
Второй закон Ньютона применительно к этому случаю, записывается в следующем виде:
. (3)
Здесь - вторая производная по времени от смещения, а m и k- материальные характеристики механической системы. Циклическая частота колебаний определяется их значениями
; . (4)
При гармонических колебаниях выполняется закон сохранения механической энергии.

Выражение для кинетической энергии:

и потенциальной энергии:
,
то полная механическая энергия системы
. (5)
Экспериментальное определение периода колебаний, состоит в определении времени t, за которое совершается N колебаний. Период расчитывается по формуле
. (6)
Колебания, амплитуда которых убывает со временем, называются затухающими. Уменьшение амплитуды обусловлено уменьшением (дессипацией) энергии колебаний за счет работы сил трения. В случае малых отклонений от положения равновесия трение пропорционально скорости
.
Уравнение движения для системы содержит в этом случае силу упругости и силу трения:
, (7)
где  - коэффициент трения.

Зависимость смещения от времени получается убывающей
, (8)

где - называют коэффициентом затухания. Решение (8) справедливо при . Циклическая частота затухающих колебаний определяется формулой
. (9)
Поскольку амплитуда затухающих колебаний уменьшается со временем по закону
, (10)
то энергия колебаний тоже будет убывать
. (11)
При затухающие колебания становятся не периодическими, а трение, при котором это возникает называется критическим. Для характеристики затухающих колебаний используются логарифмический декремент затухания D и добротность Q.

Декремент затухания есть натуральный логарифм отношения амплитуд, отстоящих на период
. (12)
Добротность - значение фазы колебаний, при которой энергия уменьшается в e раз.
. (13)
При экспериментальном определении логарифмического декремента затухания находят логарифмы отношения амплитуды A₀ к амплитуде A_n по прошествии n колебаний:

. (14)

Добротность расчитывают по формуле (13).

Описание лабораторной установки
Лабораторная установка (рис.1) представляет собой стержень 1 с пригрузом 4, подвешенные на оси 3 (физический маятник).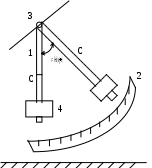

Рис.1

Для определения положения маятника имеется угломерная шкала 2. Всякое твердое тело, подвешенное на оси, не проходящей через центр масс – называется физическим маятником. Движение маятника определяется моментом силы тяжести M_m, моментом силы трения М_mp.

Согласно основному уравнению динамики вращательного движения
,
где J - момент инерции маятника относительно оси вращения, в - угловое ускорение. Подставляя выражение для момента силы тяжести и трения, получаем:
(15)
т.е. уравнение типа (7) при ,

В результате к движению маятника применима теория, рассмотренная выше, при
.

Если вся масса маятника сосредоточена в центре масс, получаем математический маятник с моментом инерции . Для него
,
где а - длина маятника

Порядок выполнения работы

1.Вывести маятник из положения равновесия, отклонив его на угол 15 – 20 градусов и записать начальное значение амплитуды А₀.

2.Отпустить маятник одновременно включив секундомер. По завершении n = 20 колебаний остановить секундомер и определить по угломерной шкале амплитуду колебания A_n. Результаты отсчета времени и амплитуды занести в таблицу 1.

3.Повторить измерения 5 раз.
Таблица 1

№ п/п	n	t(c)	t	t2	Ao	Ao	Ao2	An	An	An2
1
2
3
4
5

4.Рассчитать средние значения , , .

5.Используя средние значения , , рассчитать по формулам (6), (13), (14) период колебаний, логарифмический декремент затухания и добротность.

6.Рассчитать погрешности , , по формуле погрешности прямых измерений
.
где t_n – коэффициент Стьюдента, N – число измерений,  - погрешность угломерной шкалы.

7.Рассчитать погрешности измеренных величин по формулам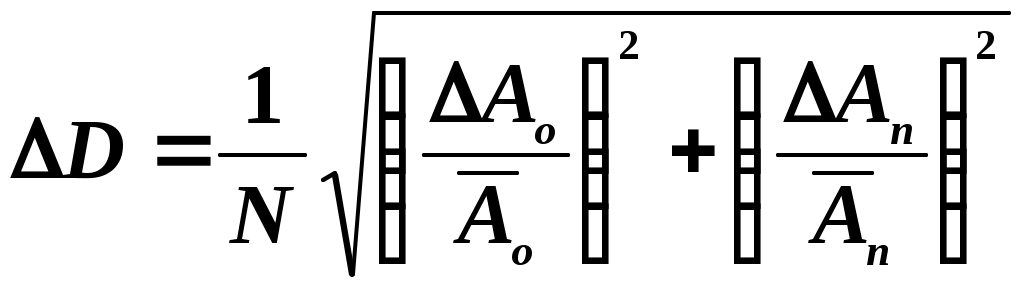
, , .
8.Записать окончательный результат для T, D и Q.

Контрольные вопросы и задания

1.Дать определение характеристик гармонического колебания.

2.Вывести формулу для энергии при гармонических колебаниях.

3.Дать определение затухающих колебаний, записать уравнение.

4.Физический смысл логарифмического декремента затухания и добротности.

5.Получить связь между добротностью и декрементом.

6.Каков физический смысл критического трения.