ФИзика. Лабораторная работа Математический маятник Цель работы изучение гармонических колебаний
 Скачать 31.95 Kb. Скачать 31.95 Kb.
|
|
[Введите текст] ываываыа Лабораторная работа 1.1. Математический маятник Цель работы: изучение гармонических колебаний, исследование зависимости периода колебаний математического маятника от его длины и определение ускорения свободного падения. Вычисление погрешностей измерений и расчётов. Теоретическая часть Гармоническими колебаниями физической величины х называется процесс изменения ее во времени t no закону x=Asin((2π/T)t+φo), где А – амплитуда колебаний; Т – период колебаний. Величина ((2π/T)t+φo), называется фаза колебаний, а соответствует фазе в начальный момент времени (t=0) и называется начальной фазой. График таких колебаний представлен на рис. 1. Из определения гармонических колебаний следует, что период колебаний является наименьшим промежутком времени, по истечении которого движение в точности повторяется.
Амплитуда колебаний А равна максимальному значению х. Величина w, называется круговой (циклической) частотой. Для изучения гармонических колебаний можно воспользоваться математическим маятником. Математический маятник – это (модель) идеализированная система, состоящая из материальной точки массой m, подвешенной на длинной нерастяжимой нити l, и совершающая колебания около положения равновесия. Математический маятник при малых углах отклонения совершает гармонические колебания с циклической частотой и периодом Т. Период колебаний маятника – это время, в течение которого маятник совершает одно полное колебание и возвращается в исходную точку. Для определения ускорения свободного падения можно воспользоваться выражением T=2π√(l/g), откуда g=4π2((l/Т2). Чтобы рассчитать ускорение свободного падения gпо этой формуле, достаточно измерить период колебаний Т по формуле T=t/n. Так как g – величина постоянная для данной географической точки, то видно, что при заданной длине маятника l период колебаний маятника Т представляет собой постоянную величину. При использовании сравнительно точного прибора можно убедиться в том, что от опыта к опыту значение tизменяется то в большую, то в меньшую сторону. Различия в результатах измерения одной и той же величины объясняются случайными погрешностями. Изучение погрешностей измерений и расчётов является одной из главных целей данной лабораторной работы. |

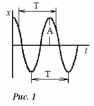
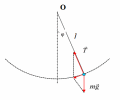 Рис.2
Рис.2