Расчет параметров склада. Лабораторные-работы. Лабораторная работа 1 Использование надстройки Поиск решения для решения задач на транспорте

• Название: Лабораторная работа 1 Использование надстройки Поиск решения для решения задач на транспорте
• Анкор: Расчет параметров склада
• Дата: 14.10.2022
• Размер: 1.61 Mb.
• Имя файла: Лабораторные-работы.doc
• Тип: Лабораторная работа; #734005
• страница: 3 из 6

2.2. Решения транспортной задачи с использованием автоматизированных систем управления

Формулировка транспортной задачи линейного программирования представлена в научных источниках [2]. В данных методических указаниях рассмотрен пример решения транспортной задачи с использованием автоматизированных систем управления [4].

Производство продукции осуществляется на четырех предприятиях, а затем развозится в 5 пунктов потребления. Предприятия могут выпускать в день 235, 175, 185 и 175 единиц продукции. Пункты потребления готовы принимать ежедневно 125, 160, 60, 250 и 175 единиц продукции. Хранение на предприятии единицы продукции обходится в 2 у. е. в день, штраф за недопоставленную продукцию – 3,5 у. е. в день. Стоимость перевозки единицы продукции (в у.е.) с предприятий в пункты потребления приведена в табл. 2.4.

Таблица 2.4 -Транспортные расходы

Предприятия		Пункты потребления
	1	2	3	4	5
1	3,2	3	2,35	4	3,65
2	3,0	2,85	2,5	3,9	3,55
3	3,75	2,5	2,4	3,5	3,4
4	4	2	2,1	4,1	3,4

Решение задачи сводится к реализации следующих этапов [4]:

1. 
   Проверка сбалансированности модели задачи. Модель является сбалансированной, т. к. суммарный объем производимой продукции в день равен суммарному объему потребности в ней:
   

235 + 175 + 185 + 175 = 125 + 160 + 60 + 250 + 175.

2. 
   Построение математической модели. Неизвестными в этой задаче являются объемы перевозок. Пусть x_ij– объем перевозок с i-го предприятия в j-й пункт потребления; a_i – объем производства на i-м предприятии; b_j – спрос в j-м пункте потребления; c_ij – стоимость перевозки единицы продукции с i-го предприятия в j-й пункт потребления. Суммарные транспортные расходы – это функционал качества (критерий цели):
   

n m

F c_ij x_ij .

i1 j1

Неизвестные в этой задаче должны удовлетворять следующим ограничениям: объемы перевозок не могут быть отрицательными; поскольку модель сбалансирована, то вся продукция должна быть вывезена с предприятий, а потребности всех пунктов потребления должны быть полностью удовлетворены. Найти минимум функционала

4 5

F c_ij x_ij  min при ограничениях

i1 j1 5

x_ij  a_i ,i1,4;

j1

4

x_ij  b_j , j1,5;

i1 x_ij  0,i1,4, j1,5.

3. Решение задачи с помощью окна Поиск решения:

• 
  подготовка рабочего листа для задачи (рис. 2.10). Формулы для расчета приведены в табл. 2.5;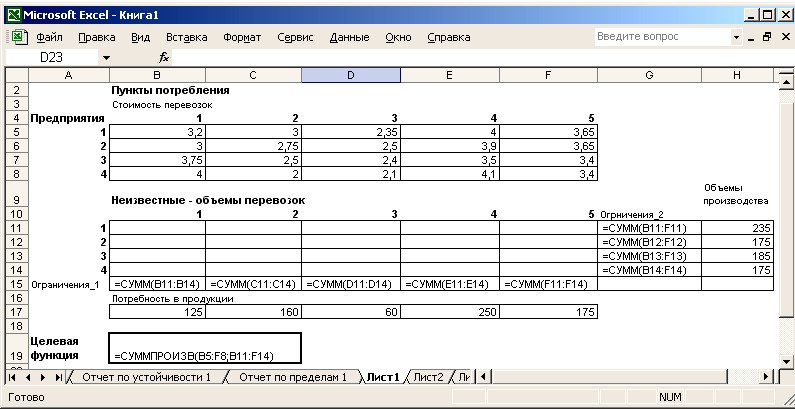
  

Рисунок 2.10 - Исходные данные для решения транспортной задачи

Таблица 2.5 - Формулы для расчета в транспортной задаче

	Описание	Ячейка	Формула
	Ограничения_1	G11	=CУMM(B11:F11)
		G12	=СУММ(В12:F2)
		G13	=СУММ(В13:F.З)
		G14	=СУММ(В14:F4)
	Ограничения_2	В15	=СУММ(В11:В14)
		С15	=СУММ(С11:С14)
		D15	=CУMM(D11:D14)
		Е15	=СУММ(Е11:Е14)
		F15	=CУMM(F11:F14)
	Целевая функция	В19	=СУММПР0ИЗВ (B5:F8;B11:F14)

• 
  ввод данных в окно Поиск решения (рис. 2.11);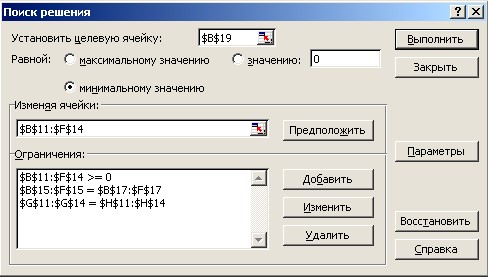
  

Рисунок 2.11 - Ввод данных в окно Поиск решения для транспортной задачи

• 
  результат решения представлен на рис. 2.12.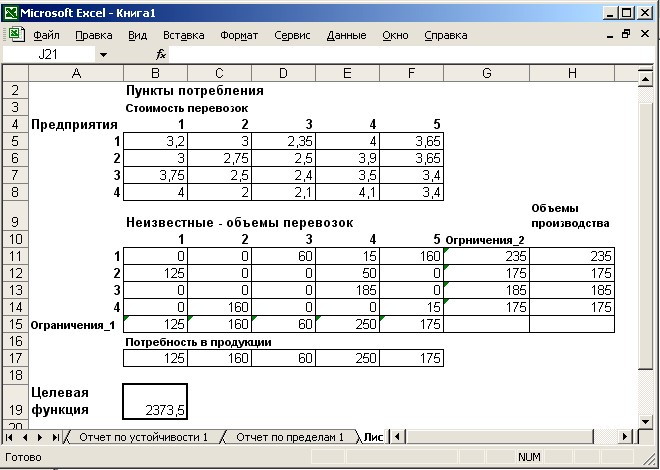
  

Рисунок 2.12 - Оптимальное решение для транспортной задачи

Задания для самостоятельного решения задач линейного программирования на транспорте

Имеются п пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции из i-го пункта производства в j-й центр потребления c_ij приведена в таблицах, где под строкой понимается пункт производства, а под столбцом – пункт потребления. Кроме того, в таблицах в i-й строке указан объем производства в i-м пункте, а в j-м столбце указан спрос в j-м центре потребления. Хранение продукции на предприятии обходится в 1,6 у.е. в день, а штраф за просроченную поставку единицы продукции, заказанной в пункте потребления, но там не хранящейся, равен 34 у.е. в сутки. Составить план перевозок по доставке требуемой продукции в пункты потребления, минимизирующий суммарные транспортные расходы. Необходимые данные для решения задач взять из соответствующих таблиц по вариантам.