Лабораторная%20работа%201%20электр. Лабораторная работа 1 Исследование электростатического поля Цели
 Скачать 1.76 Mb.
|
|
Лабораторная работа № 1 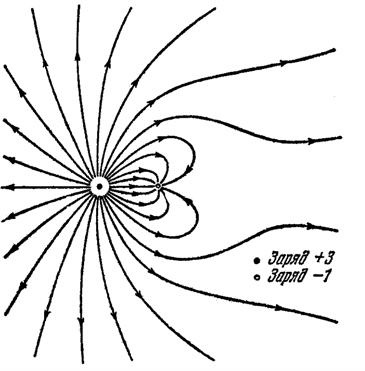 Исследование электростатического поля Цели работы: изучить метод моделирования электрических полей различной конфигурации; научиться графическому изображению моделируемых полей при помощи силовых линий и эквипотенциаль- ных поверхностей; Приборы и оборудование: источник питания 0 – 15 В; вольтметр; блок моделирования полей; сменные планшеты с различной конфигурацией элек- тродов; рисунок с координатной сеткой. Теоретическая часть Одним из основных видов взаимодействий (сил), сущест- вующих в природе, является электромагнитное. Количествен- ной мерой способности к электромагнитному взаимодействию является электрический заряд. Закон Кулона устанавливает количественное соотношение для силы взаимодействия точечных зарядов: F q1 q2 r2 , (1.1) где q1и q2– величины зарядов, r – расстояние между ними, ε - диэлектрическая проницаемость среды, а k – коэффициент про- порциональности, зависящий от выбора системы единиц. По современным представлениям взаимодействие заря- дов происходит через электрическое поле. Основные свойства электрического поля: электрическое поле возникает вокруг электрического заряда; электрическое поле действует с некоторой силой на другой заряд; Векторной силовой характеристикой электрического поля в произвольной точке является напряженность электрического   : E поля r  r E F q, (1.2) где q– величина заряда, помещенного в эту точку поля, а F - сила, действующая на этот заряд. Из (1.1) и (1.2) следует, что величина напряженности по- ля точечного заряда в произвольной точке E q r2 . (1.3) Если имеется несколько точечных зарядов, то напряженность результирующего поля равна векторной сумме напряженностей полей, создаваемых отдельными зарядами E E1E2 K Это утверждение называется принципом суперпозиции. (1.4) Графически изобразить электрическое поле позволяют силовые линии. Силовая линия – это линия, для которой на- правление касательной в любой точке совпадает с направлением вектора напряженности.  Рис.1.1 Условились силовые линии проводить так, что густота линий пропорциональна величине напряженности поля. Силовые линии электрического поля не замкнуты, они либо начинаются на положительном заряде и заканчиваются на отри- цательном заряде, либо уходят в бесконечность. Силовые линии не пересекаются друг с другом. Энергетической скалярной характеристикой электрического поля в произвольной точке является потенциал электрического поля φ. Потенциал произвольной точки поля численно равен потен- циальной энергии единичного положительного заряда в этой точке или работе, совершаемой полем, при перемещении еди- ничного положительного заряда из данной точки поля в бесконечность. 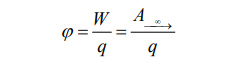 Выбор нулевого уровня потенциала (потенциальной энергии) достаточно условен и определяется удобством приме- нения. В ряде задач за нулевой уровень удобно принимать не потенциал бесконечно удаленной точки, а потенциал Земли или потенциал корпуса прибора. Потенциал поля точечного заряда в произвольной точке рассчитывается по формуле k q 1   (1.6) r При перемещении заряда q из точки поля с потенциалом φ1в точку с потенциалом φ2электрические силы совершают ра- боту А, причем   A 1 2 q , (1.7) где φ1- φ2– разность потенциалов. Таким образом, работа сил электростатического поля определяется только начальной и конечной точками и не зависит от формы траектории. При перемещении заряда по замкнутой траектории рабо- та сил электростатического поля равна нулю. Такие поля (и силы) называются консервативными или потенциальными. Можно графически изображать электрическое поле при помощи эквипотенциальных поверхностей (как и с помощью си- ловых линий). Эквипотенциальная поверхность – геометриче- ское место точек, имеющих одинаковый потенциал. Можно по казать, что в любой точке поля эквипотенциальная поверх- ность перпендикулярна вектору напряженности или силовой линии. Таким образом, по эквипотенциальным поверхностям можно построить силовые линии и наоборот. Для произвольного направления l в любой точке поля по- тенциал и напряженность связаны соотношением: 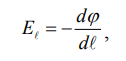 1.8где El– проекция вектора на направление l. Т.к. (1.8) справедливо для любого направления, то можно показать, что 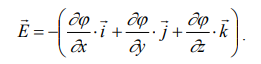 1.9Величина, стоящая в скобках называется градиент потенциала и обозначается grad φ. Таким образом E grad , (1.10) т.е. вектор E направлен в сто- рону наиболее быстрого убы- вания потенциала (рис.1.2). 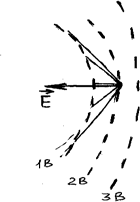 Практическая часть Справа: 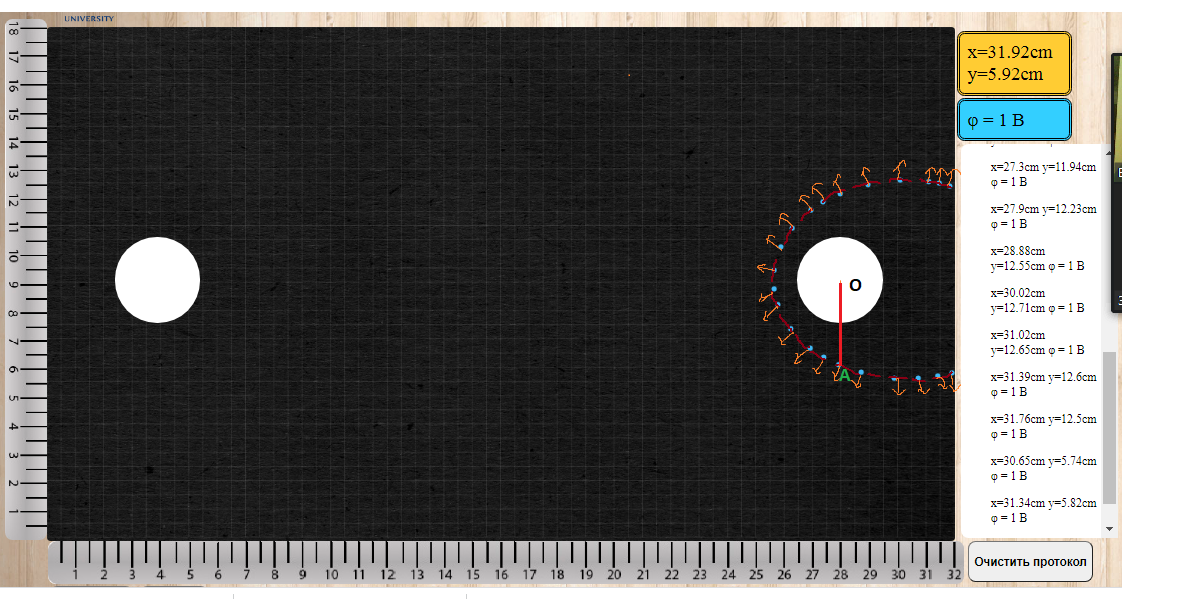 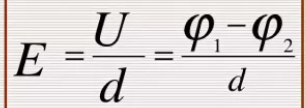 D=ОA=3 см= 3*10-2м E(A)=1В/(3*10-2м)=33,3 В/м Слева: 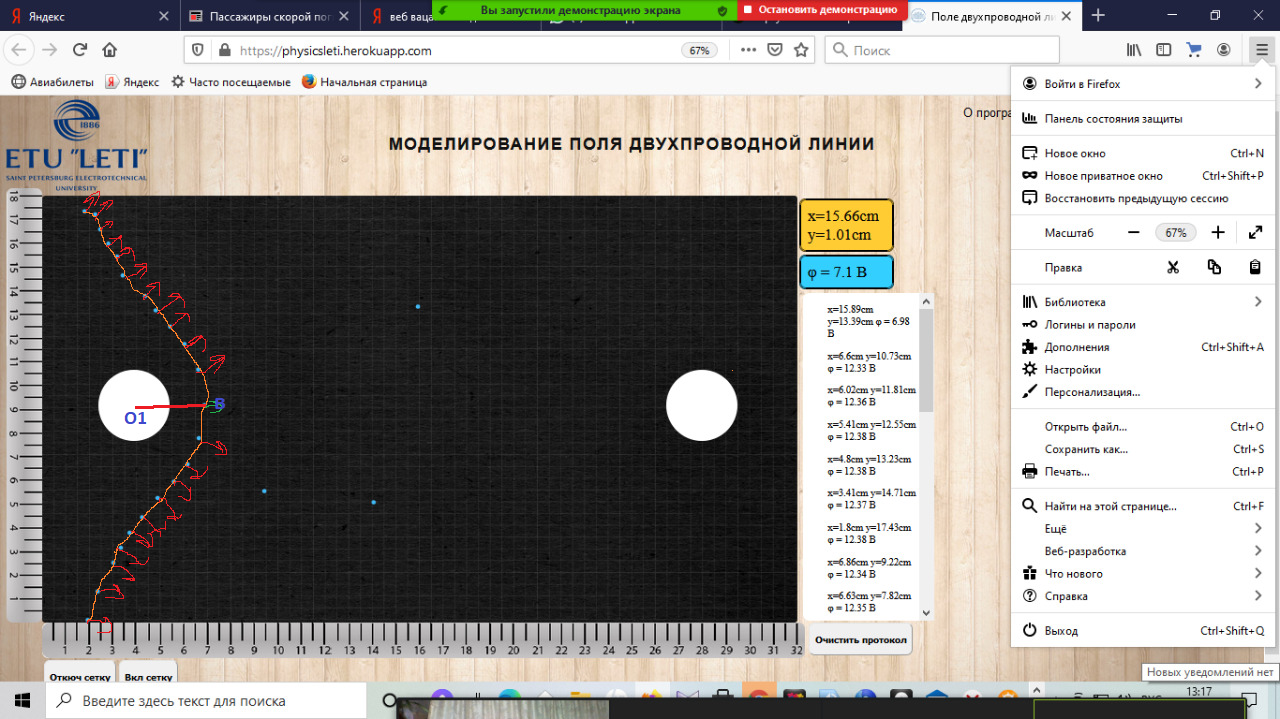 D1=О1В=3 см= 3*10-2м E(B)=12,3В/(3*10-2м)=410 В/м Вывод : В ходе данной лабораторной работы мы изучили методы моделирования электрических полей различной конфигурации, научились графическому изображению моделируемых полей при помощи силовых линий и эквипотенциальных поверхностей. Ответ на контрольные вопросы: 2. 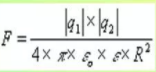 Т.к. изначально диэлектрическая проницаемость в вакумме была равна 1,то после диэлектрическая проницаемость равна 2.То есть увеличилась в 2 раза, а Сила взаимодействия обратнопропорциональна диэлектрической проницаемости, значит Сила уменьшится в 2 раза.Если увеличить расстояние в два раза (R1=2R),то Сила взаимодействия уменьшится в 4 раза.Если брать в совокупности два изменения,то сила взаимодействия точечных зарядов уменьшится в 8 раз. 9.Силовые линии пересекаться не могут,так как в каждой точке поля его напряженность имеет одно единственное значение и определенное направление. Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных. |