Лабораторная работа 1 Исследование разомкнутой линейной системы (краткие теоретические сведения) Модели линейных систем
 Скачать 347.5 Kb.
|
|
Исследование САУ с помощью среды Scilab Лабораторная работа № 1Исследование разомкнутой линейной системы(краткие теоретические сведения)Модели линейных систем Для описания линейных систем могут применяться несколько способов: дифференциальные уравнения модели в пространстве состояний передаточные функции модели вида «нули-полюса» Первые два способа называются временныَми, поскольку описывают поведение системы во временной области и отражают внутренние связи между сигналами. Передаточные функции и модели вида «нули-полюса» относятся к частотным способам описания, так как непосредственно связаны с частотными характеристиками системы и отражают только вход-выходные свойства (то есть, описывают динамику не полностью). Частотные методы позволяют применять для анализа и синтеза алгебраические методы, что часто упрощает расчеты. С другой стороны, для автоматических вычислений более пригодны методы, основанные на моделях в пространстве состояний, поскольку они используют вычислительно устойчивые алгоритмы линейной алгебры. Исходные уравнения динамики объектов, которые строятся на основе законов физики, имеют вид нелинейных дифференциальных уравнений. Для приближенного анализа и синтеза обычно проводят их линеаризацию в окрестности установившегося режима и получают линейные дифференциальные уравнения. Линейное уравнение  можно записать в операторной форме или  где  – входной сигнал,  – сигнал выхода,  – оператор дифференцирования,  и  – операторные полиномы.Передаточная функция  линейной стационарной системы от комплексной переменной  определяется как отношение преобразования Лапласа выхода к преобразованию Лапласа входа при нулевых начальных условиях Передаточная функция звена, которое описывается приведенным выше уравнением, равна  ,то есть, совпадает с отношением операторных полиномов  при замене переменной  на .Передаточная функция в среде Scilab вводится в виде отношения двух многочленов (полиномов) от комплексной переменной s. Полиномы хранятся как массивы коэффициентов, записанных по возрастанию степеней. Например, передаточная функция  вводится следующим образом1 --> n = poly([4 2], 's', 'coeff') n = 4 + 2s Второй параметр ('s') обозначает переменную, а третий ('coeff') показывает, что массив задаёт коэффициенты полинома (а не его корни). В отличие от Matlab, коэффициенты полинома вводятся в обратном порядке – от младшего к старшему. Можно было использовать встроенную переменную %s: --> s = %s --> n = 2*s + 4 n = 4 + 2s --> d = s^3 + 1.5*s^2 + 1.5*s + 1 d = 1 + 1.5s + 1.5s^2 + s^3 --> f = syslin('c', n, d) 4 + 2s ----------------------- 1 + 1.5s + 1.5s^2 + s^3 или сразу, без предварительного построения числителя и знаменателя: --> f = syslin('c', 2*s+4, s^3+1.5*s^2+1.5*s+1 ); В памяти создается объект, описывающий передаточную функцию. Точка с запятой в конце команды подавляет вывод на экран. С помощью функции roots можно найти нули и полюса передаточной функции: --> z = roots ( n ) - 2. --> p = roots ( d ) - 0.25 + 0.9682458i - 0.25 - 0.9682458i - 1. Нулями называются корни числителя, полюсами – корни знаменателя. Эта функция имеет один нуль в точке  и три полюса в точках  и  . Паре комплексных полюсов соответствует квадратный трехчлен.Модель в пространстве состояний связана с записью дифференциальных уравнений в стандартной форме Коши (в виде системы уравнений первого порядка):  Здесь  – вектор переменных состояния размера  ,  – вектор входных сигналов (вектор управления) размера  и  – вектор выходных сигналов размера  . Кроме того,  ,  ,  и  – постоянные матрицы. Согласно правилам матричных вычислений, матрица должна быть квадратной размера  , матрица имеет размер  , матрица –  и матрица –  . Для систем с одним входом и одним выходом2 матрица – скалярная величина.Для преобразования передаточной функции в модель в пространстве состояний используется команда --> f_ss = tf2ss ( f ) f_ss(2) = A matrix = x1 x2 x3 x1 -1.5 -0.1875 -0.03125 x2 8 0 0 x3 0 4 0 f_ss(3) = B matrix = u1 x1 0.5 x2 0 x3 0 f_ss(4) = C matrix = x1 x2 x3 y1 0 0.5 0.25 f_ss(5) = D matrix = u1 y1 0 Это означает, что матрицы модели имеют вид 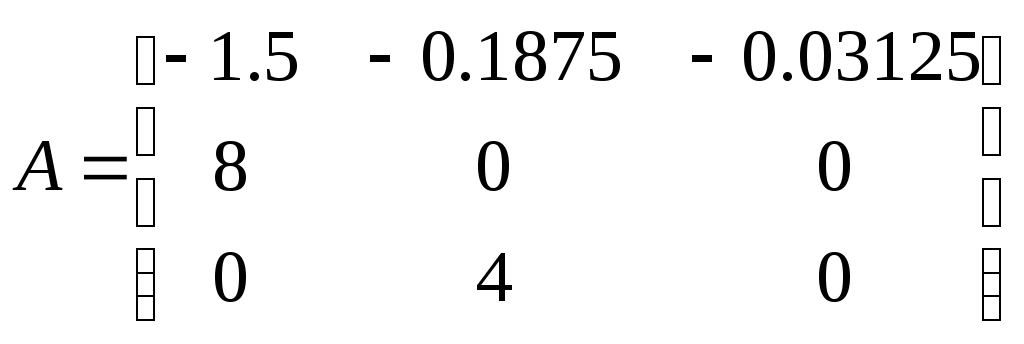 ,  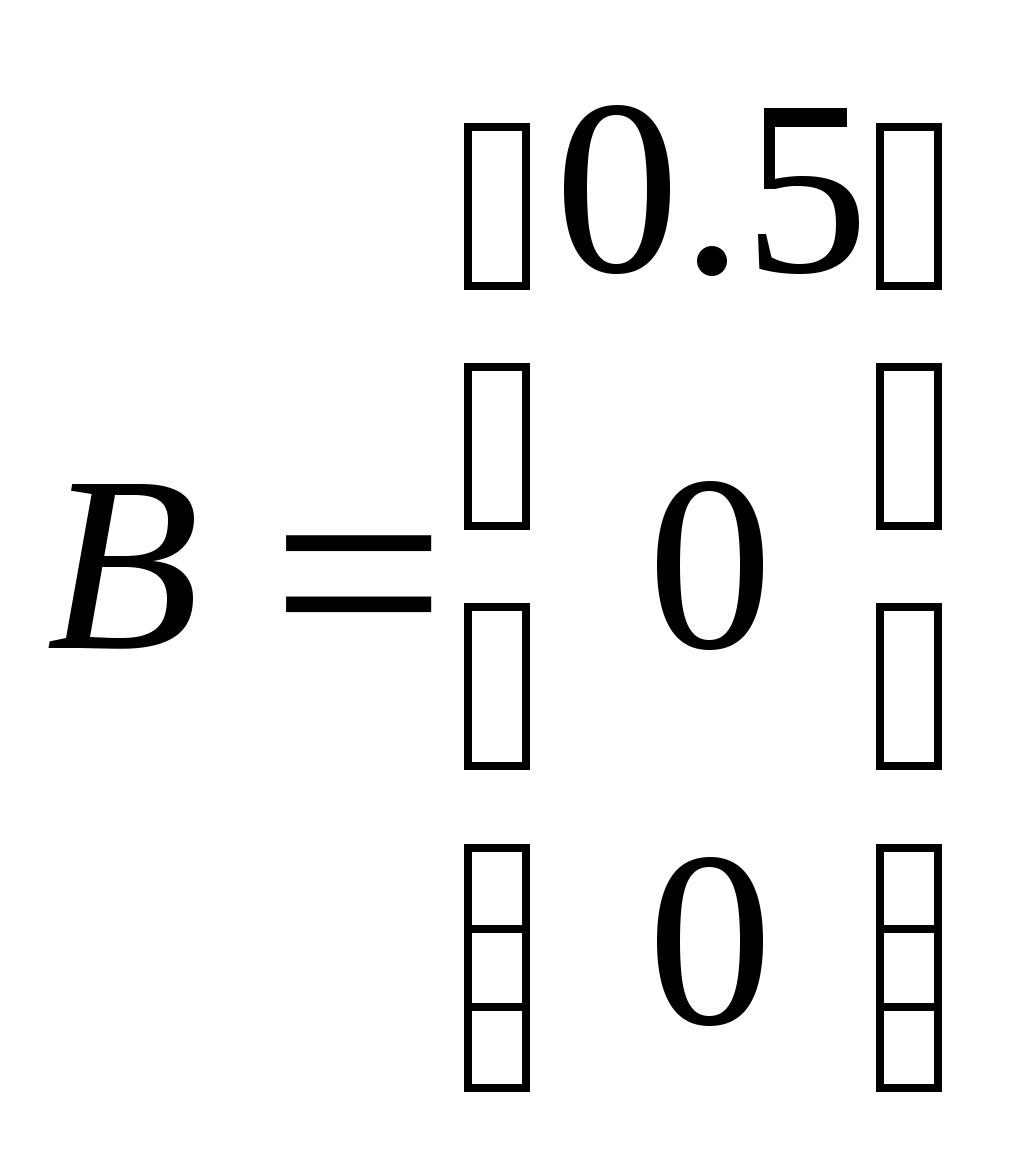,  ,  .Модель в пространстве состояний можно построить не для всех передаточных функций, а только для правильных, у которых степень числителя не выше, чем степень знаменателя. Например, передаточная функция  – неправильная, она не может быть преобразована в модель в пространстве состояний. Используют также понятие строго правильной функции, у которой степень числителя меньше, чем степень знаменателя. Если построить модель в пространстве состояний для такой функции, матрица будет равна нулю, то есть, прямая передача с входа на выход отсутствует (при скачкообразном изменении входа сигнал на выходе будет непрерывным).Коэффициент усиления в установившемся режиме Одна из важнейших характеристик линейной системы – коэффициент усиления в установившемся режиме или статический коэффициент усилении(staticgain, DC-gain). Его можно определить как установившееся значение сигнала выхода при постоянном входном сигнале, равном единице. Размерность этой величины равна отношению размерностей сигналов выхода и выхода. Рассмотрим дифференциальное уравнение .Полагая все производные (в установившемся режиме) равными нулю, получаем  .Статический коэффициент усиления равен  .Если задана передаточная функции, для вычисления  надо подставить в нее  , поскольку переменная соответствует оператору дифференцирования. Рассмотренному выше уравнению можно сопоставить передаточную функцию .Тогда  .Если система содержит интегрирующее звено (передаточная функция имеет полюс в точке ), этот предел равен бесконечности, то есть, при постоянном сигнале выход бесконечно увеличивается или уменьшается, не достигая установившегося режима.Тот же результат можно получить с помощью эквивалентной модели в пространстве состояний. С помощью среды Scilab находим  .Полагая  , получаем модель, определяющую установившийся режим    ,откуда следует  .Для нашей системы, как и раньше, получаем  . Заметьте, что для того, чтобы статический коэффициент усиления был конечен, требуется обратимость матрицы , то есть, отсутствие интегрирующих звеньев3. Чтобы найти статический коэффициент усиления модели f в Scilab, используется команда --> k = horner ( f, 0 ) // подставить s = 0 Импульсная характеристика Импульсной характеристикой (весовой функцией)  называется реакция системы на единичный бесконечный импульс (дельта-функцию или функцию Дирака) при нулевых начальных условиях. Дельта-функция  определяется равенствами ,  .Это обобщенная функция – математический объект, представляющий собой идеальный сигнал, никакое реальное устройство не способно его воспроизвести. Дельта-функцию можно рассматривать как предел прямоугольного импульса единичной площади с центром в точке  при стремлении ширины импульса к нулю. Второе название – весовая функция – связано с тем, что для произвольного входного сигнала выход системы вычисляется как свертка .Здесь функция как бы «взвешивает» входной сигнал в подынтегральном выражении.Импульсная характеристика отражает лишь вход-выходные соотношения при нулевых начальных условиях, то есть, не может полностью описывать динамику системы. Понятие импульсной характеристики используется главным образом для систем, передаточные функции которых строго правильные. Если передаточная функция правильная, но не строго правильная, коэффициент прямой передачи с входа на выход (матрица модели в пространстве состояний) не равен нулю, поэтому бесконечный импульс на входе в момент  передается на выход. Такую (бесконечную по величине) импульсную характеристику невозможно построить. Система Scilab в этом случае просто добавляет значение D к импульсной характеристике строго правильной части (для которой ), то есть «поднимает» импульсную характеристику на величину D. Это один из тех случаев, когда компьютер выдает качественно неверный результат.Если система не содержит интеграторов, импульсная характеристика стремится к нулю. Это следует из теоремы о предельном значении:  ,где – передаточная функция системы, которая является преобразованием Лапласа для . Импульсная характеристика системы с одним интегратором стремится к постоянной величине, равной статическому коэффициенту передачи системы без интегратора. Для системы с двумя интеграторами импульсная характеристика асимптотически стремится к прямой, с тремя интеграторами – к параболе и т.д.Переходная характеристика Переходной характеристикой(переходной функцией)  называется реакция системы (при нулевых начальных условиях) на единичный ступенчатый сигнал (единичный скачок)   . Импульсная и переходная функции связаны выражениями  ,  .Для систем без интеграторов переходная характеристика стремится к постоянному значению. Переходная характеристика системы с дифференцирующим звеном (числитель передаточной функции имеет нуль в точке ) стремится к нулю. Если система содержит интегрирующие звенья, переходная характеристика асимптотически стремится к прямой, параболе и т.д., в зависимости от количества интеграторов.По определению предельное значение переходной функции при  есть статический коэффициент усиления: .Эта величина имеет смысл только для устойчивых систем, поскольку при неустойчивости переходный процесс не сходится к конечному значению. Е  сли передаточная функция правильная, но не строго правильная (матрица модели в пространстве состояний не равна нулю), скачкообразное изменение входного сигнала мгновенно приводит к скачкообразному изменению выхода. Величина этого скачка равна отношению коэффициентов при старших степенях числителя и знаменателя передаточной функции (или матрице модели в пространстве состояний).П  о переходной характеристике можно найти важнейшие показатели качества системы – перерегулирование (overshoot) и время переходного процесса (settlingtime).Перерегулированиеопределяется как  ,где  – максимальное значение функции , а  – установившееся значение выхода. Если установившееся значение отрицательное, при вычислении перерегулирования нужно выполнить «зеркальное отражение» сигналов – поменять знаки у  и  . В формуле вместо максимального значения нужно взять минимальное: .Время переходного процесса – это время, после которого сигнал выхода отличается от установившегося значения не более, чем на заданную малую величину (обычно 2% или 5% от установившегося значения). Частотная характеристика При подаче на вход линейной системы гармонического (синусоидального) сигнала  с частотой  (она измеряется в радианах в секунду), на выходе будет также гармонический сигнал той же частоты, но другой амплитуды и фазы4  , где – амплитуда и  – сдвиг фазы.Частотная характеристика определяется как реакция системы на комплексный экспоненциальный сигнал  . Для ее построения надо использовать подстановку  в передаточной функции . Выражение  называется частотной передаточной функцией или амплитудно-фазовой частотной характеристикой системы (АФЧХ).Зависимость модуля величины от частоты называется амплитудной частотной характеристикой (АЧХ), а зависимость аргумента комплексного числа (фазы) от частоты – фазовой частотной характеристикой (ФЧХ): .АЧХ показывает, насколько усиливается амплитуда сигналов разных частот после прохождения через систему, а ФЧХ характеризует сдвиг фазы сигнала.           Реальные объекты имеют строго правильную передаточную функцию, поэтому их АЧХ убывает с ростом частоты и асимптотически стремится к нулю. Говорят, что такой объект обладает свойством фильтра – фильтрует (не пропускает) высокочастотные сигналы (помехи, шумы измерений). Это свойство служит основой для использования метода гармонического баланса. Максимум АЧХ соответствует частоте, на которой усиление наибольшее. Значение АЧХ при  равно усилению при постоянном сигнале, то есть, статическому коэффициенту усиления  . Это следует и из равенства .Для систем с интегрирующими звеньями частотная характеристика стремится к бесконечности при  . Это значит, что их выход бесконечно увеличивается или уменьшается при постоянном входном сигнале.Частота, после которой значение АЧХ уменьшается ниже 0 дБ (коэффициент усиления меньше 1, сигнал ослабляется), называется частотой среза системы  .Чтобы построить частотные характеристики в Scilab, надо сначала создать массив частот в нужном диапазоне. Для этого можно использовать функции linspace (равномерное распределение точек по линейной шкале) и logspace (равномерное распределение точек по логарифмической шкале). Команда >> w = linspace (0, 10, 100); строит массив из 100 точек с равномерным шагом в интервале от 0 до 10, а команда >> w = logspace (-1, 2, 100); – массив из 100 точек с равномерным шагом по логарифмической шкале в интервале от  до  .Частотная характеристика на сетке w для линейной модели f (заданной как передаточная функция, модель в пространстве состояний или в форме «нули-полюса») вычисляется с помощью функции repfreq: >> fResp = repfreq(f, w/(2*%pi)); Функция repfreq принимает два аргумента: модель системы и массив частот в герцах. Поскольку массив w – это угловые частоты ( = 2f), для получения массива «обычных» частот нужно разделить все значения на 2. Дальше можно найти модуль частотной характеристики: >> Aw = abs(fResp); Для вывода графика АЧХ на экран можно использовать команду Scilab >> plot2d ( "ln", w, Aw ) Первый аргумент «ln» говорит о том, что используется логарифмический масштаб по оси абсцисс (частот). Для вычисления фазы в градусах используется команда >> phi = phasemag(fResp); после чего можно строить ФЧХ, например: >> plot2d ( "ln", w, phi ); Частота, при которой мощность сигнала (данной частоты) после прохождения через систему падает в 2 раза, называется полосой пропускания системы . На этой частоте коэффициент усиления равен  ( – статический коэффициент усиления), то есть значение АЧХ равно –3 дБ ( 0,708 от её значения при  ).Найдем коэффициент усиления, равный -3 дБ: >> k3dB = 10^(-3/20); Найдём индексы массива значений АЧХ, для которых коэффициент усиления не меньше -3 дБ от значения Aw(1) (при нулевой частоте): >> ind = find(Aw >= k3dB*Aw(1)); Полосу пропускания вычислим как максимальную частоту, для которой коэффициент усиления больше или равен -3дБ: >> B = max( w(ind) ); Полюса и нули Многие динамические свойства системы (например, быстродействие и колебательность переходного процесса) определяются полюсами передаточной функции (или, что то же самое, собственными числами матрицы модели в пространстве состояний). Передаточную функцию можно записать как произведение передаточных функций элементарных звеньев первого и второго порядков. Таким образом, множество полюсов передаточной функции устойчивой системы составляют полюса передаточных функций двух типов простейших звеньев: апериодических и колебательных. Апериодическое звено с передаточной функцией вида  имеет единственную характеристику – постоянную времени  . Начиная примерно с частоты5  , АЧХ такого звена начинает убывать, приближаясь к нулю.Колебательное звено имеет передаточную функцию  , где – постоянная времени и  . Частота называется собственной частотой (naturalfrequency), а параметр  – параметром затухания или коэффициентом демпфирования (dampingfactor). При уменьшении импульсная и переходная функции приобретают ярко выраженный колебательный характер, а на АЧХ появляется «горб» в районе частоты  . В предельном случае при  колебания становятся незатухающими, а звено называется консервативным. С другой стороны при  корни знаменателя становятся вещественными, и звено превращается в апериодическое звено второго порядка.Для нахождения полюсов передаточной функции f можно использовать функцию >> p = roots(denom(( f ))) Вызов функции >> [w0,zeta,p] = damp ( f ) позволяет найти не только полюса p, но также соответствующие им собственные частоты w0 и коэффициенты демпфирования zeta в виде массивов. Нули передаточной функции f вычисляются как >> z = roots(numer(( f )); Устойчивость системы не зависит от расположения нулей, но они существенно влияют на переходные процессы. Команда >> plzr ( f ); строит карту расположения нулей (они обозначаются кружками) и полюсов (крестики) системы на комплексной плоскости. 1 Черным цветом обозначается ввод пользователя, синим – ответ среды Scilab. 2 В зарубежной литературе для одномерных систем используется сокращение SISO = SingleInputSingleOutput. 3 Полюса передаточной функции являются собственными числами матрицы . Таким образом, если у передаточной функции есть полюс в точке  , матрица будет вырожденной.4 Для нелинейных систем это неверно. 5 Значение возвращается функцией damp как собственная частота для вещественного полюса. |