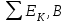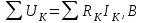ТОЭ лр1. ЛР 1. Лабораторная работа 1 Исследование разветвленной линейной электрической цепи постоянного тока с двумя источниками электрической энергии

• Название: Лабораторная работа 1 Исследование разветвленной линейной электрической цепи постоянного тока с двумя источниками электрической энергии
• Анкор: ТОЭ лр1
• Дата: 06.10.2022
• Размер: 93.19 Kb.
• Имя файла: ЛР 1.docx
• Тип: Лабораторная работа; #719216

Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования

Уфимский Государственный Авиационный Технический Университет

Кафедра ТОЭ
ЛАБОРАТОРНАЯ РАБОТА № 1

Исследование разветвленной линейной электрической цепи постоянного тока с двумя источниками электрической энергии

Вариант 11

Выполнил: студент группы

.

Проверил: доцент кафедры ТОЭ

.

Уфа-2020

Цель работы:

Экспериментальная проверка законов Кирхгофа и основных свойств линейных цепей постоянного тока.

Описание установки:

Лабораторная работа выполняется на универсальном лабораторном стенде «Квазар».

При сборке электрических цепей используется следующее оборудование: – регулируемые источники постоянного напряжения БП-15;

– R1, R2, R3 – переменные резисторы 220 Ом «Блока нагрузок»; «Блок контроля тока»;

– электронный вольтметр и амперметр «Блока измерительных приборов».

Практическая часть: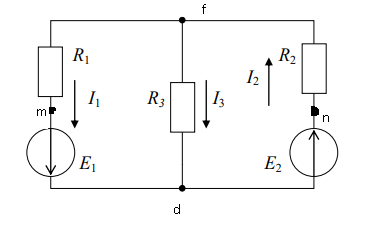





Рисунок 1- Схема разветвленной цепи постоянного тока

Проверка первого закона Кирхгофа:

Алгебраическая сумма токов в ветвях, подключенных к любому узлу

электрической цепи, равна нулю. Для заполнения таблицы измерим токи I₁, I₂, I₃, а также определим их направление. Все полученные значения запишем в таблицу.

Таблица 1. 1

Измерено			Вычислено
I1, A	I2, A	I3, A	, A
0,080	0,152	0,071	0,001

Пример расчета: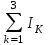

= -I₁₊I₂-I₃= -0,080+0,152-0,071 = 0,001 A

Проверка второго закона Кирхгофа:

Считая потенциал одного узла электрической цепи равным нулю, измерим потенциалы всех других узлов вольтметром. Данные измерения занесем в табл. 1.2. Произведя соответствующие расчеты, проверим выполнение второго закона Кирхгофа для внешнего и любого другого контура.

Таблица 1. 2

Измерено				Вычислено
d, В	m, В	f, В	n, В
0	-10	2,82	15,1		25	24,96
					10	9,96

Пример расчета:

1. 
   для внешнего контура:
   

R₁ I₁ + R₂ I₂= E₁ + E₂

160*0,080+80*0,152 = 10 + 15

2) для внутреннего контура:

R₁ I₁ – R₃ I₃ = E₁

160*0,080-40*0,071 = 10

Чтобы построить диаграмму я буду использовать ход по часовой стрелке.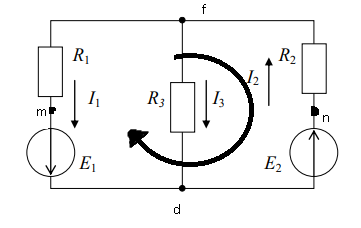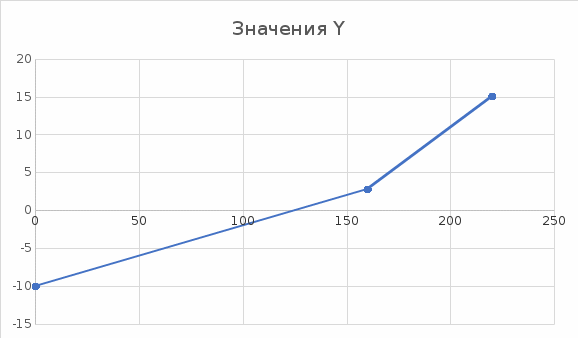





Потенциальная диаграмма для внешней цепи:



Вывод: в ходе экспериментов выяснилась справедливость первого и второго закона Кирхгофа

Проверка принципа наложения:

Ток в любой ветви электрической цепи, находящейся под воздействием нескольких источников электрической энергии, равен алгебраической сумме частичных токов, вызываемых каждым источником в отдельности. Принцип наложения справедлив и для напряжения.

Результаты опыта запишите в табл. 1.3. Рассчитаем реальные токи по методу наложения и убедимся в выполнении первого закона Кирхгофа.

Таблица 1. 3

Измерено								Вычислено
	I1, А	I1, А	I2, А	I2, А	I3, А	I3, А	Ik, А		Ik, А
E1	0,055	-	0,018	-	-0,036	-	-0,001		-
E2	-	0,030	-	0,130	-	0,108	-		-0,008
Ik = Ik + Ik	0,215		0,406		0,192		0

Пример расчета:

Σ_I = -I₁ +I₂ - I₃ = (-0,055) + 0,018 - (-0,036) ≈ -0,001 А

Σ_I = -I₁ + I₂ - I₃ = (-0,030) + 0,130 - 0,108 ≈ -0,008 А;

I = I + I;

I₁ = 0,055 + 0,030 = 0,085 А;

I₂ = 0,018 + 0,130 = 0,148 А;

I₃ = -0,036 + 0,108 = 0,072 А;

Σ_I = -I1 + I2 - I3 – первый закон Кирхгофа

Σ_I = 0,085 - 0,148 + 0,072 = 0,009 ≈ 0 А

Вывод: в ходе опыта выяснили, что ток в K ветви равен алгебраической сумме токов, вызываемых в этой ветви каждой ЭДС, то есть справедливость принципа наложения.

Определение входных и взаимных проводимостей цепи:

Пример расчета:

G₁₁=I₁/E₁= (0,080/10) = 0,008

G₂₂=I₂/E₂= (0,152/15) = 0,0101

G₁₂=I₂/E₁= (0,152/10) = 0,0152

G₁₃=I₃/E₁= (0,071/10) = 0,0071

G₂₃=I₃/E₂= (0,071/15) = 0,0047

Проверка теоремы об эквивалентном генераторе:

Любая сложная линейная цепь по отношению к выделенной ветви может быть представлена активным двухполюсником с эквивалентной ЭДС E_ЭГ и внутренним сопротивлением R_ВН, причем ЭДС E_ЭГ равна напряжению на зажимах разомкнутой ветви (напряжению холостого хода), а сопротивление R_ВН равно входному сопротивлению соответствующего пассивного двухполюсника со стороны зажимов, к которым подключена указанная ветвь.

Данные опыта запишем в табл. 1.4. Вычислим внутреннее

сопротивление R_ВН и ток I₃ по методу эквивалентного генератора.

Таблица 1. 4

Измерено		Вычислено
UХХ=ЕЭГ, В	IКЗ, А	RВН= UХХ / IКЗ Ом	I3= UХХ / (RВН +R3), А
6,7	0,129	51,93	0,1

Пример расчета:

R_ВН= U_ХХ / I_КЗ= 6,7 / 0,129 ≈ 51,93 Ом

I₃= U_ХХ / R_ВН +R₃ = 6,7 / (51,93 + 15) ≈ 0,1 А

Вывод: в ходе опыта получили те же значения тока, что и в предыдущих опытах, следовательно, метод эквивалентного генератора справедлив.

Вывод:

В ходе выполнения лабораторной работы я проверил экспериментально 1-ый и 2-ой закон Кирхгофа, определил входные и взаимные проводимости цепи, рассмотрел принципы наложения, теорему об эквивалентном генераторе. Выяснил, что алгебраическая сумма токов ветвей в любом узле электрической цепи = 0. Собрал электрическую цепь, с помощью метода вольтметра–амперметра установил сопротивления по заданным значениям, а также определил величину тока в цепи при заданном значении сопротивления резистора, выставил любое удобное значение ЭДС в диапазоне от 0 до 15 В. Для внешнего контура построил потенциальную диаграмму. Для постройки диаграммы я придерживался правилу: ток через резистор всегда направлен от большего потенциала к меньшему. Все данные проверил и записал в соответствующие таблицы.