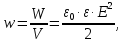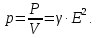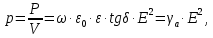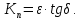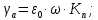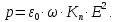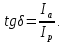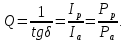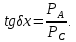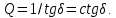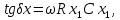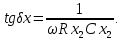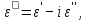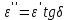лаба. 1 лаба. Лабораторная работа 1 Изучение свойств проводников. Определение удельного сопротивления проводника Цели работы
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
Диэлектрическая проницаемость и электрические поля в диэлектрикахОпределение диэлектрической проницаемости приводилось еще в школьной программе. Не вдаваясь в детали, ее проще определить через заряд плоского конденсатора. Если взять плоский конденсатор в вакууме, то зарядQ0 на каждой его пластине равен (по модулю):
Соответственно ёмкость
где ε0 = 8,85 · 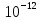 Ф/м – диэлектрическая постоянная, или диэлектрическая Ф/м – диэлектрическая постоянная, или диэлектрическая проницаемость вакуума; S – площадь каждой из пластин; d – зазор между пластинами; U – напряжение между пластинами. Разделив на площадь и перейдя к плотности заряда на обкладке σ, получим
В подключенном конденсаторе напряжение между пластинами принудительно поддерживается, но заряд на каждой пластине увеличивается до нового значения Сх. Отношение
называется диэлектрической проницаемостью материала. Из самого определения видно, что диэлектрическая проницаемость материала является безразмерной величиной. Перейдя к плотности заряда на обкладке, в случае диэлектрика получим:
Диэлектрические потериПотери в диэлектриках наблюдаются как при переменном напряжении, так и при постоянном, поскольку в материале обнаруживается сквозной ток при постоянном напряжении, когда нет периодической поляризации. Качество материала характеризуется значениями удельных объемного и поверхностного сопротивлений. При переменном напряжении необходимо использовать другую характеристику качества материала, так как в этом случае, кроме сквозного тока, возникают дополнительные причины, вызывающие потери в диэлектрике. Диэлектрические потери по их особенностям и физической природе подразделяются на четыре основных вида: диэлектрические потери, обусловленные поляризацией; диэлектрические потери, обусловленные сквозной электропроводностью; ионизационные диэлектрические потери; диэлектрические потери обусловленные неоднородностью структуры. В идеальном диэлектрике (без потерь) энергия электростатического поля может только накапливаться и сохраняться равной w (в расчёте на единицу объема):
где Е – напряженность электростатического поля; γ – удельная проводимость диэлектрика. В реальном диэлектрике часть энергии рассеивается, превращаясь в другой вид энергии, а именно в теплоту. В диэлектриках есть два основных механизма превращения энергии в тепло: потери за счет проводимости и поляризационные потери. Удельные потери проводимости (удельная тепловая мощность тока) при постоянном напряжении определяются по закону Джоуля - Ленца в дифференциальной форме:
Удельная проводимость диэлектриков на постоянном токе крайне незначительна, поэтому и потери энергии оказываются пренебрежимо малыми по сравнению с потерями на переменном токе. Для случая переменного напряжения появляются потери, связанные с поляризацией и токами абсорбции, которые принято представлять в виде удельной активной мощности:
где γа– активная составляющая удельной проводимости. Как следует из последнего выражения, удельная активная мощность p оказывается пропорциональной произведению ε·tgδ, которое называют коэффициентом диэлектрических потерь Кп:
Учитывая выражения для Кп , величины γа и p представим в следующем виде:
Таким образом, удельная активная мощность потерь p пропорциональна частоте ω, квадрату напряжённости поля Е и коэффициенту диэлектрических потерь Кп , учитывающему влияние диэлектрической проницаемости ε и тангенса угла диэлектрических потерь tgδ. Такая форма представления величины p удобна для раздельной оценки влияния характеристик поля (ω, Е) и свойств диэлектрика (ε, tgδ) на величину удельной активной мощности потерь. Физический смысл тангенса угла диэлектрических потерь становится ясным, если обратиться к векторной диаграмме, изображенной на рисунке 2.2, б. Из этой диаграммы следует, что
Таким образом, tgδ – это отношение активной и реактивной составляющих тока, возникающих под действием переменного (синусоидального) напряжения, приложенного к образцу диэлектрика. Так как оба элемента схемы замещения (R и C) находятся под одинаковым напряжением, то отношение мощностей этих элементов оказывается равным отношению токов, протекающих через них. Поэтому тангенс угла потерь показывает, какую часть от реактивной мощности составляет мощность активных потерь. Применяется и другое понятие - добротность изоляции, определяемое соотношением:
Физически угол диэлектрических потерь – угол, дополняющий до 90° угол фазового сдвига между током и напряжением в емкостной цепи. Для идеального диэлектрика вектор тока в такой цепи будет опережать вектор напряжения на 90°, при этом угол диэлектрических потерь δ будет равен нулю. Чем больше рассеиваемая в диэлектрике мощность, переходящая в теплоту, тем меньше угол фазового сдвига и тем больше угол и его функция tgδ. Недопустимо большие диэлектрические потери в электроизоляционном материале вызывают сильный нагрев изготовленного из него изделия и могут привести к его тепловому разрушению. Даже если напряжение, приложенное к диэлектрику, недостаточно велико для того, чтобы за счет диэлектрических потерь мог произойти недопустимый перегрев, то и в этом случае большие диэлектрические потери могут принести существенный вред, увеличивая, например, активное сопротивление колебательного контура, в котором использован данный диэлектрик, а, следовательно, и величину затухания. Природа диэлектрических потерь в электроизоляционных материалах различна в зависимости от агрегатного состояния вещества. Диэлектрические потерн могут обусловливаться сквозным током или, как указывалось при рассмотрении явления поляризации, активными составляющими токов смещения. В технических электроизоляционных материалах, помимо потерь от сквозной электропроводности и потерь от замедленной поляризации, возникают диэлектрические потери, которые сильно влияют на электрические свойства диэлектриков. Эти потери вызываются наличием изолированных друг от друга посторонних проводящих или полупроводящих включений углерода, оксидов железа; они значительны даже при малом содержании таких примесей в электроизоляционном материале. При высоких напряжениях потери в диэлектрике возникают вследствие ионизации газовых включений внутри диэлектрика» особенно интенсивно происходящей при высоких частотах. Дальнейшее рассмотрение диэлектрических материалов будем проводить на примере конденсатора. В любом реальном конденсаторе при работе его на переменном токе неизбежны потери в диэлектрике, обусловленные переменной поляризацией. Кроме того, конденсатор имеет ещё активную проводимость через изоляцию электродов, поэтому реальный конденсатор представляется эквивалентной схемой в виде идеальной ёмкости, последовательно или параллельно соединённой с активным сопротивлением (рисунок 2.2 а, б). Векторные диаграммы и схемы замещения для идеального диэлектрика и диэлектрика с потерями показаны на рисунке 2.2. Из векторной диаграммы тангенс этого угла равен отношению активного и реактивного токов или отношения активной мощности РА к реактивной РС.
Иногда для характеристики устройства с диэлектриком определяют добротность - параметр обратный тангенсу угла диэлектрических потерь:
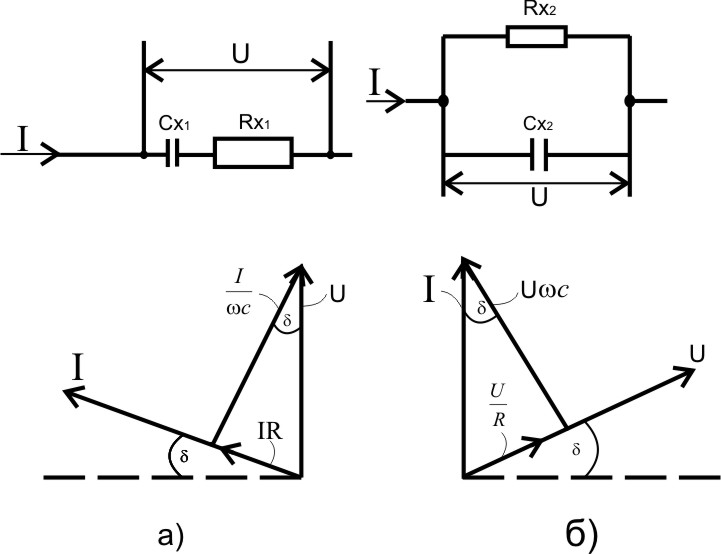 Рисунок 2.2– Последовательная (а) и параллельная (б) схемы замещения реального конденсатора и соответствующие векторные диаграммы Для последовательной схемы
для параллельной
Сопоставление формул для последовательной и параллельной схем замещения показывает, что они дают взаимно противоположные зависимости параметров цепи конденсатора от частоты. Это объясняется тем, что ни одна из схем замещения не отражает полностью тех реальных процессов, которые имеют место в конденсаторах. Последовательная схема и соответствующие ей формулы лучше отражают физические свойства реального конденсатора в области высоких частот (более 1 МГц), параллельная схема даёт более правильные результаты в области низких частот. В области средних частот обе схемы являются достаточно удовлетворительными. У материалов, применяемых на повышенных частотах и при высоких напряжениях, tgδ лежит в пределах 10-3 – 10-4; для низкочастотных диэлектрических материалов - полярных диэлектриков значения tgδ обычно 10-1 – 10-2, для слабополярных – до 10-3. Для хорошо осушенных газов, не содержащих влаги, значения могут достигать 10-5 – 10-8. Для упрощения расчетов часто пользуются комплексными величинами. Комплексная диэлектрическая проницаемость записывается в виде
где действительная часть ε' имеет физический смысл относительной диэлектрической проницаемости, а ε" характеризует потери
и называется коэффициентом диэлектрических потерь. Выбор в каждом конкретном случае той или иной эквивалентной схемы определяется значениями величин, подлежащих измерению. В некоторых случаях данная схема для удовлетворения условий равновесия нуждается в применении образцовых мер какого-либо необычного или неудобного номинального значения, например, очень больших или, наоборот, очень малых. Если объект измерения обладает малыми потерями, то при выборе параллельной эквивалентной схемы активное сопротивление составит несколько сотен килом, что явно неудобно. Последовательная схема в этом случае будет, несомненно, целесообразнее. Если же предполагается, что объект измерения обладает большими потерями, то используется параллельная эквивалентная схема. Поэтому, выбирая какую-либо схему, необходимо предварительно оценить порядок входящих в неё величин и параметров: если потери малы, то используется последовательная эквивалентная схема, если велики – то параллельная. Частотная зависимость потерь является важной характеристикой материала и определяется не только структурой материала, но и наличием и составом примесей. Как правило, потери имеют максимум при одной или нескольких частотах, в зависимости от строения диэлектрика. Положение максимумов на частотной оси характеризуется собственными частотами установления поляризации. Они могут быть связаны с поворотом полярных молекул в жидком диэлектрике или с поворотом домена в сегнетоэлектрике. При воздействии переменного напряжения, период которого много меньше времени установления соответствующей поляризации, диэлектрическая проницаемость и, соответственно, потери - малы. Поэтому в неполярных диэлектриках потери малы практически на всех частотах. Если период переменного напряжения близок к времени установления поляризации, то потери достигают максимального значения. Представим это на примере дипольной поляризации. При воздействии напряжения диполи начинают поворачиваться и ориентируются вдоль действия электрического поля примерно к моменту окончания первого полупериода напряжения. На следующем полупериоде они разворачиваются и ориентируются в новом направлении примерно к его окончанию. Это явление по своей сути напоминает резонанс. Получается, что диполи непрерывно вращаются, а поскольку этот процесс происходит в вязкой среде, то энергия движения, поступающая из электрического поля, передается окружающим молекулам. В результате этого энергия, поступающая из источника, расходуется на нагревание диэлектрика. При воздействии переменного напряжения, период которого много больше времени установления соответствующей поляризации, диэлектрическая проницаемость, соответствующая этому виду максимальна и потери, связанные с этим малы. Знание частотной зависимости tgδ необходимо для рационального выбора диэлектрика (или типа применяемого конденсатора), работающего при вполне определённых напряжениях и частотах, определяющих уровень диэлектрических потерь, а значит и температуру материала, которая не должна превышать предельно допустимую. Следует отметить, что влиянию температуры, частоты, влажности, напряженности поля подвержены не только диэлектрические потери, но и другие электрические характеристики диэлектриков – диэлектрическая проницаемость ε и проводимость γ. Причинами этого является зависимость характера движения связанных и свободных зарядов от этих факторов (рисунок 2.3). 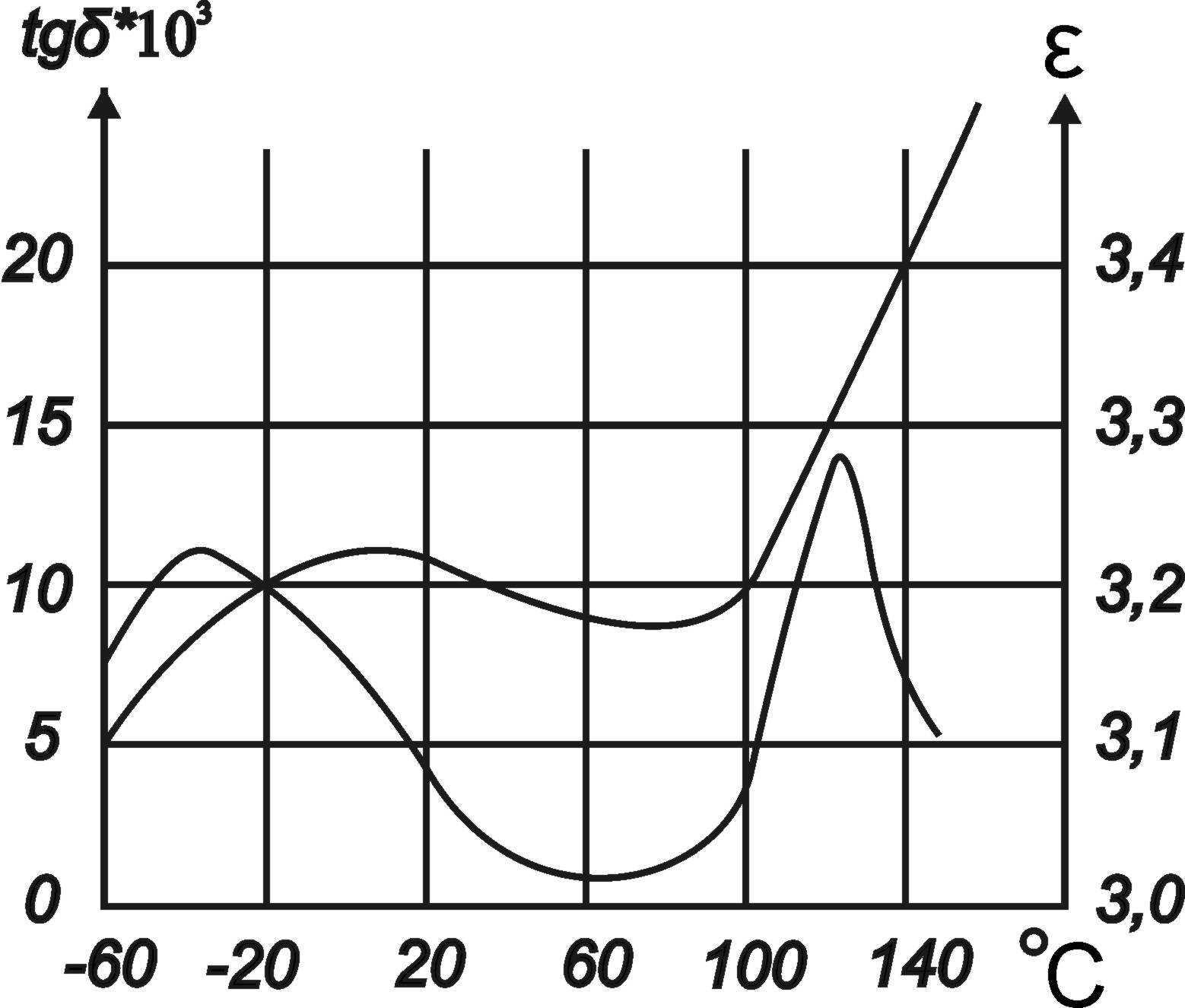 Рисунок 2.3– Зависимость угла диэлектрических потерь и диэлектрической проницаемости полиэтилентерефталатной плёнки от температуры |

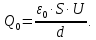
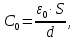
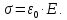
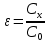
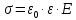 .
.