лаба 10. Лабораторная работа 1 конструкция зубчатого редуктора и проверка работоспособности основных его элементов

• Название: Лабораторная работа 1 конструкция зубчатого редуктора и проверка работоспособности основных его элементов
• Анкор: лаба 10
• Дата: 18.12.2022
• Размер: 256.49 Kb.
• Имя файла: Lab_rabota_1_Reduktor (1).docx
• Тип: Лабораторная работа; #851178
• страница: 1 из 4

Лабораторная работа № 1

КОНСТРУКЦИЯ ЗУБЧАТОГО РЕДУКТОРА И ПРОВЕРКА РАБОТОСПОСОБНОСТИ

ОСНОВНЫХ ЕГО ЭЛЕМЕНТОВ

1. Цель работы
Ознакомление с конструкцией зубчатого цилиндрического двухступенчатого редуктора и проверка работоспособности зубчатых передач, валов и подшипников опор валов редуктора при заданном режиме работы.
2. Задачи
1. Изучить конструкцию и принцип работы зубчатого редуктора.

2. Научиться методически грамотно выполнять проверочные расчеты зубчатых передач, валов и подшипников опор валов редуктора при заданном режиме работы.

3. Выработать умение анализировать полученные результаты расчетов и принимать конкретные решения по обеспечению работоспособности редуктора.
3. Краткие теоретические сведения
3.1. Критерии расчета зубчатых передач редуктора
Работоспособность зубчатых передач определяется выносливостью активных (рабочих) поверхностей зубьев и прочностью зубьев при изгибе.

При проверочных расчетах зубчатых передач на контактную выносливость проверяется условие предотвращения усталостного выкрашивания активных поверхностей зубьев, а при расчетах на контактную прочность при перегрузках – условие предотвращения остаточной деформации или хрупкого разрушения поверхностного слоя зубьев.

Основной целью проверочных расчетов на прочность зубьев при изгибе является проверка условий предотвращения усталостного излома зубьев (расчет на выносливость при изгибе), излома зубьев от малоцикловой усталости при плавном и ударном нагружении (расчет на малоцикловую выносливость при изгибе), остаточной деформации или хрупкого излома зубьев (расчет на прочность при изгибе максимальной нагрузкой).

В данной лабораторной работе выполняются только проверочный расчет зубчатых передач на контактную выносливость и расчет на выносливость при изгибе. В заданных условиях нагружения рассчитываемая передача обеспечивает заданный ресурс если выполняются условия _H ≤ [_H] и _F ≤ [_F]. Здесь _H и _F – расчетные значения соответственно контактного напряжения и напряжения изгиба зубьев; [_H] и [_F] – соответственно допускаемые контактные напряжения и допускаемые напряжения изгиба зубьев.

Расчетное контактное напряжение в полюсе зацепления цилиндрических косозубых колес определяют по формуле:

.

В указанную формулу входят следующие параметры:

T_1H – вращающий момент на шестерне, Нм;

E_пр – приведенный модуль упругости, МПа;

,

где E₁ и E₂ – модули упругости материала шестерни и колеса, для стальных зубчатых колес

E_пр = E_стали = 2,110⁵ МПа;

d_w1 – начальный диаметр шестерни, мм;

b_w – рабочая ширина зубчатого венца, мм;

_w – угол зацепления, в косозубых передачах чаще всего
_w =  = 20;

u – передаточное число ступени;

K_H – коэффициент расчетной нагрузки, в общем случае

K_H = K_Hβ  K_HV  K_H. (1.1)

Здесь: K_Hβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий; K_HV – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении; K_H – коэффициент, учитывающий распределение нагрузки между одновременно зацепляющимися зубьями.

Для оценки K_Hβ разработаны графики [1, рис. 8.15], по которым для заданной твердости зубьев колес, при соответствующем случае расположения колес относительно опор и относительной ширине зубчатого венца 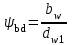, определяют величину коэффициента. Для приближенной оценки K_HV рекомендуют [1, табл. 8.3], где значение коэффициента выбирают по заданной степени точности (ГОСТ 1643-81), по твердости зубьев колес, по окружной скорости 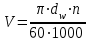и виду передачи (прямозубая или косозубая).

Величину K_H в расчетах рекомендовано назначить для 8-й степени точности и окружной скорости колес V  5 м/с равной 1,07.

Z_Hβ – коэффициент повышения прочности косозубых передач по контактным напряжениям, его рассчитывают по формуле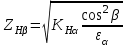

, (1.2)

где β – угол наклона зубьев;

_– коэффициент торцового перекрытия зубчатой передачи
z₁ – z₂,

. (1.3)

Расчетное местное напряжение при изгибе зубьев определяют по формуле

.

Здесь: F_tF – окружная сила, , Н;

K_F – коэффициент нагрузки при расчете на изгиб,

K_F = K_Fβ  K_FV  K_F, (1.4)

где K_Fβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий; K_FV – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении;
K_F – коэффициент, учитывающий распределение нагрузки между одновременно зацепляющимися зубьями.

Значение коэффициента K_Fβ определяют по графикам [1,
рис. 8.15] с учетом твердости зубьев, схемы расположения колес относительно опор и относительной ширины зубчатого венца колес _bd. Величину K_FV определяют по [1, табл. 8.3] для заданной точности зубчатых колес, твердости материала колес, окружной скорости и вида передачи. Коэффициент K_F рекомендовано принять равным 1,22 для 8-й степени точности колес при окружной скорости
V  5 м/с.

Y_FS – коэффициент, учитывающий форму зуба и концентрацию напряжений; его значение определяют по [1, рис. 8.20] для числа зубьев эквивалентного прямозубого колеса .
Допускаемые контактные напряжения определяют раздельно для шестерни и колеса по формуле

, (1.5)

где _Hlim – предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов перемены напряжений, МПа. Величину предела определяют по [1, табл. 8.8] в зависимости от вида термообработки и марки стали.

S_H – коэффициент безопасности; рекомендовано [1] назначать
S_H = 1,1 при нормализации, термоулучшении и объемной закалке,
S_H = 1,2 при поверхностной закалке, цементации и азотировании;

Z_N – коэффициент долговечности, учитывает влияние срока службы и режима нагрузки передачи.

– при постоянном режиме нагрузки

и

– при переменных режимах нагрузки передачи.

Следует принимать ограничение Z_{N max} ≤ 2,6 при S_H = 1,1 и
Z_{N max} ≤ 1,8 при S_H = 1,2 .

Здесь: N_HG – базовое число циклов перемены напряжений, рассчитываемое по формуле

,

где HB_ср – среднее значение твердости в единицах Бринелля;

N_K – общее число циклов перемены напряжений,
N_K = 60  n t,

n – частота вращения зубчатого колеса, об/мин;

t – суммарный срок службы передачи, час;

N_HE – эквивалентное число циклов перемен напряжений при расчете контактной выносливости, при наличии циклограммы нагрузки его рассчитывают по формуле

,

где T_i – вращающие моменты при переменном режиме нагрузки, действующие в течение t_i отрезка времени. Принято, что n = const.

В случае задания типового режима нагружения эквивалентное число циклов рассчитывают по формуле

.

Здесь: _H – коэффициент эквивалентности, его значение определяют по [1, табл. 8.9] для заданного режима работы.

В качестве допускаемого контактного напряжения в передаче принимают:

– для прямозубых и косозубых цилиндрических передач с небольшой разностью твердостей зубьев колес меньшее из двух допускаемых напряжений, определенных для шестерни и колеса, т.е.

;

– для косозубых передач со значительной разностью твердостей (H₁ – H₂  70…80 НВ)

.
Допускаемое напряжение изгиба при расчете зубьев на выносливость определяют по формуле

, (1.6)

где _{F lim} – предел выносливости зубьев по напряжениям изгиба, МПа; S_F – коэффициент безопасности.

Значения S_F определяют по [1, табл. 8.8] в зависимости от вида термической обработки;

Y_N – коэффициент долговечности, его рассчитывают по формуле

– при постоянном режиме нагрузки

и

– при переменном режиме нагрузки.

Здесь m_F = 6 – для материалов колес с твердостью НВ 350, а также со шлифованной переходной поверхностью зубьев, при этом
Y_{N max} ≤ 4; и m_F = 9 – для зубчатых колес с Н  350 НВ и нешлифованной поверхностью при максимальном значении Y_{N max} ≤ 2,5;

N_FE – эквивалентное число циклов перемен напряжений при изгибе,

.

Здесь принято n = const.

При использовании типового режима нагружения

,

где _F – коэффициент эквивалентности, его значение принимают по [1, табл. 8.9];

Y_A – коэффициент, учитывающий влияние двухстороннего приложения нагрузки; Y_A = 1 при односторонней нагрузке и
Y_A = 0,7…0,8 – при реверсивной.
3.2. Критерии расчета валов передач редуктора
При работе редуктора под нагрузкой его валы испытывают в основном действие напряжений изгиба и кручения. Постоянные по направлению силы в зацеплении вызывают в поперечных сечениях валов нормальные напряжения, изменяющиеся по знакопеременному симметричному циклу, а передаваемые валами вращающие моменты – касательные напряжения кручения, изменяющиеся по отнулевому циклу.

На практике установлено, что для редукторных валов основным видом разрушения является усталостное, а основным расчетом – расчет на сопротивление усталости.

Расчет обычно производят в форме проверки коэффициента запаса прочности по выносливости в опасном сечении вала

.

Здесь s_, s_ – коэффициент запаса прочности соответственно по нормальным (изгиба) и касательным (кручения) напряжениям;

и .

В этих формулах:

_–1, _–1 – пределы выносливости материала вала при симметричном цикле; приближенно принимают _–1 = (0,4…0,5)_в и _–1 = (0,2…0,3)_в;

_a = _и – амплитуда переменной составляющей циклов напряжений (или напряжения изгиба ) в проверяемом сечении вала, для определения величины напряжений обычно строят эпюры изгибающих моментов;

_m – постоянная составляющая цикла напряжений, ввиду малости её величины, обычно принимают _m = 0;

– напряжения кручения, , t – вращающий момент на валу;

_, _ – коэффициенты, корректирующие влияние постоянной составляющей цикла напряжений на сопротивление усталости. Величины _ и _ зависят от механических характеристик материала, рекомендуют [1] принимать _ = 0,02 + 210^–4  _в, _ = 0,5  _;

K_D, K_D – коэффициенты концентрации напряжений соответственно при изгибе и при кручении в проверяемом сечении, их рассчитывают по формулам:

и .

Здесь: K_, K_ – эффективные коэффициенты концентрации напряжений;

K_d, K_d – коэффициенты, учитывающие размеры поперечного сечения вала;

K_F, K_F – коэффициенты, учитывающие качество (шероховатость) поверхности;

K_V – коэффициент влияния упрочнения, вводимый для валов с поверхностным упрочнением.

Значения всех указанных коэффициентов определяют по [1, табл. 15.1…15.4].
3.3. Критерии проверки подшипников опор валов
В настоящее время наиболее распространены опоры валов редукторов на подшипниках качения. Современный расчет подшипников качения базируется на двух критериях: 1) расчете на статическую грузоподъемность по предотвращению остаточных деформаций при действии кратковременных перегрузок и весьма малых частотах вращения валов; 2) расчете на долговечность (ресурс работы) по динамической грузоподъемности, ограничивающей усталостное выкрашивание рабочих поверхностей деталей подшипника.

Динамическая грузоподъемность C и ресурс L_h (час) подшипника качения связаны следующими зависимостями:

или . (1.7)

Здесь: a₁ – коэффициент долговечности;

a₂₃ – обобщенный коэффициент совместного влияния качества металла, особенностей технологии производства, конструкции и условий эксплуатации;

p – показатель степени, для шарикоподшипников p = 3, а для роликоподшипников p = 10 / 3;

n – частота вращения вала, об/мин;

p_r – эквивалентная динамическая радиальная нагрузка, Н,

, (1.8)

где F_R, F_A – соответственно радиальная реакция опоры и осевая нагрузка на подшипник, при этом осевая сила должна алгебраически складываться из осевых составляющих F_a в зацеплениях обеих ступеней редуктора;

X, Y – коэффициенты, учитывающие разное повреждающее действие радиальной и осевой нагрузок;

V – коэффициент вращения, зависящий от того, какое кольцо подшипника вращается при работе под нагрузкой, V = 1 – в случае вращения внутреннего кольца относительно внешней нагрузки;

K_Б – коэффициент безопасности, учитывающий характер нагрузки на подшипник;

K_t – температурный коэффициент, вводимый только при повышенной рабочей температуре подшипникового узла (t  100 С).

Рекомендации по назначению величин перечисленных коэффициентов приведены в [1, табл. 16.3 и 16.5].

Подшипники, работающие при переменных режимах нагрузки, проверяют по эквивалентной нагрузке, вызывающей такой же эффект усталостного разрушения, что и весь комплекс действующих на механизм нагрузок. В этом случае эквивалентную нагрузку удобно рассчитывать по следующей зависимости:

, (1.9)

где T_i, T_max, L_i, L – параметры циклограммы нагружения.

Расчет упрощается, если задан типовой режим нагружения. В этом случае эквивалентная радиальная нагрузка

, (1.10)

где P_r – определяют по максимальной из длительно действующих нагрузок;

K_E – коэффициент эквивалентности, его значение принимают в зависимости от режима нагрузки по таблице:

Типовой режим нагрузки	0	I	II	III	IV	V
KE	1	0,8	0,63	0,56	0,5	0,4

Теперь номинальная долговечность (ресурс) подшипника в часах

. (1.11)