Хар. Котлов. Лабораторная работа 1 определение вязкости жидкости цель работы
 Скачать 32.93 Kb. Скачать 32.93 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА №1 ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ Цель работы: определить динамическую и кинематическую вязкости жидкости методом Стокса (метод падающего шарика). Приборы и принадлежности: цилиндрический сосуд с исследуемой жидкостью, штангенциркуль, секундомер, масштабная линейка, шарики. Общие сведения Вязкость - важная физико-химическая характеристика веществ. Величина, обратная вязкости, называется текучестью. Её необходимо учитывать, например, при перекачке жидкостей и газов по трубопроводам, разливке расплавленных металлов, смазке машин и механизмов. В медицине вязкость крови определяет состояние организма - в норме или при патологии. Динамическая вязкость – характеристика вещества, численно равная силе трения, возникающей между двумя слоями жидкости площадью по 1 м2 каждый при градиенте скорости, равном 1м/с на метр. Размерность динамической вязкости (µ)=(Па*с). В некоторых случаях принято пользоваться так называемой кинематической вязкостью, равной динамической вязкости жидкости, деленной на плотность жидкости, м2/с: ν=µ/ρ Описание лабораторной установкой Для определения вязкости жидкости по методу Стокса берётся высокий цилиндрический сосуд с исследуемой жидкостью (рис. 1). На сосуде имеются две кольцевые метки А и В, расположенные на расстоянии lдруг от друга. Расстояние между метками можно изменять. Уровень жидкости должен быть выше верхней метки на l0 = 4...5 см, чтобы к моменту прохождения шарика мимо верхней метки его скорость можно было считать установившейся. Бросая шарик в сосуд, отмечают по секундомеру время tпрохождения шариком расстояния l = АВ между двумя метками. Вязкость определяется по следующей формуле: 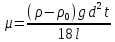 (1) (1)У 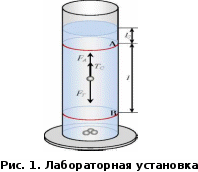 равнение (1) справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки радиусом R0, то приходится учитывать влияние боковых стенок. Поправки в формуле Стокса для такого случая теоретически обосновал Ладенбург. равнение (1) справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки радиусом R0, то приходится учитывать влияние боковых стенок. Поправки в формуле Стокса для такого случая теоретически обосновал Ладенбург.При падении шарика радиусом r в цилиндрической трубе радиусом R0, высотой учет влияния границ дает: 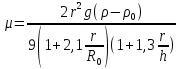 (2) (2)Таким образом, зная плотности материала шарика и жидкости, радиусы шарика и сосуда, скорость установившегося движения шарика, по формуле (2) можно вычислить динамическую вязкость жидкости. Порядок выполнения работы: 1. Взять данные по плотности материала шарика р и исследуемой жидкости р0 (при необходимости измерить плотность жидкости с помощью ареометра). Занести полученные данные в табл. 1. 2.Установить расстояние от уровня жидкости до верхней метки l0 не менее 40 мм, а расстояние между метками l= 200...400 мм. Измерить внутренний радиус сосуда Ro и расстояние между метками на сосуде. Все измеренные данные записать в табл. 1. 3. Отобрать 10 шариков. Измерить диаметры шариков dс помощью штангенциркуля. Результаты измерений занести в табл. 2. 4.Отпустить один шарик в цилиндр с жидкостью, как можно ближе к его оси (в случае образования пузырьков воздуха на поверхности шарика необходимо взять другой шарик и повторить данный опыт). В момент прохождения шарика мимо верхней метки включить секундомер и остановить его в момент прохождения шариком нижней метки. В процессе наблюдения за шариком, в момент прохождения им метки, глаз должен находиться на одном уровне с меткой. Результаты измерения времени занести в табл. 2. 5. Повторить эксперимент с остальными шариками. Результаты измерений времени падения шариков между метками с точностью до 0,2 с занести в табл. 2. Таблица 1. Данные по лабораторной установке исследуемой жидкости
Таблица 2. Опытные данные и результаты расчета вязкости
Контрольные вопросы 1.Что характеризуют динамическая и кинематическая вязкости? 2. Как зависят от температуры вязкости большинства жидкостей? 3. Какой безразмерный комплекс определяет характер обтекания твёрдого тела жидкостью? 4. Напишите и поясните выражение для силы Стокса и силы Архимеда. 5. Какие силы действуют на шарик, падающий в вязкой жидкости? Как эти силы связаны между собой в случае установившегося движения? 6. Почему из расчётов следует исключить данные, полученные в случае падения шарика с прилипшими к нему пузырьками воздуха? 7. Влияют ли размеры сосуда, в котором находится жидкость, на величину силы сопротивления трению, действующей на тело, движущееся в этой жидкости? Если да, то почему? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

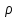
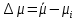
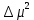
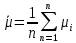 , Па*с
, Па*с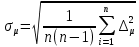
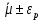 , Па*с
, Па*с